递归和栈

原文链接：http://javascript.info/recursion，translate with ❤️ by zhangbao.

我们回到函数，来更加深入的学习。

我们的第一个话题是递归。

如果你不是编程新手，相比对递归已经不陌生了，大可跳过此章。

递归是一种编程模式，当任务可以自然地分成几个相同类型的任务时，它是非常有用，而且简单。或者当一个任务可以被简化为一个简单的动作，再加上一个简单的相同任务的变体。或者，我们很快就会看到，去处理某些特定的数据结构。

当一个函数解决一个任务时，在这个过程中它可以调用许多其他函数。一个特殊的情况是，当一个函数调用自己，这就是所谓的递归。

两种思考方式

为了简单开始，我们写一个简单函数 pow(x, n) 返回 x 的 n 次幂。也就是说，x 跟自己相乘 n 次数。

pow(2, 2) = 4
pow(2, 3) = 8
pow(2, 4) = 16

有两种实现它的方式。

1. 一种：使用 for 循环

function pow(x, n) {
    let result = 1;
    // 在循环里使用 x 与自己相乘 n 次
    for (let i = 0; i < n; i++) {
        result *= x;
    }
    return result;
}
alert( pow(2, 3) ); // 8

1. 使用递归，自己调用自己：

function pow(x, n) {
    if (n === 1) {
        return  x;
    } else {
        return x * pow(x, n - 1);
    }
}
alert( pow(2, 3) ); // 8

请注意递归变量是如何从根本上不同的。

当 pow(x, n) 被调用时，执行被分成两个分支：

              if n==1  = x
             /
pow(x, n) =
             \
              else     = x * pow(x, n - 1)

1. 如果 n === 1，一切就变得不重要了。它称为基本递归，因为它会直接返回结果：pow(x, 1) 等于 x，

2. 否则，我们用 x pow(x, n-1) 来表示 pow(x, n)，用数学表示就是 x= x * pow(x, n - 1)。这称为递归步骤：我们将任务转换为一个更简单的操作（乘以 x）和一个更简单的相同任务的调用（pow 与低 n）。接下来的步骤将进一步简化，直到 n 达到 1。

我们也可以说 pow 递归地调用自己直到 n == 1。

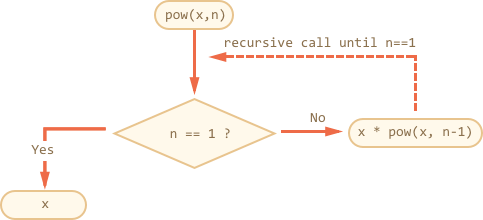
例如，要计算 pow(2, 4) 会执行以下的递归步骤：

1. pow(2, 4) = 2 * pow(2, 3)

2. pow(2, 3) = 2 * pow(2, 2)

3. pow(2, 2) = 2 * pow(2, 1)

4. pow(2, 1) = 2

因此，递归将一个函数降级调用成更简单的函数，然后——甚至更简单，等等，直到结果变得显而易见。

注：递归的写法通常更短

递归解决方案通常比迭代的解决方案要短。

这里我们可以用三目运算符 ? 而不是 if 去重写 pow(x, n)，写法就会更简洁，而且可读性更强：

function pow(x, n) {
  return (n == 1) ? x : (x * pow(x, n - 1));
}

嵌套调用的最大数量（包括第一个调用）称为递归深度。在我们的例子中，它正好是 n。

最大的递归深度受到 JavaScript 引擎的限制。我们可以确定大约是 10000 个，个别引擎允许更多，但是100000 可能超出了大多数的限制。有一些自动优化可以帮助缓解这种情况（“尾部调用优化”），但是它的支持程度不够好，并且只在简单的情况下生效。

这限制了递归的应用，但它仍然非常广泛。在许多任务中，递归的思维方式提供了更简单的代码，更易于维护。

执行栈

现在，让我们研究递归调用是如何工作的。为此，我们将研究函数底层的调用。

函数执行时的信息存储在它的执行环境中。

执行环境是一个内部数据结构，包含函数执行的详情信息：现在的控制流在哪里了，当前的变量，this 的值（这里没有使用）还有少数其他的一些内部详情。

一个函数调用恰好有一个与之相关联的执行上下文。

当一个函数进行嵌套调用时，会发生以下情况：

• 当前函数暂停，

• 与之关联的执行环境被记忆在一个特殊的数据结构里，称为执行环境栈，

• 嵌套调用执行，

• 结束后，旧的执行环境从栈中取回，外部函数从它之前停止的地方恢复。

我们来看看，在 pow(2, 3) 调用期间发生了什么。

pow(2, 3)

在刚开始调用 pow(2, 3) 执行环境会存储变量：x=2, n = 3，函数执行到第 1 行的时候：

开始开始执行，条件 n === 1 不成立，所以控制流进入到第二个 if 分支：

function pow(x, n) {
  if (n == 1) {
    return x;
  } else {
    return x * pow(x, n - 1);
  }
}
alert( pow(2, 3) );

变量还是一样的，但是当前执行的行数变了，环境现在是：

计算 x * pow(x, n - 1)，我们需要开始子调用 pow，使用新参数 pow(2, 2)。

pow(2, 2)

在子调用中，JavaScript 记住当前执行环境到执行环境栈里。

这里我们调用了相同的函数 pow，但是这完全不重要。所有函数的处理过程都是一样的：

1. 当前的执行环境被“记忆”在栈顶部，

2. 为子调用创建新的环境，

3. 当子调用完成调用，前一个从栈中弹出，继续开始它的执行。

当我们进入到子调用 pow(2, 2) 时的环境栈情况：

新的当前执行上下文位于顶部（用粗体标识），之前记忆的上下文就在下面了。

当我们结束了子调用时，恢复以前的上下文很容易，因为它同时保留了两个变量和它停止的代码的确切位置。在图中我们使用了“line”这个词，当然它更精确。

pow(2, 1)

处理流程开始重复了：在第 5 行，一个新的子调用开始了，携带参数 x=2, n = 1。

一个新的执行环境被创建，之前的环境推进到栈顶：

这里以后 2 个旧的环境，和 1 各当前正在执行的 pow(2, 1)。

退出

pow(2, 1) 的执行，不像之前的，条件 n === 1 为真的了，所以第一个分支 if 语句执行了：

function pow(x, n) {
  if (n == 1) {
    return x;
  } else {
    return x * pow(x, n - 1);
  }
}

没有更多的嵌套调用，所以函数结束，返回 2。

函数完成之后，它的执行环境再也不需要了，于是就从内存中清除了。之前环境现在到了栈顶部：

pow(2, 2) 的执行恢复了。现在得到了 pow(2, 1) 执行返回的结果，因此 x * pow(x, n - 1) 也能返回结果，返回 4 了。

之前的环境恢复了：

执行结束后，我们得到 pow(2, 3) 返回的结果，8。

这个例子的递归深度是 3。

正如我们从上面的插图中看到的，递归深度等于堆栈中最大的上下文环境的数量。

注意内存需求，上下文环境占据内存空间。在我们的例子中，请一个数的 n 次幂实际上需要 n 个上下文环境的内存，对于所有较低的 n 值。

基于循环的算法更节省内存：

function pow(x, n) {
  let result = 1;
  for (let i = 0; i < n; i++) {
    result *= x;
  }
  return result;
}

迭代 pow 使用单一上下文环境，整个过程里改变 i 和 result 的值，它的内存需求小，且固定，不依赖于 n。

任何递归都可以重写为一个循环，循环变体通常可以变得更有效。

但是有时候重写起来不简单，特别是当需要依赖条件判断去合并结果，然后函数使用不同的递归子调用时，这种会有复杂分支情况的时候。这种优化可能是不需要的，完全不值得付出努力。

递归可以提供更短的代码，更容易理解和支持。并不是每个地方都需要优化，大多数情况下我们需要一个已读的好代码，这就是使用递归的原因。

递归遍历

递归的另一个伟大应用是递归遍历。

想象一下，我们有一家公司。员工结构可以用一个对象表示：

let company = {
  sales: [{
    name: 'John',
    salary: 1000
  }, {
    name: 'Alice',
    salary: 600
  }],
  development: {
    sites: [{
      name: 'Peter',
      salary: 2000
    }, {
      name: 'Alex',
      salary: 1800
    }],
    internals: [{
      name: 'Jack',
      salary: 1300
    }]
  }
};

也就是说，公司里有部门：

• 部门是一个包含员工的数组。例如，sales 部门有两个雇员：John 和 Alice。

• 或者一个部门可以分成多个小部门，像 development 有两个部门：sites 和 internals。每个子部门也有自己的雇员。

• 有可能一个部门增长了，然后分解成多个子部门（或者团队）。

例如，sites 部门未来分化成了 siteA 和 siteB 两个团队。而且，他们可能会分裂得更多。这没有显示在照片上，只是我们想象的东西。

现在，现在假设我们想要一个函数来得到所有工资的总和。我们怎么做呢？

迭代的方法并不容易，因为结构不是简单的。第一个想法可能是在第一个级别的部门中对带有嵌套子循环的 company 进行 for 循环。但是，我们需要更多的嵌套子循环来迭代像站点这样的二级部门的人员。然后是另一个在未来可能出现的第三级部门的子循环？我们应该停在 3 级还是 4 级的循环？如果我们在代码中放入 3-4 个嵌套的子循环来遍历单个对象，那么它就变得相当难看了。

我们来试试递归。

正如我们所看到的，当我们的函数在求一个部门的工资总和，有两种可能的情况：

1. 要不然它是个简单的部门，一个数组里就是所有的雇工——我们可以在一个很简单的循环里获得工资总和。

2. 或者是一个包含 N 个子部门的大部门——我们可以 N 此递归调用，先得到各子部门的工资总和，然后在将结果都加起来。

(1) 是递归的基础，是基本情况。

(2) 是递归步骤。一个复杂的任务被划分为小部门的子任务。它们可能会再次分裂，但迟早会结束在 (1)。

该算法可能更容易从代码中读取：

let company = { // the same object, compressed for brevity
  sales: [{name: 'John', salary: 1000}, {name: 'Alice', salary: 600 }],
  development: {
    sites: [{name: 'Peter', salary: 2000}, {name: 'Alex', salary: 1800 }],
    internals: [{name: 'Jack', salary: 1300}]
  }
};
function sumSalaries(department) {
  if (Array.isArray(department)) { // case (1)
    return department.reduce((prev, current) => prev + current.salary, 0); // sum the array
  } else { // case (2)
    let sum = 0;
    for (let subdep of Object.values(department)) {
      sum += sumSalaries(subdep); // recursively call for subdepartments, sum the results
    }
    return sum;
}
alert(sumSalaries(company)); // 6700

代码很短，很容易理解（希望如此？）这就是递归的力量。它也适用于任何级别的子部门嵌套。

这是调用过程的图表表示：

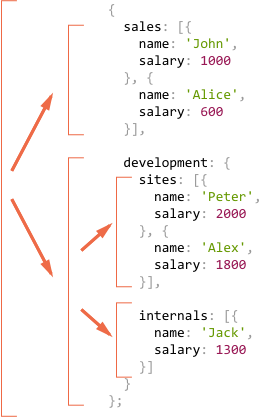
我们可以很容易地看到这个原理：对于一个对象 {…} 会创建子调用，而数组 […] 是递归树上的“叶子”节点，它们会立即产生结果。

注意，代码使用了我们之前介绍过的智能特性：

• arr.reduce 方法是数组方法一章里介绍的用来得到数组总和的。

• 循环 for (val of Object.values(obj)) 去迭代对象值：Object.values() 返回对象的属性值集合。

递归结构

递归（递归定义的）数据结构是一个在各个部分复制自身的结构。

我们刚刚在上面的公司结构的例子中看到过。

一个公司的部门：

1. 是有雇员们组成的一个数组，

2. 或者是一个包含子部门的对象。

对于 Web 开发人员来说，有许多更广为人知的例子：HTML 和 XML 文档。

在 HTML 文档中，HTML-tag 可能包含以下列表：

1. 文本片段

2. HTML 注释

3. 其他 HTML 标签（反过来可能包含文本片段/评论或其他标签等）。

这又是一个递归定义。

为了更好地理解，我们将介绍一个名为“链表”的递归结构，在某些情况下，这可能是数组的一个更好的选择。

链表

想象一下，我们想要存储一个有序的对象列表。

自然选择是一个数组：

let arr = [obj1, obj2, obj3];

但是数组有一个问题。“删除元素”和“插入元素”操作是昂贵的。例如，arr.unshift(obj) 操作必须重新编号所有元素，为新的 obj 腾出空间，如果数组很大，则需要时间。arr.shift() 方法也是一样。

唯一不需要大规模重新设计的结构修改是那些在数组末尾运行的：arr.push/pop。因此，对于大队列来说，数组可能相当慢。

或者，如果我们真的需要快速插入/删除，我们可以选择另一个称为链表的数据结构。

链表元素递归地定义为一个对象：

• value

• next 属性引用下一个链表元素，如果是链表上的末尾元素的话，next 属性值就是 null。

例如：

let list = {
  value: 1,
  next: {
    value: 2,
    next: {
      value: 3,
      next: {
        value: 4,
        next: null
      }
    }
  }
};

这条链表用图表示是这样的：

创建的另一种代码：

let list = { value: 1 };
list.next = { value: 2 };
list.next.next = { value: 3 };
list.next.next.next = { value: 4 };

在这里，我们可以更清楚地看到有多个对象，每个对象都有值，然后指向邻居。list 变量是链条中的第一个对象，因此在接下来的指针中，我们可以到达任何元素。

这个列表可以很容易地分成多个部分，然后再加入：

let secondList = list.next.next;
list.next.next = null;

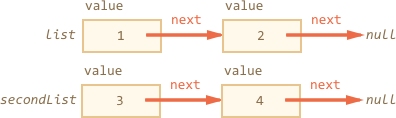
连接：

list.next.next = secondList;

当然，我们可以在任何地方插入或删除物品。

例如，为了获得一个新值，我们需要更新列表的头部：

let list = { value: 1 };
list.next = { value: 2 };
list.next.next = { value: 3 };
list.next.next.next = { value: 4 };
// prepend the new value to the list
list = { value: "new item", next: list };

要从中间删除一个值，改变前面的一个值：

list.next = list.next.next;

我们做了列表，下一个跳过 1 到值 2。值 1 现在被排除在链之外。如果它没有存储在其他地方，它将自动从内存中删除。

不像数组，没有大规模的重新排列，我们可以很容易地重新排列元素。

当然，列表并不总是比数组更好。否则，每个人都只使用列表。

主要的缺点是我们不能通过它的数字轻易地访问一个元素。在一个简单的数组中：arr[n] 是一个直接引用。但是在列表中，我们需要从第一项开始，然后到 N 次，得到第 N 个元素。

但是我们并不总是需要这样的操作。例如，当我们需要一个队列甚至一个 deque 时——有序的结构必须允许从两端快速添加/删除元素。

有时，添加另一个名为 tail 的变量来跟踪列表的最后一个元素是值得的（并在添加/删除元素的时候更新它）。对于大量的元素，速度差异和数组是巨大的。

总结

术语：

• 递归是一个编程术语，意思是“自调用”函数。这样的功能可以用优雅的方式来解决某些任务。

当一个函数调用自己时，它被称为递归步骤。递归的基础是函数参数，使任务变得简单，以至于函数不会进行进一步调用。

• 递归定义的数据结构是可以用自身定义的数据结构。

例如，链表可以定义为一个数据结构，由引用列表（或null）的对象组成。

list = { value, next -> list }

像 HTML 元素树或者这一章的树状树，也自然递归：它们分支，每个分支都可以有其他分支。

递归函数可以像我们在 sum 工资示例中看到的那样使用递归函数。

任何递归函数都可以被重写为迭代的函数。这有时需要优化一些东西。但是对于许多任务来说，递归解决方案的速度足够快，并且更容易编写和支持。

(完)