- 1.1 训练,验证,测试集(Train / Dev / Test sets)
- 1.2 偏差,方差(Bias /Variance)
- 1.3 机器学习基础(Basic Recipe for Machine Learning)
- 1.4 正则化(Regularization)
- 1.5 为 什 么 正 则 化 有 利 于 预 防 过 拟 合 呢 ? ( Why regularization reduces overfitting?)
- 1.6 dropout 正则化(Dropout Regularization)
- 1.7 理解 dropout (Understanding Dropout)
- 1.8 其他正则化方法(Other regularization methods)
- 1.9 归一化输入(Normalizing inputs)
- 1.10 梯度消失/ 梯度爆炸(Vanishing / Exploding gradients)
- 1.11 神经网络的权重初始化(Weight Initialization for Deep Networks)
- 1.12 梯度的数值逼近(Numerical approximation of gradients)
- 1.13 梯度检验(Gradient checking)
- 1.14 梯 度 检 验 应 用 的 注 意 事 项 ( Gradient Checking Implementation Notes)
tags: [笔记, 吴恩达深度学习, 第一周:深度学习的实践层面]
categories: [笔记, 吴恩达深度学习, 第一周:深度学习的实践层面]
1.1 训练,验证,测试集(Train / Dev / Test sets)
注意划分比例
小数据集:按70/30/0;60/20/20比例划分比较合理
大规模数据集(百万条):则按98/1/1;99.5/0.25/0.25;99.5/0.4/0.1比例划分才合理
1.2 偏差,方差(Bias /Variance)
通过比较训练集误差(Train set error)和验证集误差(Dev set error)的情况,来确定模型是具有高偏差(欠拟合)、高方差(过拟合)、既高偏差又高方差、低偏差低方差(好的模型)。
注:偏差误差是相对的,若原本数据误差就很高,训练出的模型误差高也很合理
1.3 机器学习基础(Basic Recipe for Machine Learning)
1、解决偏差高的方法(评估训练集或训练数据的性能):甚至选择一个新的网络(用规模更大的网络)通常可以很好的拟合训练集,比如含有更多隐藏层或者隐藏单元的网络;或者花费更多时间来训练网络(不一定有用,但也没什么坏处),或者尝试更先进的优化算法。
2、解决偏差问题后,再查看模型方差(查看验证集性能):最好的解决办法就是采用更多数据;,但有时候,我们无法获得更多数据,我们也可以尝试通过正则化来减少过拟合,
总结:总之就是不断重复尝试,直到找到一个低偏差,低方差的框架,这时你就成功了。
1.4 正则化(Regularization)
正则化方法:L1正则化,L2正则化(或称权重衰减,或“弗罗贝尼乌斯范数”), dropout 正则化
1.5 为 什 么 正 则 化 有 利 于 预 防 过 拟 合 呢 ? ( Why regularization reduces overfitting?)
如果正则化参数变得很大,参数W很小,z也会相对变小,此时忽略b的影响,z会相对变小,实际上,z的取值范围很小,这个激活函数,也就是曲线函数tanh会相对呈线性,整个神经网络会计算离线性函数近的值,这个线性函数非常简单,并不是一个极复杂的高度非线性函数,不会发生过拟合。
1.6 dropout 正则化(Dropout Regularization)
“Dropout(随机失活)”原理:保留一类节点集合,删除其它类型的节点集合。
实施 dropout 最常用的方法就是 Inverted dropout(反向随机失活),前向传播、后向传播中都可以实施。
1.7 理解 dropout (Understanding Dropout)
dropout将产生收缩权重的平方范数的效果,和之前讲的L2正则化类似;
实施 dropout 的另一个细节是,这是一个拥有三个输入特征的网络,其中一个要选择的参数是 keep-prob,它代表每一层上保留单元的概率。所以不同层的 keep-prob 也可以变化。
1.8 其他正则化方法(Other regularization methods)
一.数据扩增(Data augmentation)
通过人工合成的方法伪造扩增训练数据来解决过拟合问题。
二.提早停止(early stopping)
验证集误差通常会先呈下降趋势,然后在某个节点处开始上升,early stopping 的作用是,当神经网络已经在这个迭代过程中表现得很好时,就在此停止训练。
所以 early stopping 要做就是在中间点停止迭代过程,我们得到一个w值中等大小的弗罗贝尼乌斯范数,与L2正则化相似,选择参数w范数较小的神经网络,但愿你的神经网络过度拟合不严重。
early stopping缺点:不能独立地处理优化代价函数J和防止过拟合(方差高)这两个问题,因为提早停止梯度下降,也就是停止了优化代价函数𝐾,因为现在你不再尝试降低代价函数J,所以代价函数J的值可能不够小,同时你又希望不出现过拟合,你没有采取不同的方式来解决这两个问题,而是用一种方法同时解决两个问题,这样做的结果是我要考虑的东西变得更复杂。
Early stopping 优点:只运行一次梯度下降,你可以找出w的较小值,中间值和较大
值,而无需尝试L2正则化超级参数λ的很多值。
优化算法:主要是用来优化代价函数J,比如梯度下降,Momentum,RMSprop 和 Adam 等等。重点优化代价函数J时,只需要留意w和b,J(w,b)的值越小越好。
1.9 归一化输入(Normalizing inputs)
若数据的各特征数值范围差距较大,尝试归一化数据,提高模型的训练速度。
1.10 梯度消失/ 梯度爆炸(Vanishing / Exploding gradients)
如果激活函数或梯度函数以与L相关的指数增长或递减,它们的值将会变得极大或极小,从而导致训练难度上升,尤其是梯度指数小于L时,梯度下降算法的步长会非常非常小,梯度下降算法将花费很长时间来学习。
1.11 神经网络的权重初始化(Weight Initialization for Deep Networks)
Relu 激活函数: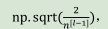
tanh 函数: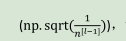
另一种方法: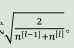
1.12 梯度的数值逼近(Numerical approximation of gradients)
使用双边误差公式来求函数𝑔的偏导
1.13 梯度检验(Gradient checking)
在后向传播时进行梯度检验,判断算法是否有bug,即dθ与dθapprox两个向量是否相近。如下图所示方法进行计算: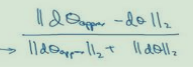
1.14 梯 度 检 验 应 用 的 注 意 事 项 ( Gradient Checking Implementation Notes)


