tags: [笔记, Numpy, 矩阵运算]
categories: [笔记, Numpy, 矩阵运算]

开始之前

机器学习中的损失函数：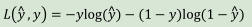
代码实现：

logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
loss = 1./m * np.nansum(logprobs)

numpy中array和matrix的区别：

matrix是array的分支，matrix和array操作在多数情况下都是一样的，但array操作更灵活，速度更快。

创建矩阵或数组

import numpy as np
a = np.array([2,3,4])
print(a)
print(a.shape,a.ndim,a.dtype,a.dtype.name,a.itemsize,a.size,a.data)
b = np.arange(12).reshape(4,3)
b
m = np.asmatrix(b)
type(m)

[2 3 4]
'int32'
(3,) 1 int32 int32 4 3 <memory at 0x000001AF30C23348>
array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])
numpy.matrix

广播运算

# 广播运算
a = np.array( [20,30,40,50] )
b = np.arange(4)
b
c = a-b
c
b**2
10*np.sin(a)
a<35

array([0, 1, 2, 3])
array([20, 29, 38, 47])
array([0, 1, 4, 9], dtype=int32)
array([ 9.12945251, -9.88031624,  7.4511316 , -2.62374854])
array([ True,  True, False, False])

矩阵乘法（元素乘、矩阵乘）

元素乘法：np.multiply(a,b)
矩阵乘法：np.dot(a,b) 或 np.matmul(a,b) 或 a.dot(b) 或直接用 a @ b !
唯独注意：*，在 np.array 中重载为元素乘法，在 np.matrix 中重载为矩阵乘法!

对于 np.array 对象

元素乘法 用 a*b 或 np.multiply(a,b)

>>> a
array([[1, 2],
       [3, 4]])
>>> a*a
array([[ 1,  4],
       [ 9, 16]])
>>> np.multiply(a,a)
array([[ 1,  4],
       [ 9, 16]])

矩阵乘法 用 np.dot(a,b) 或 np.matmul(a,b) 或 a.dot(b)或“@”

>>> np.dot(a,a)
array([[ 7, 10],
       [15, 22]])
>>> np.matmul(a,a)
array([[ 7, 10],
       [15, 22]])
>>> a.dot(a)
array([[ 7, 10],
       [15, 22]])
>>> a@a
array([[ 7, 10],
       [15, 22]])

对于 np.matrix 对象

元素乘法 用 np.multiply(a,b)

>>> A
matrix([[1, 2],
        [3, 4]])
>>> np.multiply(A,A)
matrix([[ 1,  4],
        [ 9, 16]])

矩阵乘法 用 “*”或“@” 或 np.dot(a,b) 或 np.matmul(a,b) 或 a.dot(b)

>>> A*A
matrix([[ 7, 10],
        [15, 22]])
>>> A@A
matrix([[ 7, 10],
        [15, 22]])
>>> np.dot(A,A)
matrix([[ 7, 10],
        [15, 22]])
>>> np.matmul(A,A)
matrix([[ 7, 10],
        [15, 22]])
>>> A.dot(A)
matrix([[ 7, 10],
        [15, 22]])

矩阵的其他操作（转置、求逆…）

import numpy as np
a = np.array([[1.0, 2.0], [3.0, 4.0]])
print(a)
a.transpose() # 转置
np.linalg.inv(a) # 求逆
u = np.eye(2) # 2x2 unit matrix; "eye" represents "I"
u
j = np.array([[0.0, -1.0], [1.0, 0.0]])
j
j @ j        # matrix product
np.trace(u)  # trace
y = np.array([[5.], [7.]])
np.linalg.solve(a, y)
np.linalg.eig(j)

[[1. 2.]
 [3. 4.]]
array([[1., 3.],
       [2., 4.]])
array([[-2. ,  1. ],
       [ 1.5, -0.5]])
array([[1., 0.],
       [0., 1.]])
array([[ 0., -1.],
       [ 1.,  0.]])
array([[-1.,  0.],
       [ 0., -1.]])
2.0
array([[-3.],
       [ 4.]])
(array([0.+1.j, 0.-1.j]),
 array([[0.70710678+0.j        , 0.70710678-0.j        ],
        [0.        -0.70710678j, 0.        +0.70710678j]]))