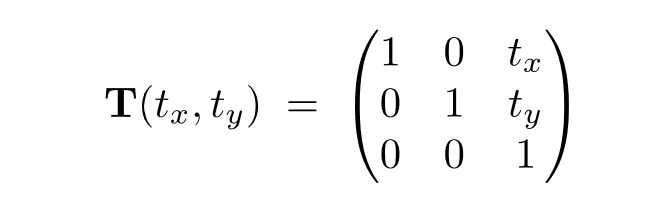变换的作用主要是模型的变化以及摄像头成像
1.2D变换：
1.1齐次坐标概念：
齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示，是指一个用于投影几何里的坐标系统，如同用于欧氏几何里的笛卡儿坐标一般。<br />**举例：**<br />当要平移一个坐标，写作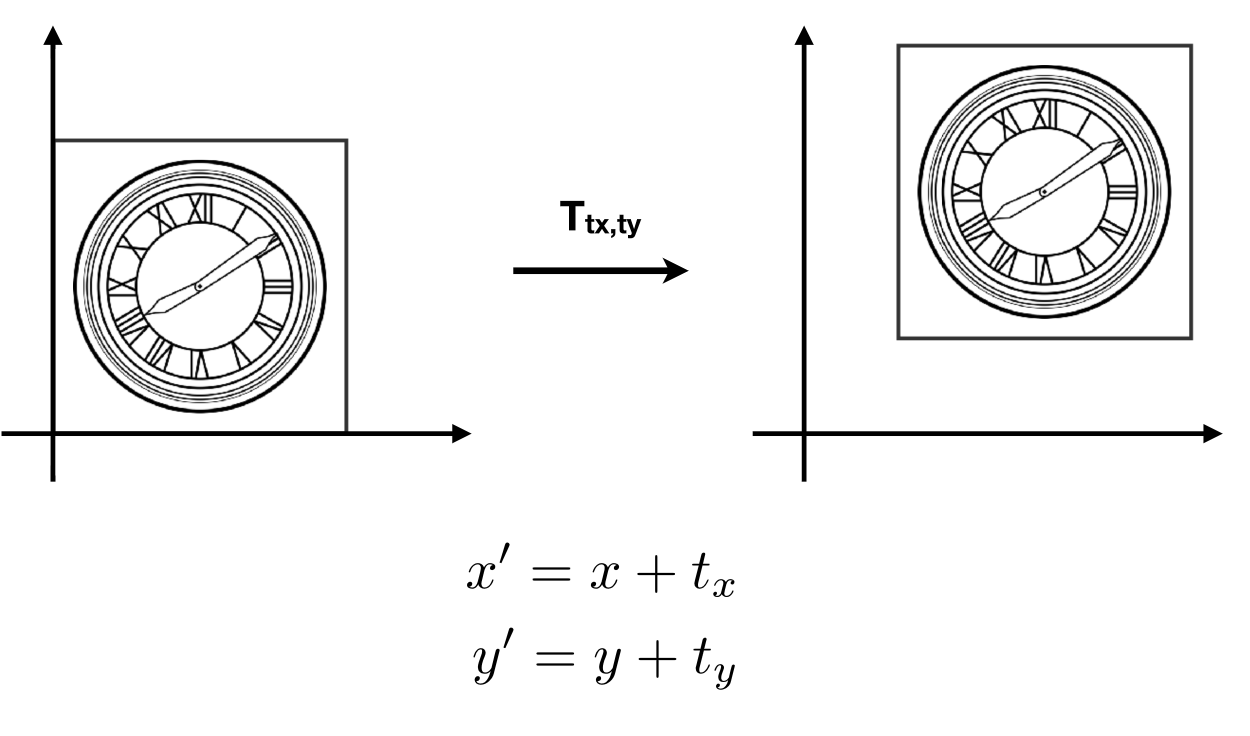：<br />如果要把方程写作矩阵：<br />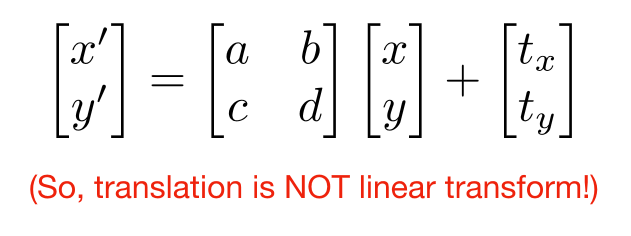<br />这里的就不属于线性变换，需要tx、ty加入到矩阵中，写作：<br />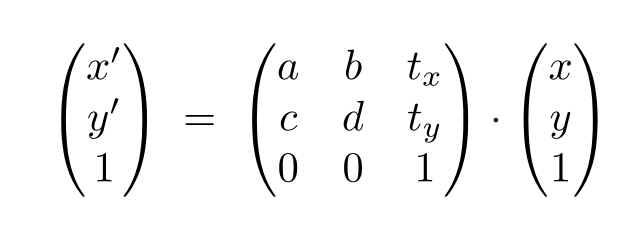<br />这里为x、y新增了一个坐标1，向量x、y则新增一个0，1代表坐标，0代表向量（向量平移，向量本身不变）：<br />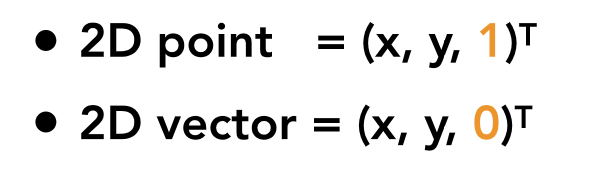<br />这里有思考问题，点+点 = 中点，因为要将W归为1，所以要x、y要除以w：<br />
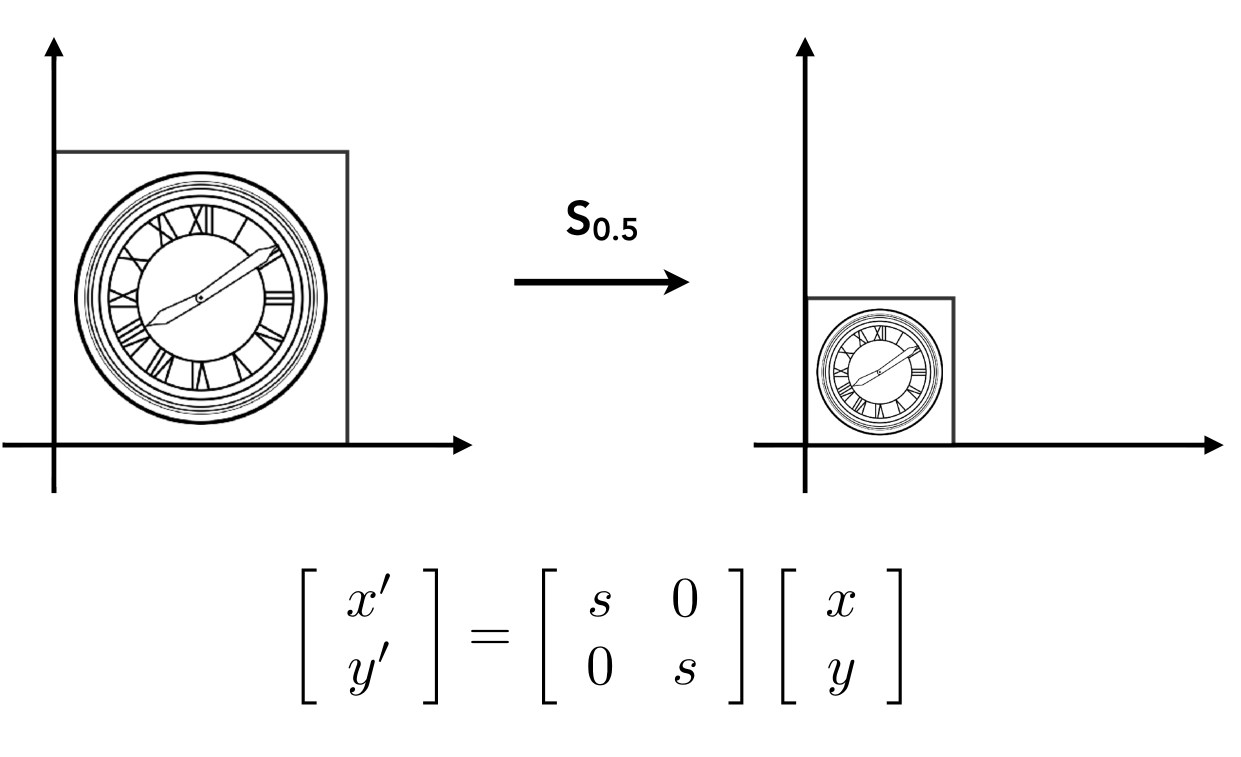
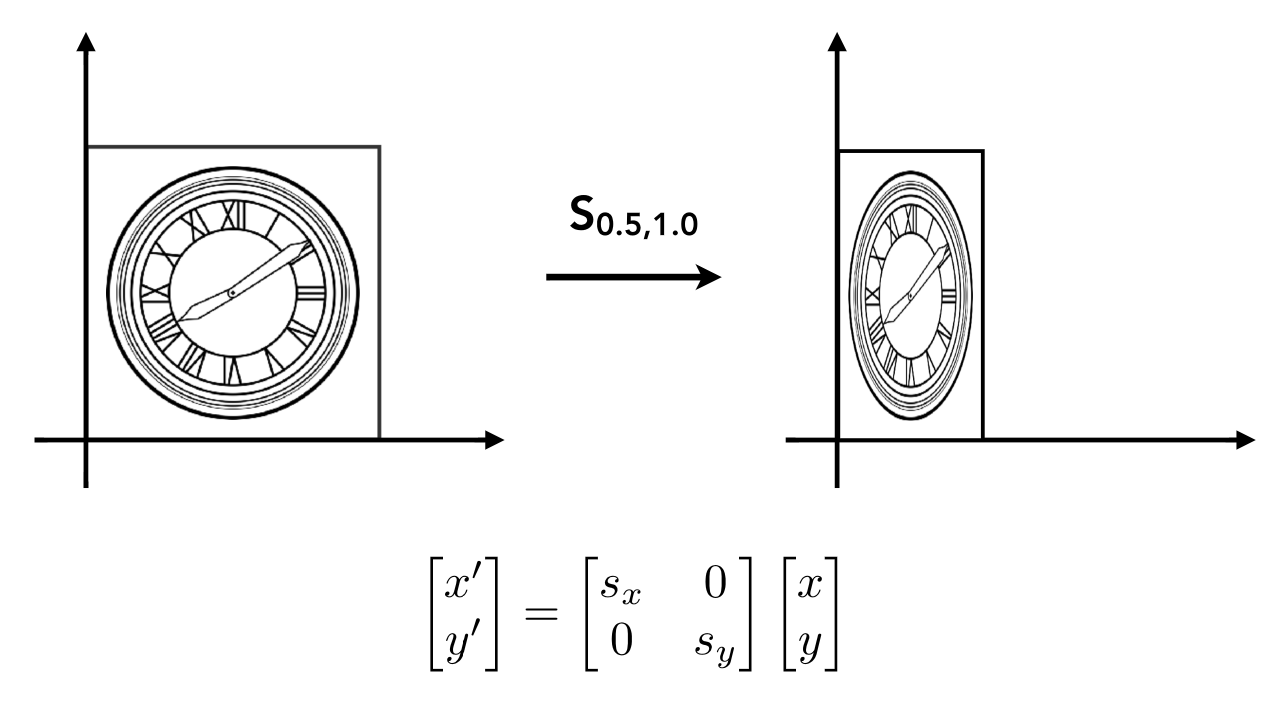
1.2 缩放变换：
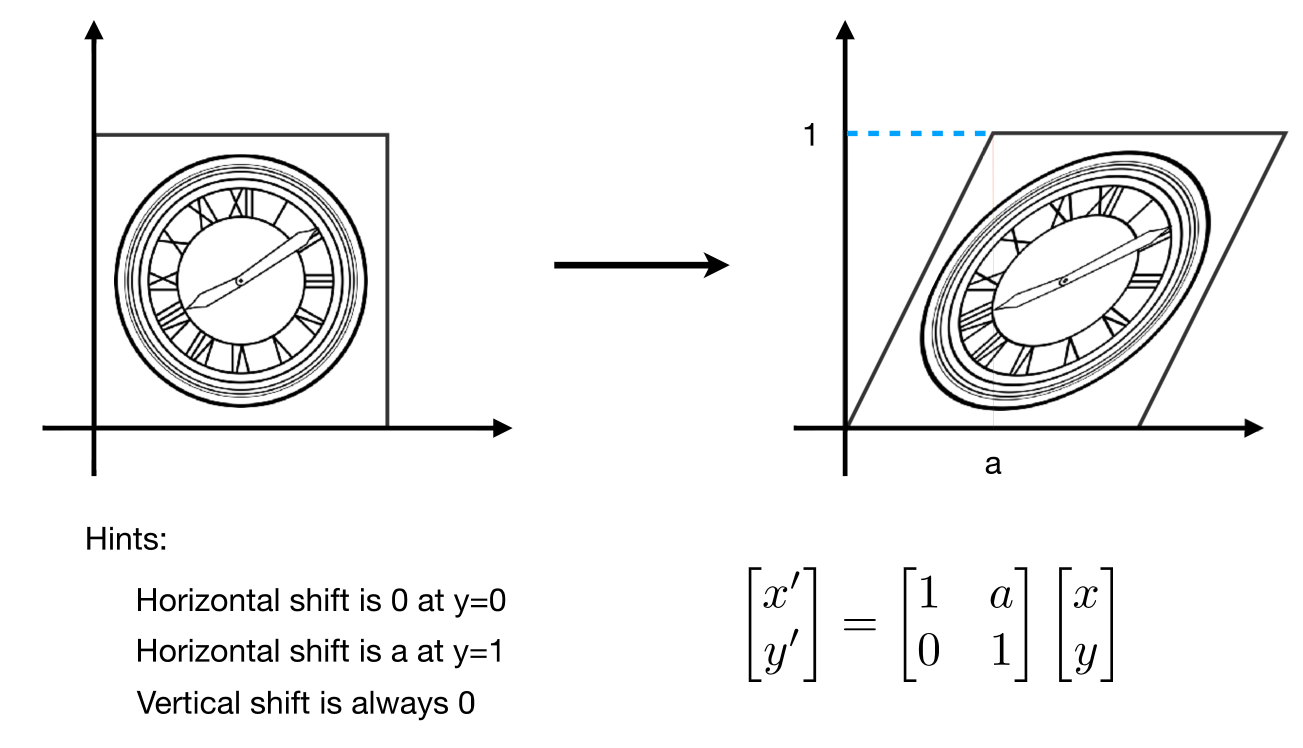
1.3 旋转变换：
假设正方形边长为1，可以根据旋转边长不变，根据夹角θ求出对边sinθ、斜边cosθ长度，从而得出向量位移信息，进一步得出变换矩阵。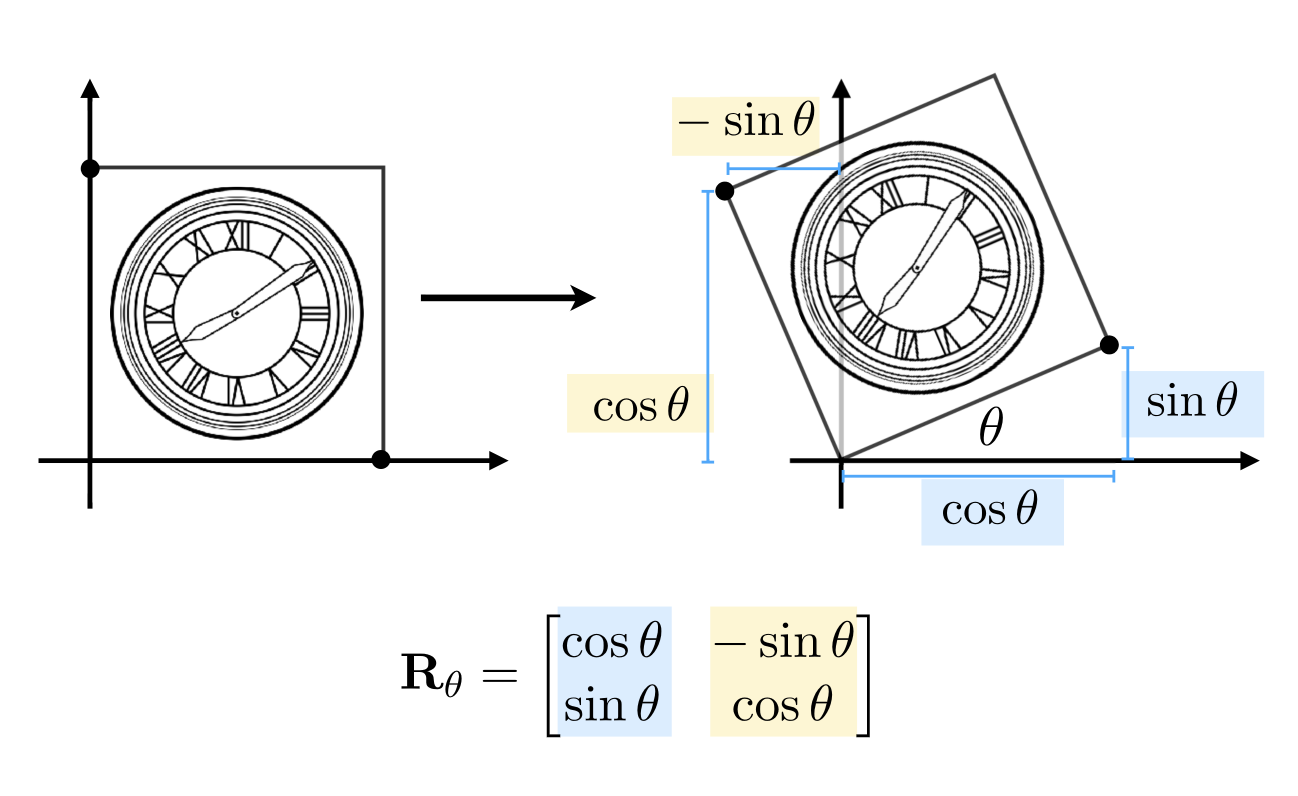
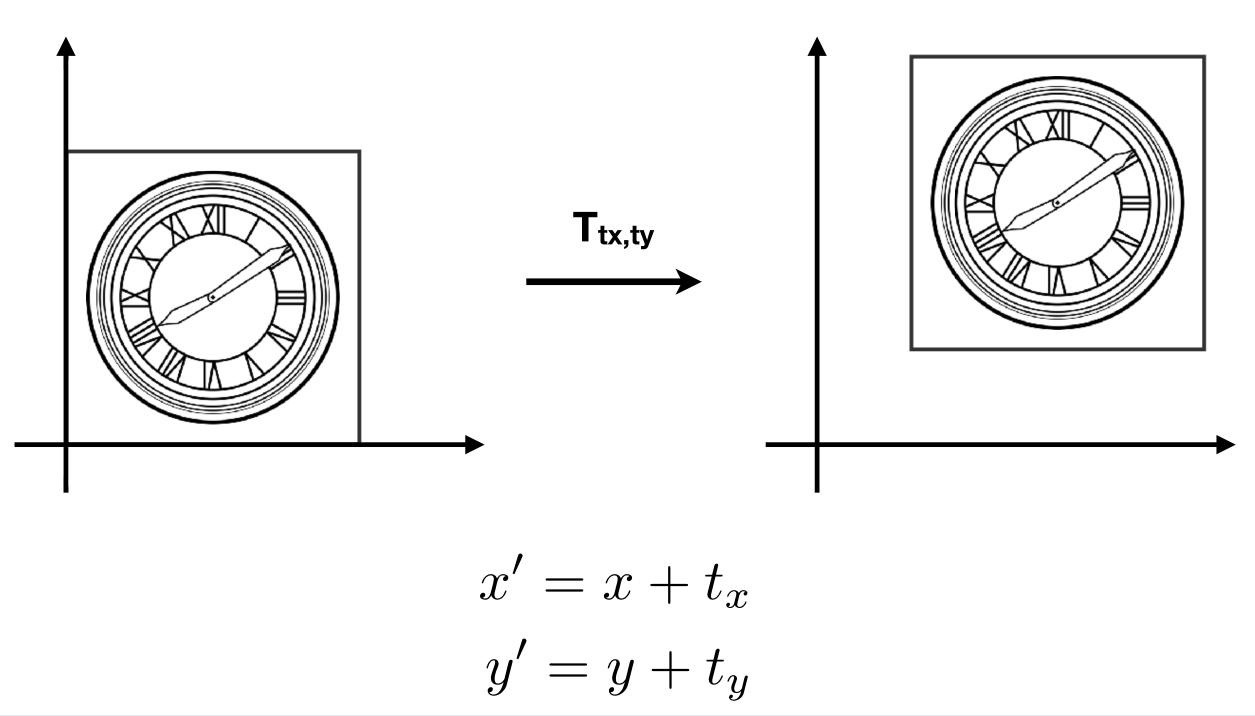
1.4平移变换：
1.5变换矩阵总结：
2.3D变换：
3D变换与2D变换相似，多一个Z方向坐标，引入齐次坐标写做：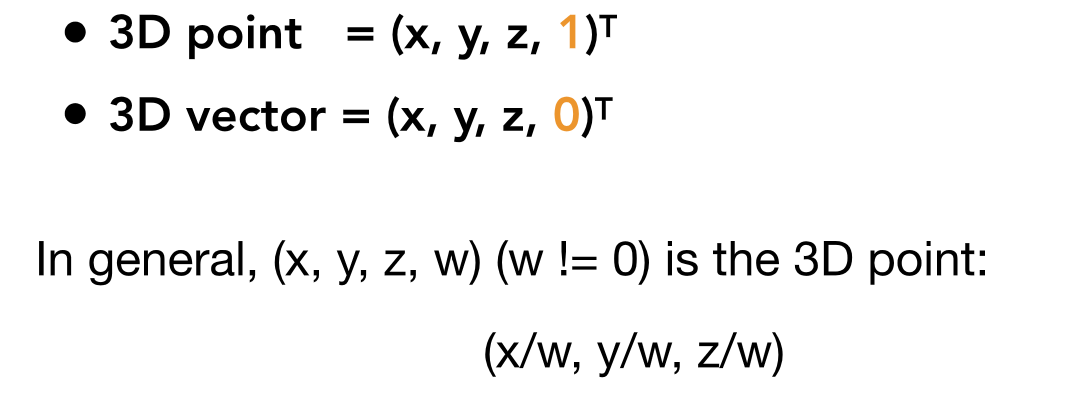
齐次坐标中，(x,y,z,1)是一个点，那么，当k!=0 , z!=0时，
(kx,ky,kz,k) 和 (xz,yz,z^2,z) 在齐次坐标中，3者都是表示同一个点
(1,0,0,1) = (2,0,0,2) =>(1,0,0)
若有收获，就点个赞吧
0 人点赞
