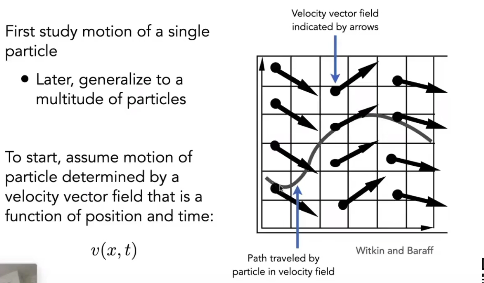
粒子运动

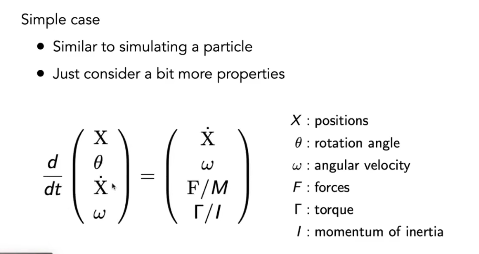
Single Particle Simulation

一个粒子在一个速度场中的速度在任何时刻是多少。
image.png

一阶常微分方程 ODE

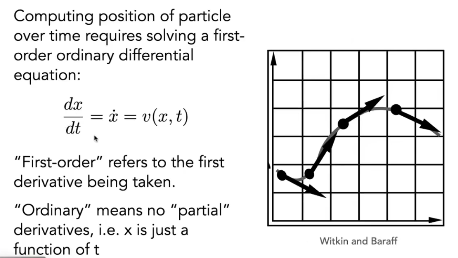
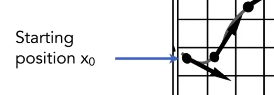
image.pngimage.png
常微分方程：一个未知函数及其导数或微分的关系式， 如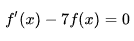： image.png。
这个“常”（Ordinary）表示平常，也就是在一般情况（理想情况）下的微分方程，即只有一个未知函数；正是因为如此，所以我们在尚未进行特殊说明的情况下，默认D.E.表示常微分方程。

显式欧拉方法解 Explicit Euler’s Method

image.png
下一帧 = 上一帧+变化量
可以看到等式左边全是下一帧，等式右边全是上一帧
他的问题就是非常不准，还会迅速不稳定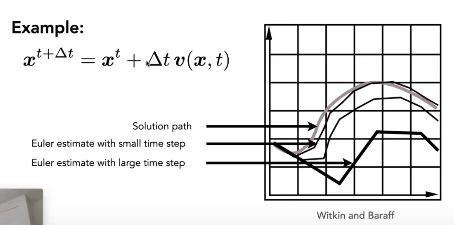
image.png 这是误差，可以通过减小Δt来优化
image.png稳定性不好，在某些情况，不管Δt多小，肯定都不会沿着该有的方法走。
这就是正反馈，出现了问题后，会把问题放大

这是用数值方法解微分方程都会遇到的问题

  • 误差
  • 不稳定

image.png

对抗不稳定性Combating Instability

中点法 Midpoint Method

修正欧拉法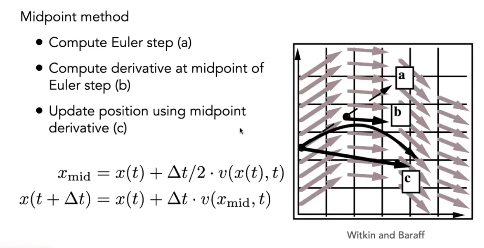
image.png
先求中点的位置，再用中点的速度计算下一帧的位置
image.png
为什么中点法更准，因为这里模拟出来了一个二次项，类似抛物线
原本的欧拉方法可以认为是线性的，修正后的是局部的二次模型，比一次好

动态步长法 Adaptive Step Size

自适应的思路，还是用中点法的思想，但是让它跟具曲线的变化率来决定每一步的步长Δt
其实就是比较上图中的a和b，如果两个相差较远那就应该把deltaT拆分的更短一点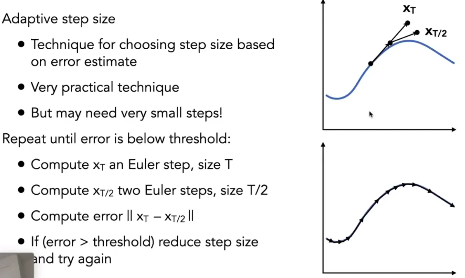
image.png

隐式欧拉方法Implicit Euler

image.png
这个跟显示的不同就是用的是下一帧的速度和加速度来计算下一帧的位置和速度
这样就不好解
拥有很好的稳定性。

如何量化稳定性 stability

用阶数表示稳定性，阶数越高越好
image.png

Runge-Kutta Families

一系列用来解ODE的方法，尤其是对于非线性的问题（非线性比线性方程在仿真的时候更好）
其中有一个RK4方法用的最广泛 （4阶）
image.png

Position-Based/Verlet Integration

不是基于物理的方法
image.png

刚体模拟Rigid body Simulation

刚体运动其实就是粒子运动，只是多考虑几个变量
image.png

流体模拟 Fluid Simulation

用流体模拟仿真来说明Position-Based/Verlet Integration 的方法
image.png
关键idea

  • 得到所有小球位置就得到了所有水的位置（渲染问题不考虑）
  • 水不可压缩，所以只要某个局部的小球密度改变了，就把他修正回来
  • 了解全局的密度状态（就是gradient descent 过程）

物理模拟中基本思路-拉格朗日法，欧拉法

Eulerian vs Lagrangian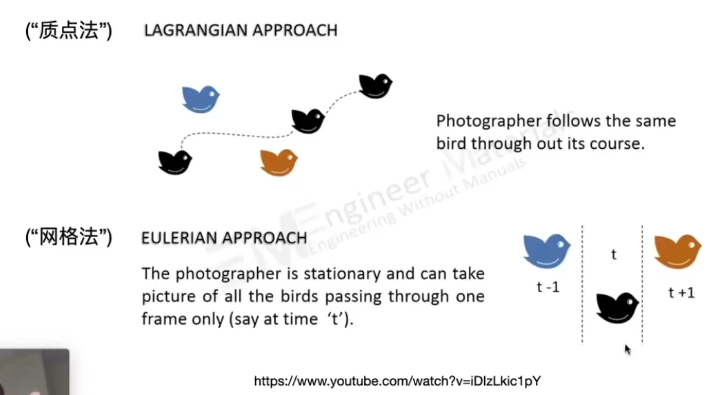
image.png
一个盯着物体看 Lagrangian 质点法
一个盯着区域格子看 Eulerian 欧拉法

一种混合的方法 MPM

image.png
把粒子转化为格子，在格子里模拟仿真，然后把结果写回到粒子里，