内容
多边形网格处理

- subdivision 细分
- simplification 简化
- regularization 正则化
细分 subdivision
细分并不只是把三角形数量提升,而是让它们的位置也随之发生一点细微的变化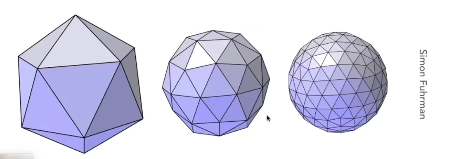
Loop subdivision
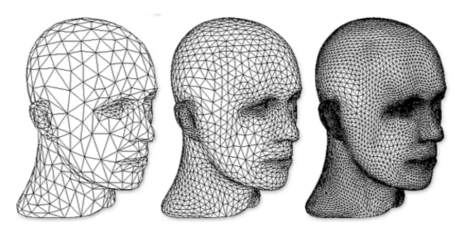
并不是循环,而是发明这个算法的人叫做loop
第一步:细分生成新的顶点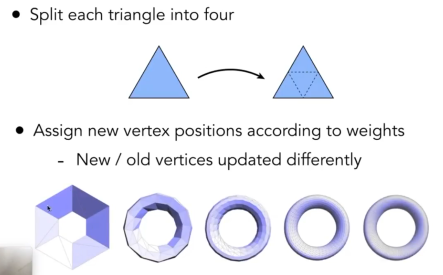
区分旧的顶点和新细分出来的顶点。
第二步,调整顶点的位置,让模型更光滑
对于新生成的顶点: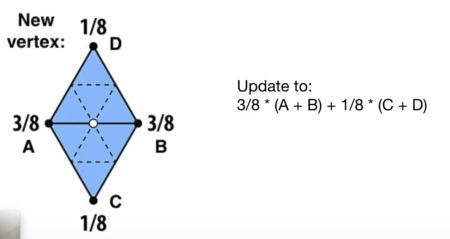
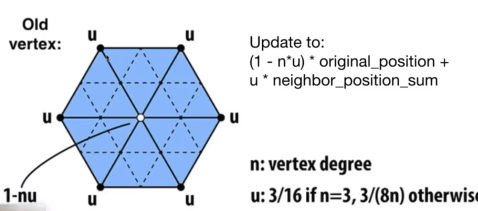
对于旧的顶点:
位置是顶点原本的位置和周围顶点位置的加权平均和。
这个权用n和u来进行计算,跟顶点的度有关。
- 度越大,周围顶点的贡献值越大
Catmull-Clark 细分
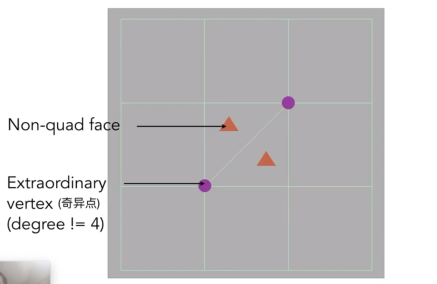
Loop细分是在三角形网格面上进行的,对于一般情况,有不同多边形的网格,是Catmull-clark细分解决的内容
quad
Extraordinary vertex 奇异点,度!=4 的顶点
第一步,细分生成新的顶点
每个面取一个中点,并且连向其边的中点。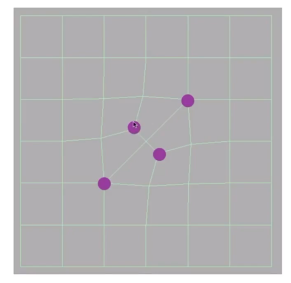
经过一次细分
- 原先的奇异点还是奇异点
- 原先的非四边形面消失,
- 但是其中心点变成了奇异点(因为非四边形面不是四条边,所以中心点的度不为4)
相当于一次细分后非四边形面都变成了奇异点,再继续细分就不可能增加奇异点了。
第二步,调整顶点的位置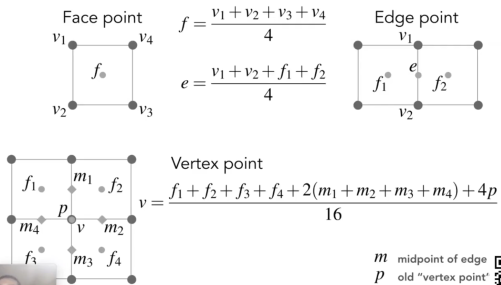
对于新的顶点:
- 定义面上的点f:周围四个点平均
- 定义边上的点e:两个端点与两个相邻面的点的平均
对于旧的顶点:
- 周围4个面点f,四个边点e和自身原来位置进行加权平均
对比loop和catmull-clark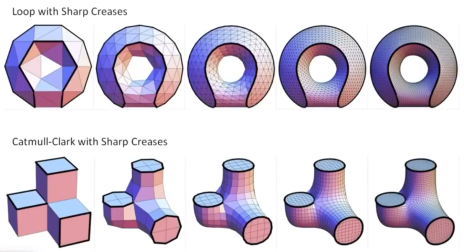
涉及到缝的问题有严格定义,这是专门的研究方向。
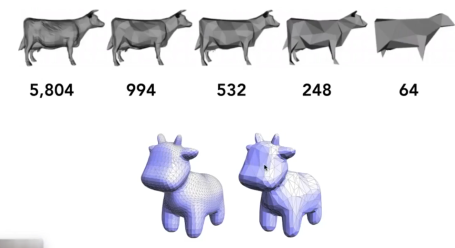
简化 simplification
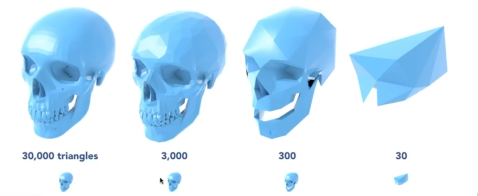
在不同情况下用不同复杂程度的模型
类似Mipmap,又是采样的问题。但是几何的层次上做没那么容易,现在有两种解决方案
- LOD level of details 细节级别
- UE5 Nanite 多边形虚拟化 详见
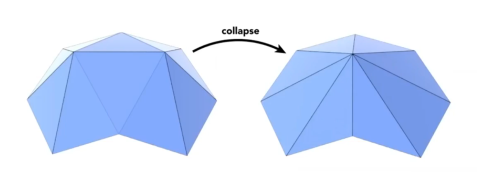
边坍缩 Edge Collapsing
二次误差度量 Quadric Error Metrics
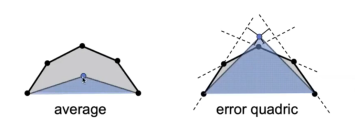
现在要去除多边形最上面三个点,新生成一个蓝色的点,求蓝色点放在什么位置,能让新生成的蓝色三角形与原来灰色多边形的大小相似
二次度量误差就是求新的点到与之相关联的点的距离的平方和 (优化过程)
坍缩一条边之后新生成的一个点,放在一个位置,有最小的二次度量误差
实现过程
- 对于每一条边,都假设对其进行坍缩,会产生多大的二次度量误差
- 保存所有边的二次度量误差成为一个序列,升序排列后,从最小二次度量误差的边开始坍缩
但是这里会出现问题,当第一条边collapse后,受影响的边位置发生变化,我们需要更新这些边的collapse值大小和序列顺序。简而言之,就是
- 求最小,
- 动态更新任何一个值
- 用优先队列这样的数据结构来做可以满足上面两点需求
- Greedy algorithm,局部最优解的和被认为是全局最优解
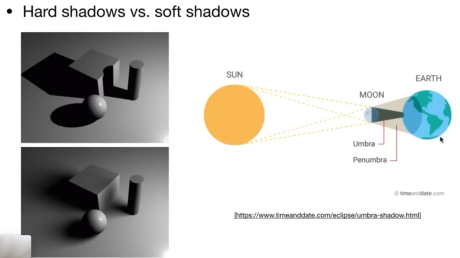
Shadow Mapping
在之前光栅化到时候,每个点着色的时候只考虑自己,不考虑其他物体也不考虑本物体的其他部分。
但是如果其他物体挡住了原本要到达这个点的光线,就会产生阴影,而不是原先的shader计算结果。
这就是阴影要单独拿出来讨论的原因
在光栅化里面做阴影,用shadow map 储存ShadowMapping技术的结果。
阴影的作用
- 强化位置感,否则就会有一种浮在空中的感觉
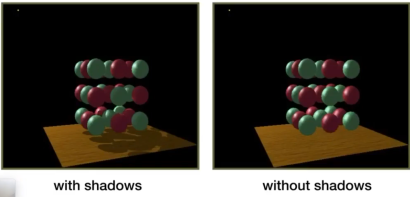
Shadow Mapping特性
- shadow mapping 是一个图像空间的算法,不需要知道场景的几何信息
- 会产生走样现象,必须要反走样
- 经典的sm只能处理点光源(硬阴影)
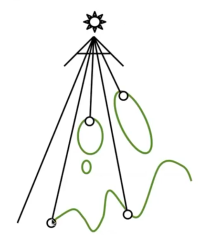
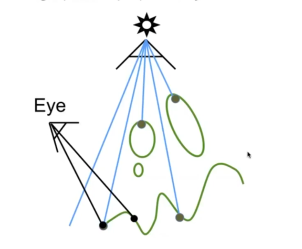
关键思想
- 如果一个点不在阴影里,那么同时满足
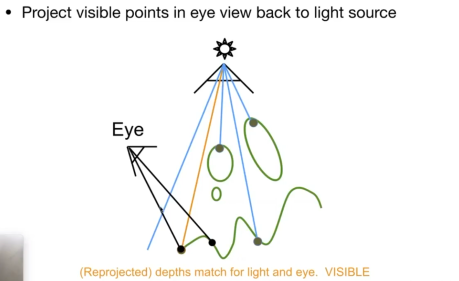
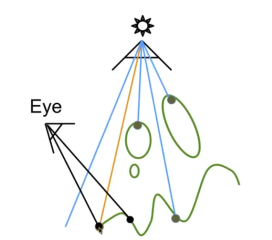
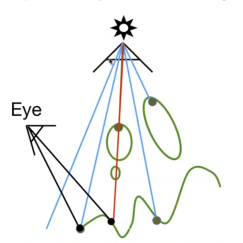
从相机看向场景,对于每一个点,
- 投影回去光源成像的图片上,找到这个点离光源的深度
- 实际计算这个点在场景中到光源的深度
如果
- 两个距离是一致的,说明这个点是可以被光源看到的
- 如果不一致,则说明这个点被遮挡了。
这样就得到了结果
这是摄像机视角的一张shadow map,里面绿色是可见;
绿色部分有杂点,这个主要是以下原因