1.向量vecto：

（数学中：向量）（物理中：矢量）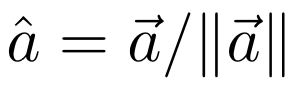

单位向量 = 向量/向量长度（模）

2.向量的点乘Dot product ：

2.1点乘的定义：

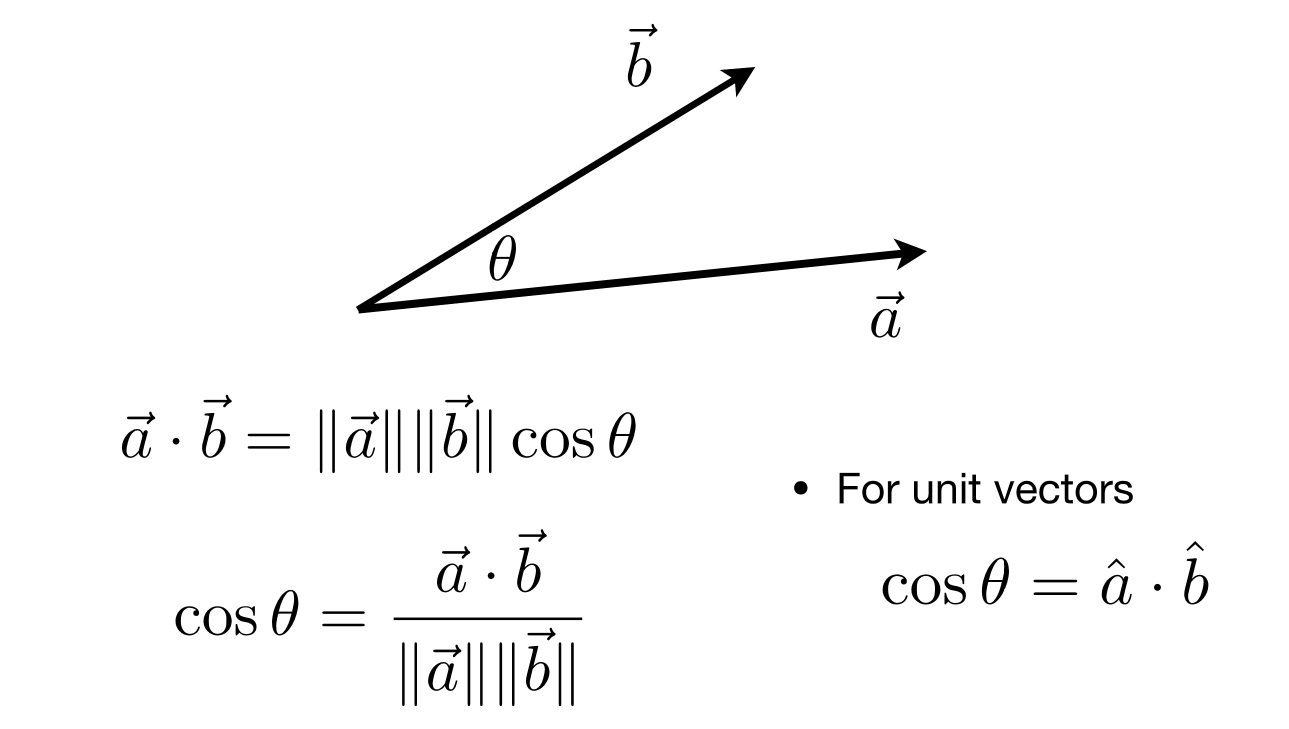
（COS是余弦(一种数学符号)。 三角形中一个角的临边(相临的短的那条边)比斜边(最长的那条边)。
COS一四象限为正，二三为正。）

2.2：点乘在笛卡尔坐标下的计算：

（笛卡尔坐标系就是直角坐标系和斜角坐标系的统称。 相交于原点的两条数轴，构成了平面仿射坐标系。）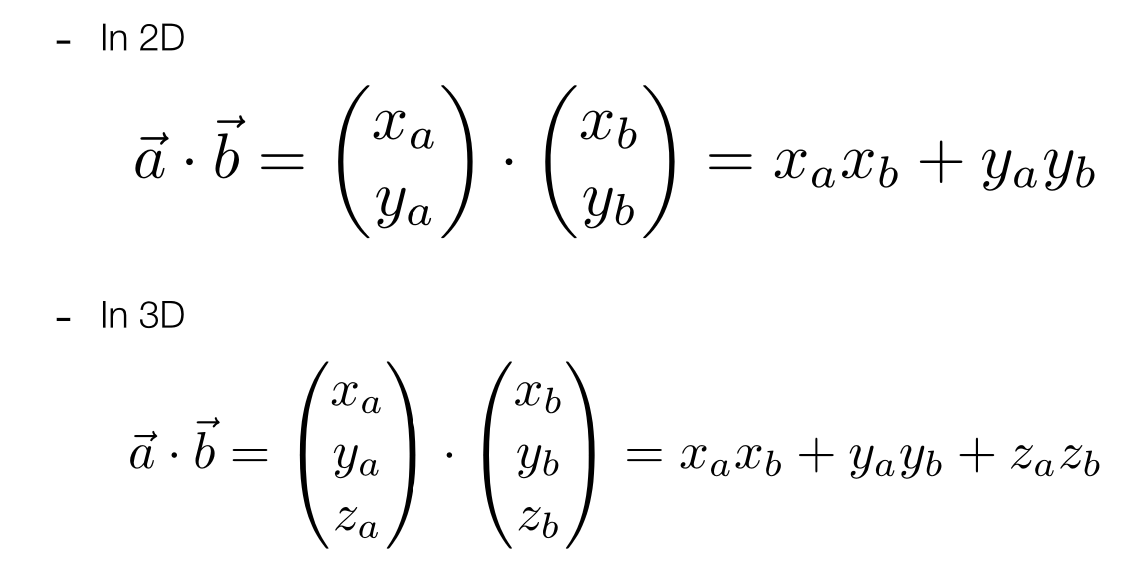

2.3向量点乘满足满足交换律、结合律、分配律：

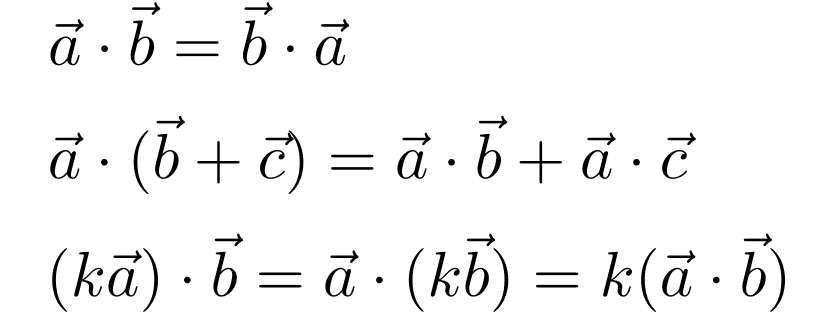
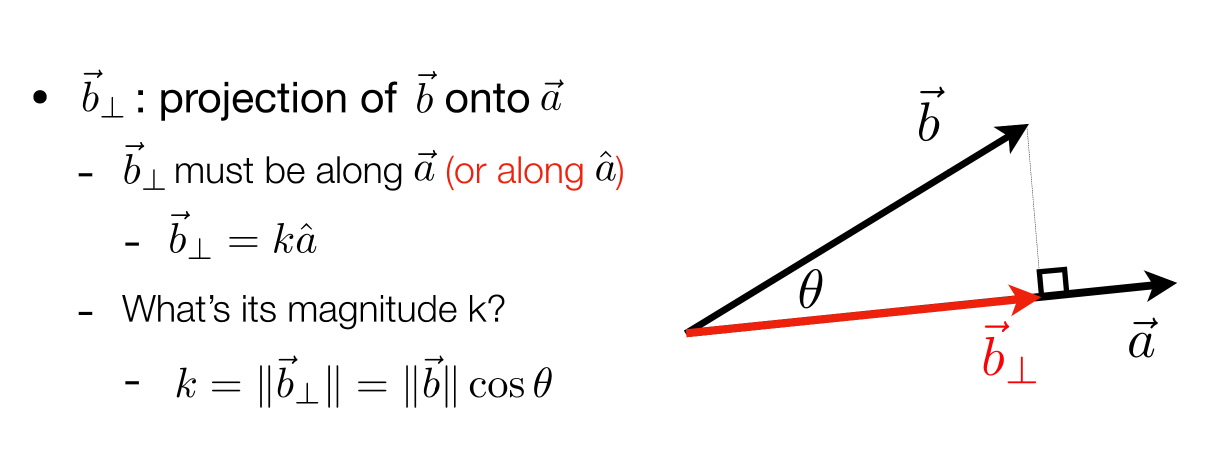
2.4点乘的作用：

1.找到向量夹角

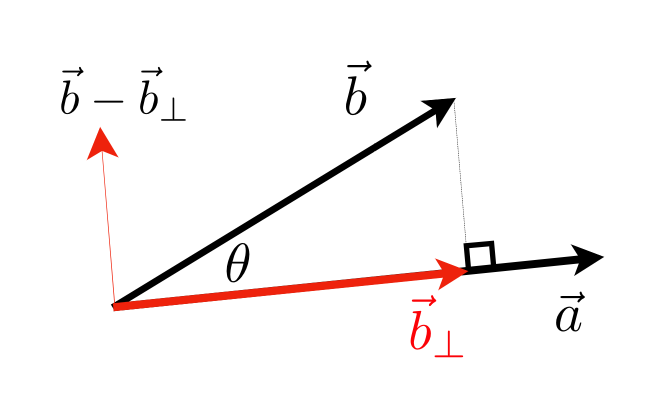
2.可以计算两个向量其中一个投影到另一个上面的长度

b投影长度= 向量b的长度*Cos夹角

3.通过一个方向的投影长度，那么就可以知道正交的另一个方向的投影长度

4.如图所示，规定虚线为界，上半部分为前，下半部分为后，（也可以理解为这是一个俯视图，原点是人物头顶，现在要判断两个向量是在人物的前方还是后方）

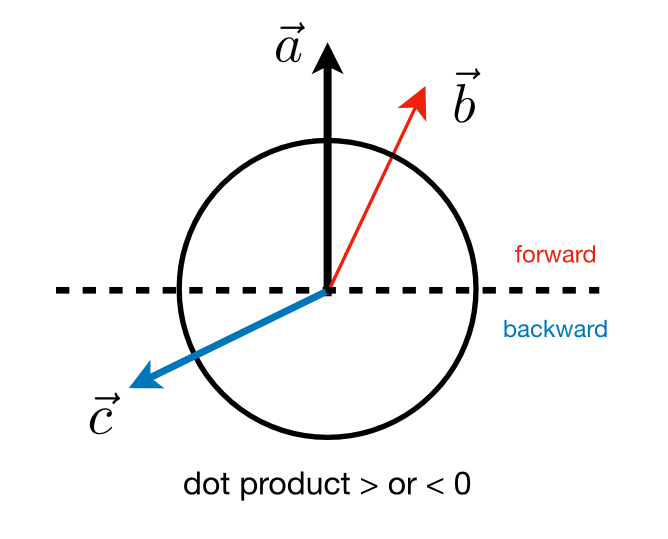
这时候只需要用a分别与b和c做点乘，结果>0,表示在前方，<0表示在后方。

5.计算两个向量接近程度

还是上面那张图，当abc都是单位向量的时候，
点乘得到的结果如果接近1，则表示两个向量很接近。（cos0°=1）
当b开始远离a直到垂直，点击结果则为0。（cos90°=0）
当b继续原理，则结果<0；这就是cos函数的性质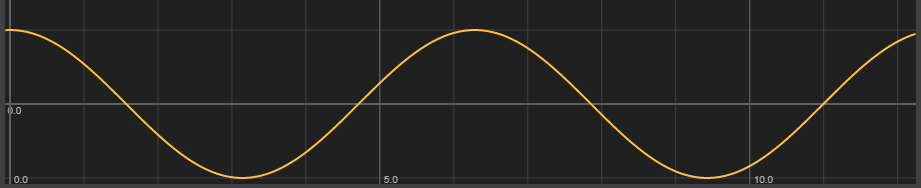

Cos的图像

3.向量的差乘Cross product：（得到新的向量）

3.1叉乘的定义：

输出向量c垂直于原本两个向量. （Sin=对边/斜边）
同时说明了，c肯定不在ab定义的平面内。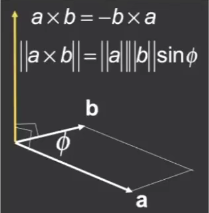

3.2右手螺旋定则：

• a叉乘b，则是右手四指从a方向往b方向握拳，此时大拇指方向则是c方向。（x×y为正=右手，为负=左手）

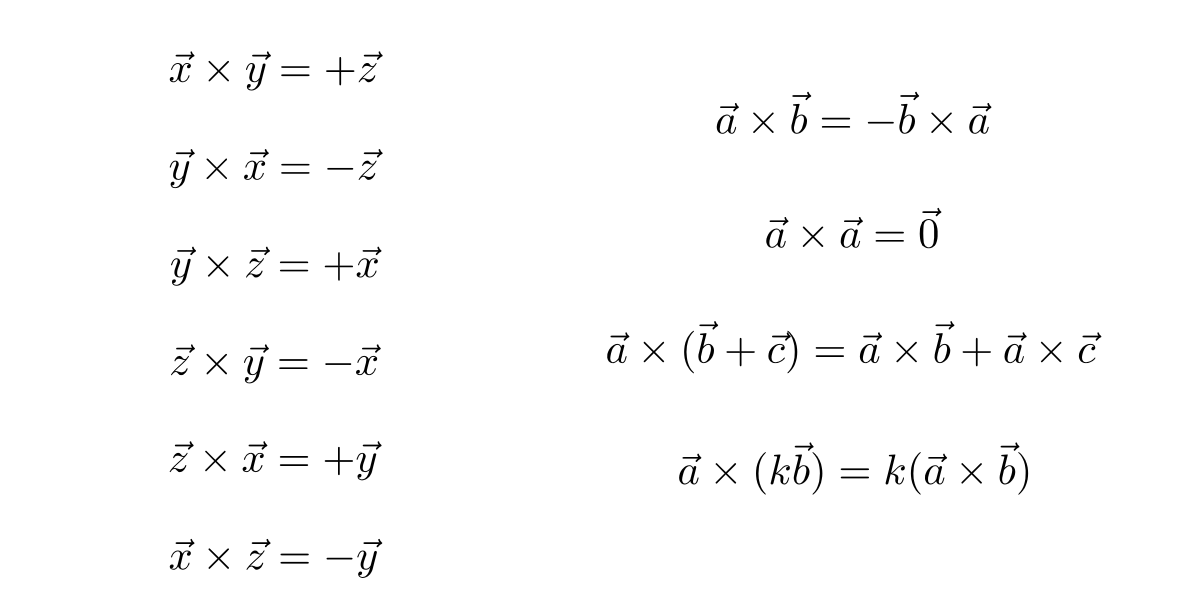
向量的叉乘不满足交换律，满足分配律、结合律。

3.3叉乘变换成矩阵形式：

3.3叉乘的作用：

3.3.1定义坐标系

因为有互相垂直关系，所以可以很方便做出自定义坐标系

3.3.2判断左/右、内部/外部

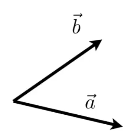可以看出来b在a的左侧，如何计算呢，很简单
axb，结果为正，则b在a的左侧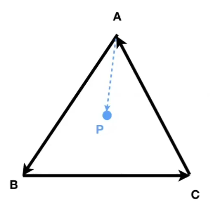
可以看出来p在三角形abc内部，但是如何计算呢
顺时针来，用ABxAP，BCxBP，CAxCP，得到结果都是正，那么p就在abc围城的三角形内部。
注意一定是这个顺序，也可以 逆时针，也可以结果为负，总之要保证乘的顺序连续。

4.矩阵Matrix：

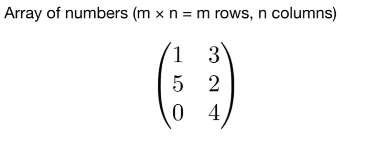
#定义一个矩阵X
X = array([[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16],[17,18,19,20]])
#X[:,0]就是取矩阵X的所有行的第0列的元素，X[:,1] 就是取所有行的第1列的元素。
# X[:,  m:n]即取矩阵X的所有行中的的第m到n-1列数据，含左不含右。
#X[0,:]就是取矩阵X的第0行的所有元素，X[1,:]取矩阵X的第一行的所有元素。

4.1矩阵的运算：

矩阵的加减：

矩阵的乘法：