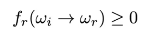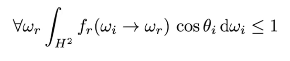材质和外观
图形学的材质是什么
Material == BRDF
因为BRDF决定了光如何与物体交互,即决定了最终采样效果
简单漫反射模型解释吸收率
之前在Bliinphong模型中设置过一个经验性模型里面有个吸收率k
这里,用一个准确的方法来定义颜色albedo,也就是能量吸收
假设物体上有一束光线Li摄入,物体不吸收任何光线全部均匀反弹,
那么就有Li = Lo ,又因为这是均匀入射光的漫反射,所以L和f都是常数,拿出来,积分半球的cos是pi
由此可以得到这个fr = 1/PI
我们把1替换成p,也就是albedo,定义为一个0-1范围上的数
所以,BRDF的取值范围是0-1/pi,因为能量守恒,所以取值不会超过1也不会为负
这就是吸收率,也就是我们的颜色。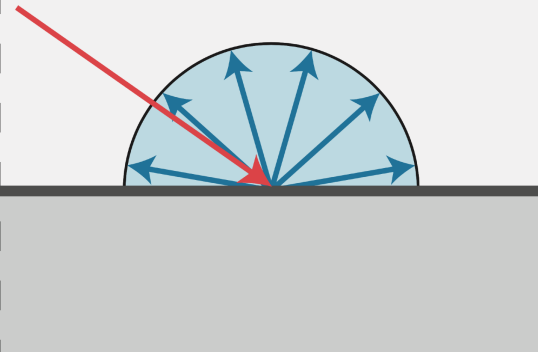
当物体吸收所有光的时候,albedo = 0 ,呈现黑色
当物体反射所有光的时候,albedo = 1 ,呈现白色
Glossy反射
介于镜面反射和漫反射之间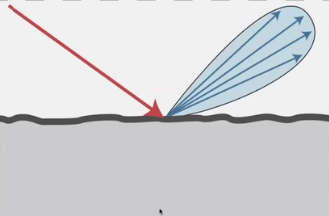

Reflective物体
玻璃或者水,表面光滑有反射有折射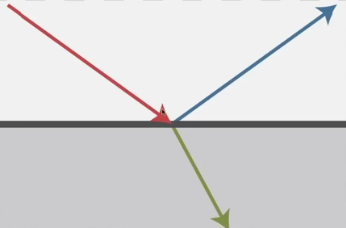

折射即BTDF,玻璃最终的效果是BRDF+BTDF,那就是BSDF
完美镜面反射 Reflection
反射定律

计算方法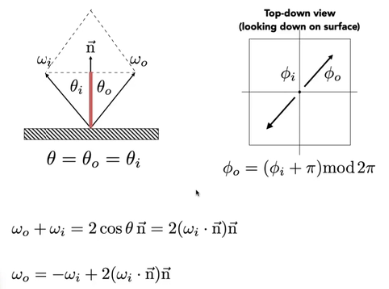
结果
镜面反射的BRDF值
这个值是多少
需要引入一个delta函数
没有过多展开说明
镜面折射 specular refraction

几何光学,光在进入镜面后,根据波长不同会造成不同角度的折射。(这就是为什么折射的光学是彩色的)
产生caustics (右下角)翻译为焦散,原因是折射的光纤线在某处聚集
Snell‘s Law 折射定律
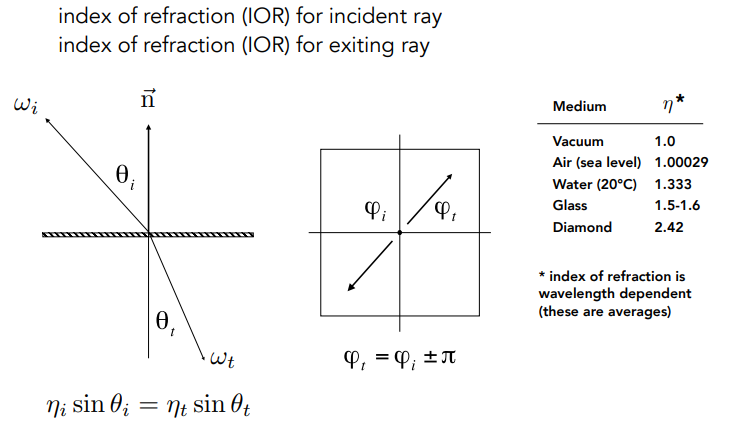
通过这个推导全反射现象: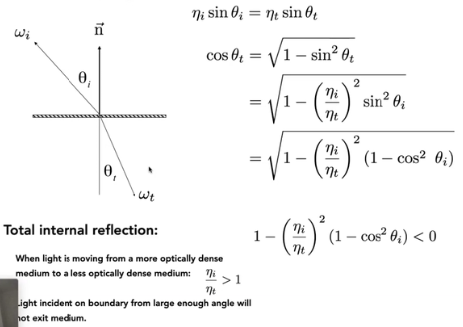
当入射介质的折射率小于折射介质的折射率的时候,就有可能出现全反射,没有折射存在。
比如说当光从空气进入水里的时候,就在一定的入射角度上没有折射(例如掠射角),全反射了。
Snell’s Window 的现象 - 部分角度内部全反射

大于97.2度的光线直接被反射走了,没有折射效果,进入不了水里,所以看不见。
Fresnel Term 菲尼尔项
Everything has fresnel
有多少光被反射折射,跟入射光角度是有关系的。例如入射角垂直,那么反射比较少,折射比较多。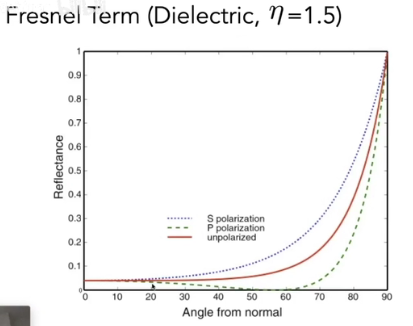
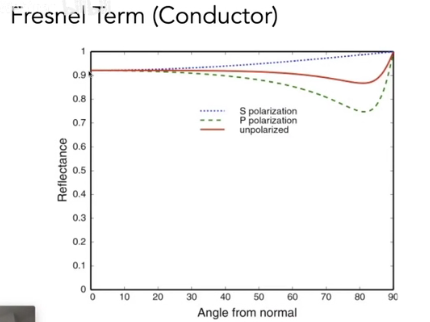
主要看红线, 另外两条是极化的情况
左图是折射率是1.5的绝缘体,不同物体是不同的。对于导体,可以看到,不管入射角度与物体表面法线多么接近,都会发射很大的反射,而不是产生很多折射
另外,导体的折射率是复数
计算Fresnel
准确的方法
计算起来比较麻烦,所以有了简化版本:Schlick’s Approximation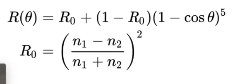
其实就是把上图两个曲线给简化了,通过测量可以发现其实相差还是挺大的。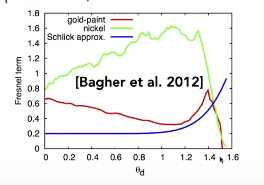
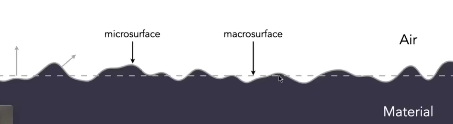
微表面材质 Microfacet Material

宇航员从太空拍摄地球,发现从远处看看不到表面那么多细节。从远处看居然是平面,可以很好的反射光
是什么 Microfacet Theory
- Macroscale:从远处看,是材质外观,flat&rough
- 从远处看就是一个平面
- Microscale:从近处看,是几何,bumpy&specular
- 每一个微表面都认为是一个微小的镜面
- 每一个微表面都有自己的normal朝向法线
微表面模型与材质表现
宏观状态 - 微观分布 - 材质效果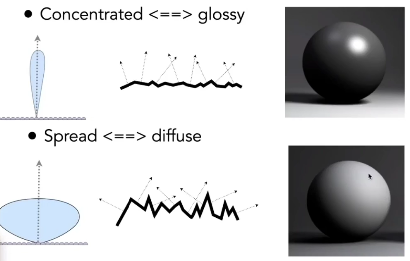
所以我们可以把表面的粗糙程度用微表面来表示,决定了
- 漫反射
- 镜面反射
- glossy
Microfacet BRDF
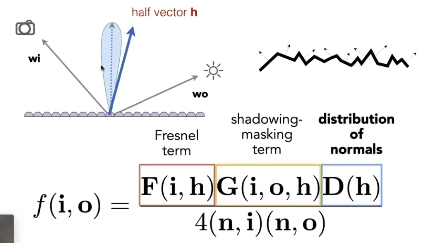
half vector h 的作用 :只有微表面的法线方向沿着h方向(因为微表面考虑的是完全镜面,完美反射)才能把光反射到出射方向去。判断什么样的微表面才能把入射方向的光反射到指定方向去
F:Fresnel Term : 总共有多少能量被反射
G :Shadowing masking Term : 几何项,微表面自己给自己阴影,互相遮挡。尤其是当光线几乎是平着打到物体表面上的时候: Grazing Angle 掠射角度
D :Distribution of normals : 决定性的,法线分布
分母 :变换和归一化
效果很好

现在的PBR基本上会用微表面模型
具体实现可能有很多不同微表面模型,但是思路是一致的
缺点在于漫反射项可能不准
各向异性 Anistropic Materials (BRDFs)


就是磨过的金属的拉丝效果
各向同性,各向异性
从微表面理解,各向同性的反射方向分布均匀,朝各个方向
各项异性的反射有统一的方向
对于BRDF来说就是: 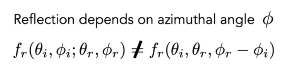
从BRDF理解,就是入射角和出射角沿着法线轴旋转得到的结果不同那就是各向异性,即各个方向结果不同。(不只跟相对方位角相关,还跟绝对方位角有关)
各向异性比较特殊的材质
尼龙
天鹅绒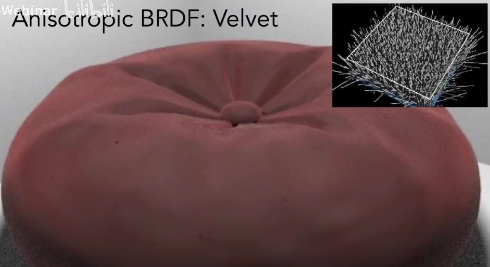

天鹅绒因为可以人为的改变微表面方向,所以是各向异性
各种BRDF的性质
1 能量非负
2 线性性质,各部分相加
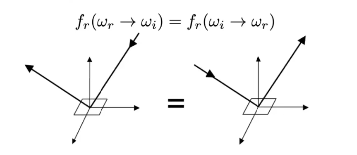
3 可逆性,交互入射方向和出射方向,得到的值一模一样
4 能量守恒
5 各向同性的BRDF变成三维的问题
三维就是三个变量
两个出射角度还有两个入射角度,本来就是四维问题
现在有一个方向无关,那就是三维的。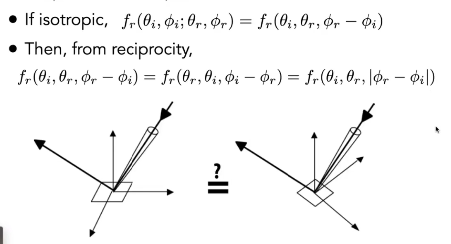
好处就是储存BRDF少了一维的空间。
测量BRDFs Measuring
物理上的模型和实现上的情况还有有很多不一样的。所以有很多时候需要去做测量。
测量的数据很多可以直接用到计算中,而不用去推导,这样又准确又快。
Image-Based BRDF Measurement
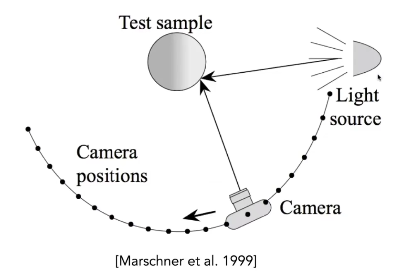
让灯和相机从四面八方去照射和拍摄,这样记录下所有可能的结果 左图的机器可以精确到0.1°
左图的机器可以精确到0.1°
计算方法
这样是4维的,我们需要优化数据,
- 对于各项同性材质,我们可以降到3维
- 利用可逆性,只考虑相对方位角。所以又可以把数据量减少一半
- 其他采样测量,比如猜测