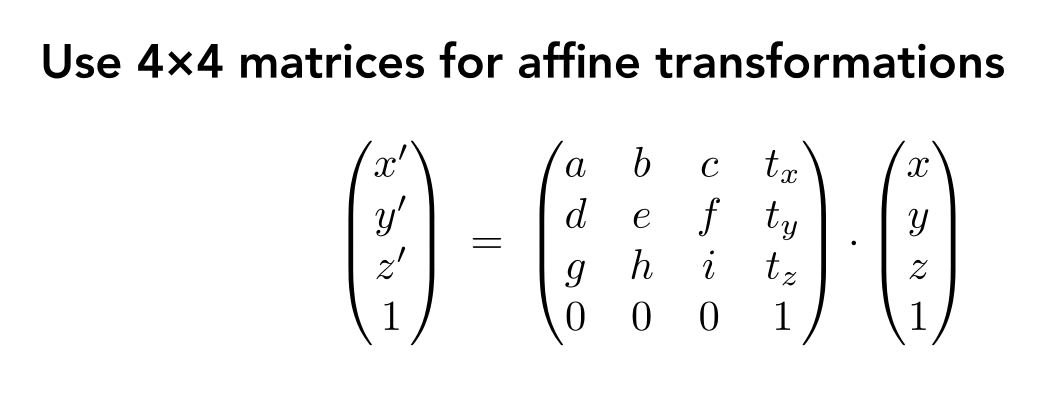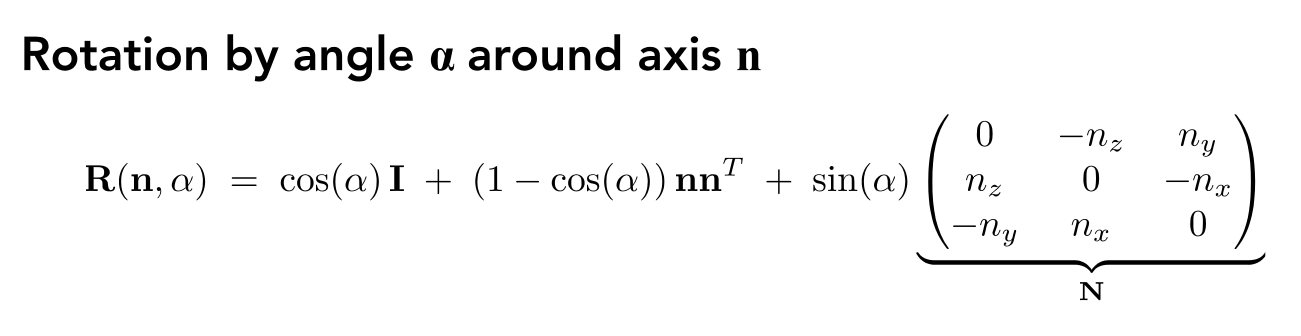矩阵定义补充：

矩阵计算从右往左。

单位矩阵：

在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1，这种矩阵被称为单位矩阵。它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0。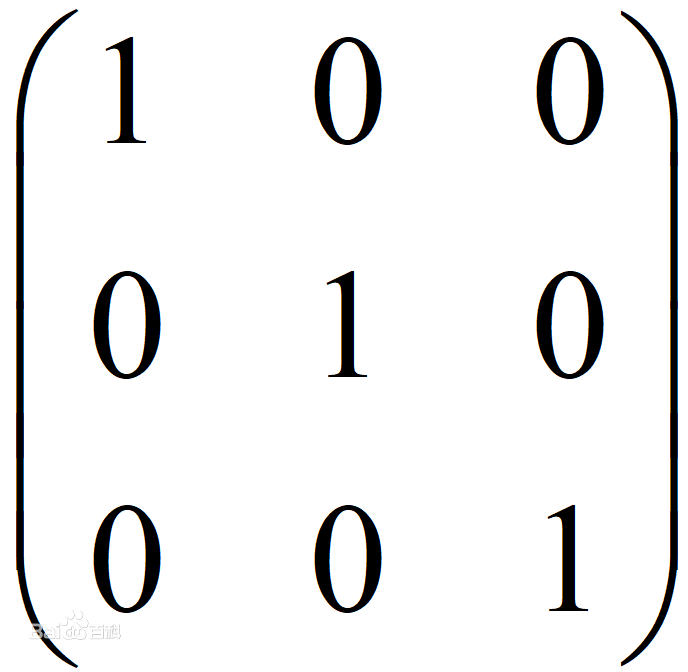

正交矩阵：

如果AAT=E（E为单位矩阵，AT表示“矩阵A的转置矩阵”）或ATA=E，则n阶实矩阵A称为正交矩阵。

矩阵转置：

行变为列，列变为行。

1.矩阵3D变换：

1.1缩放平移矩阵：

2.2旋转矩阵变换：

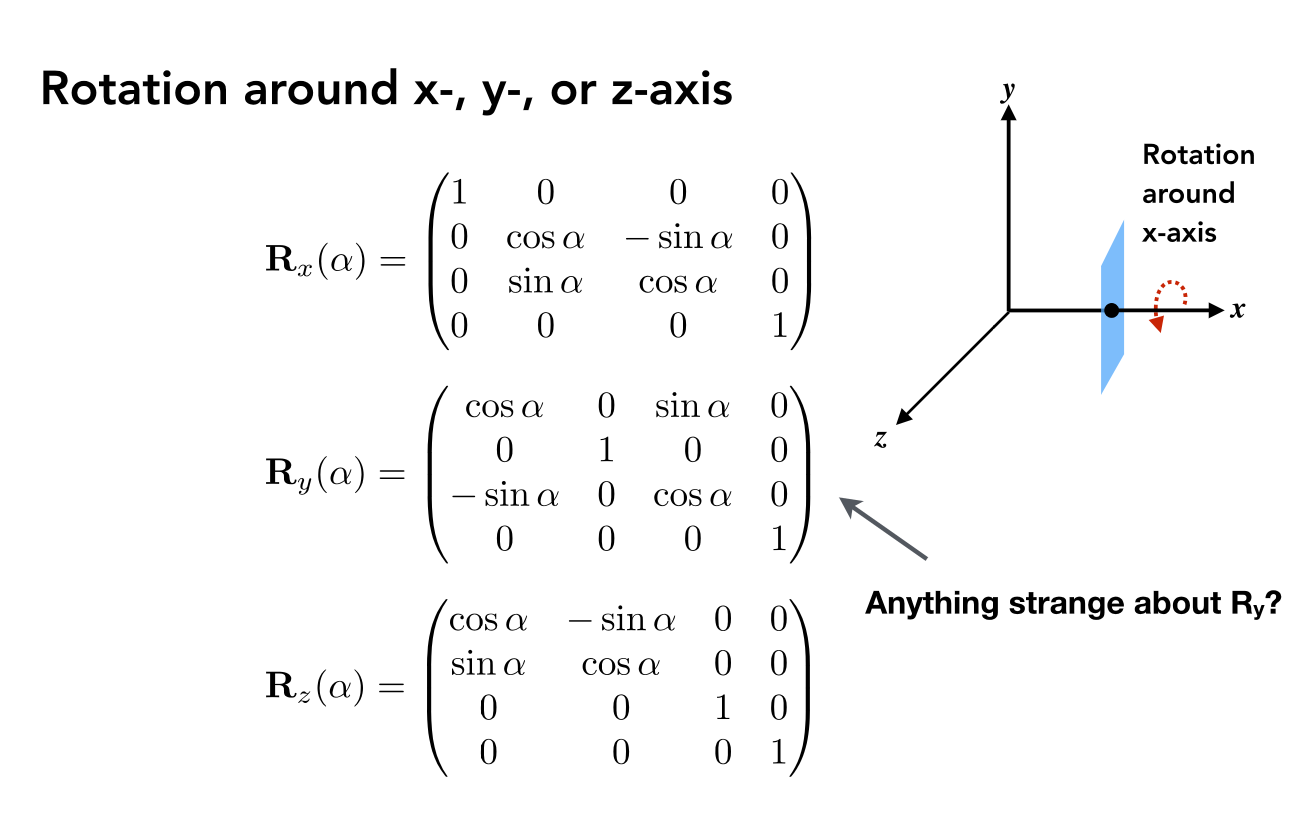
Ry 为 负的原因：
Rx为y叉乘z
Rz为x叉乘y
而Ry为z叉乘x，根据：
右手定则：XYZ按顺序叉乘，结果为正。按反序叉乘，结果为负。
左手定则：XYZ按顺序叉乘，结果为负。按反序叉乘，结果为正。

2.3在任意轴旋转变换：

可以拆分为矩阵的叉乘

2.4四元数：

旋转矩阵没法计算差值
比如说，旋转20度的矩阵和旋转40度的矩阵相加求平均并不是旋转30度的矩阵
四元数就是为了解决这个问题的。

3.Viewing transformation观测变换：

3.1观测相机：

观测顺序：1.确定相机位置（确定相机坐标系原点）
2.确定视角变换（确定摄像头朝向，即确定z轴方向）
3.确定相机抬头方向（确定摄像头旋转角度，即确定相机y轴方向）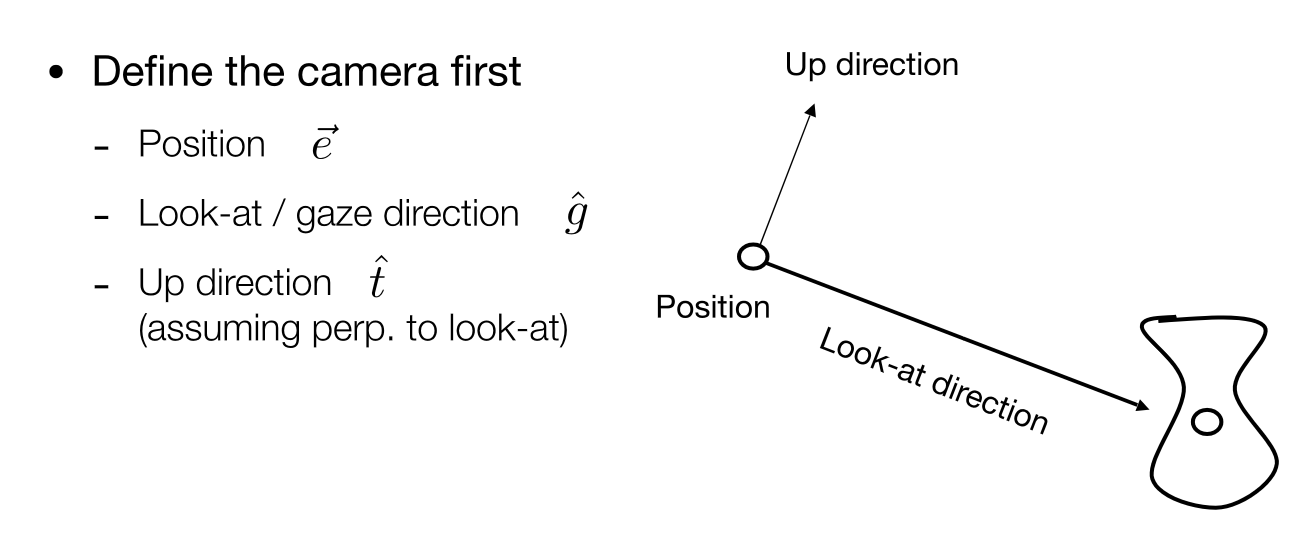

观测相机用矩阵表示：

WHY?
因为正交矩阵的逆矩阵等于它的转置矩阵。

3.2正交投影：

正交投影可以理解为将相机拉到无限远，没有近大远小变换。
在空间中亦可以理解为去掉图像点的z轴信息：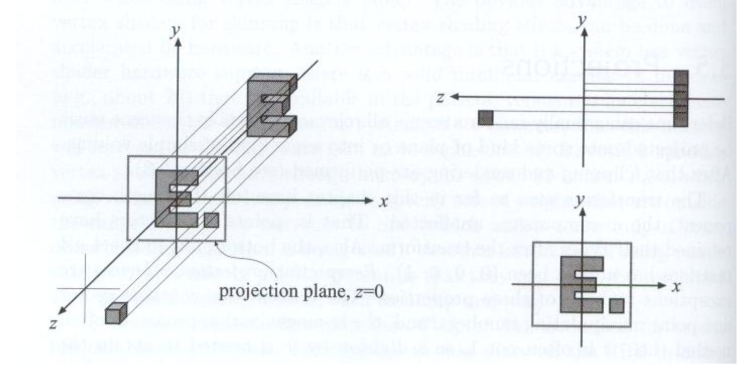

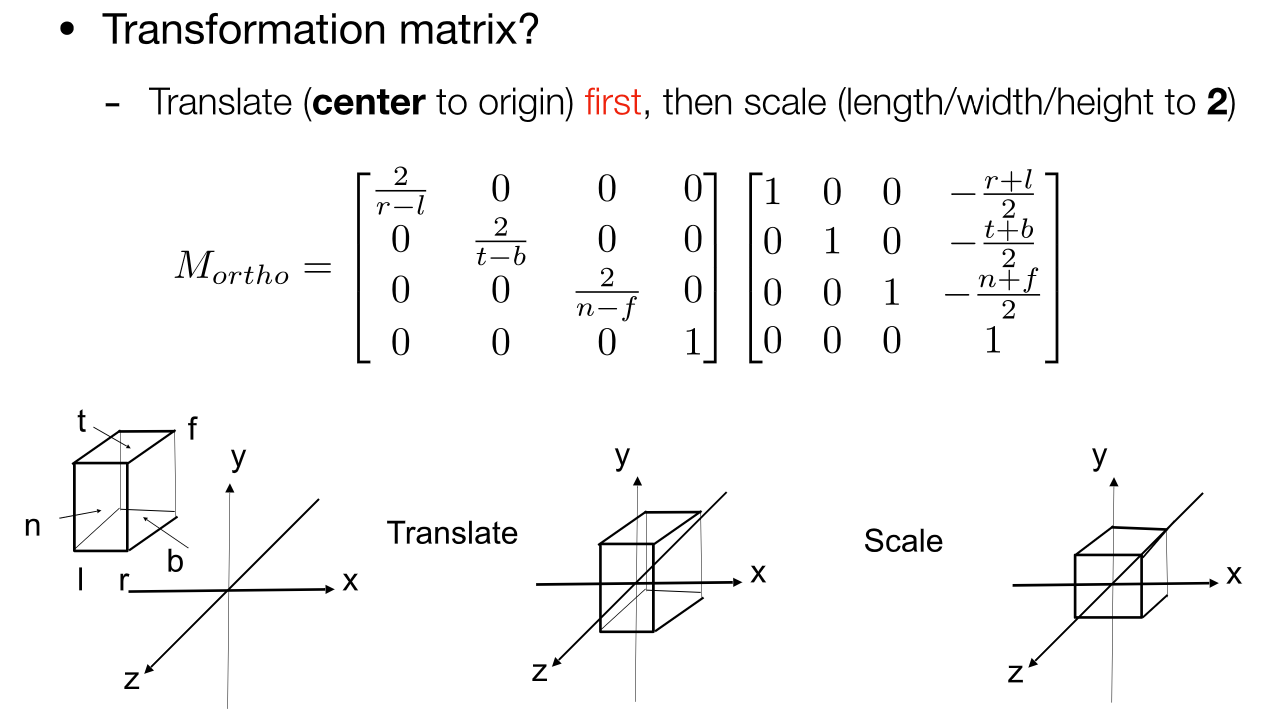
正式的做法：
把一个cuboid [l,r] x [b,t] x [f,n] (左右，下上，远近)映射到一个 canonical（正则、规范、标准） cube [-1,1]3

顺序先平移再缩放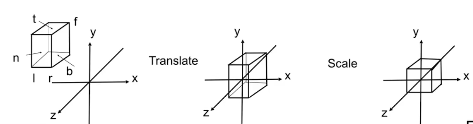

这里重点看远近平面，因为我们是右手系，从-Z看，所以物体越远，值越小，越近，值越大（归一化前）
所以远值<近值

写作矩阵：

3.3透视投影：

透视投影可以理解为先把远平面压缩为显示平面大小，然后进行正交投影。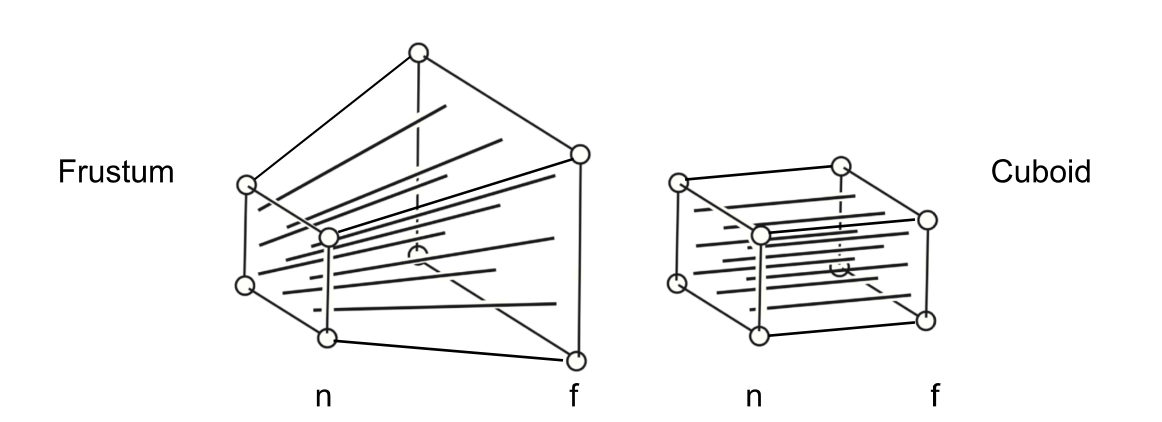

坐标压缩方法：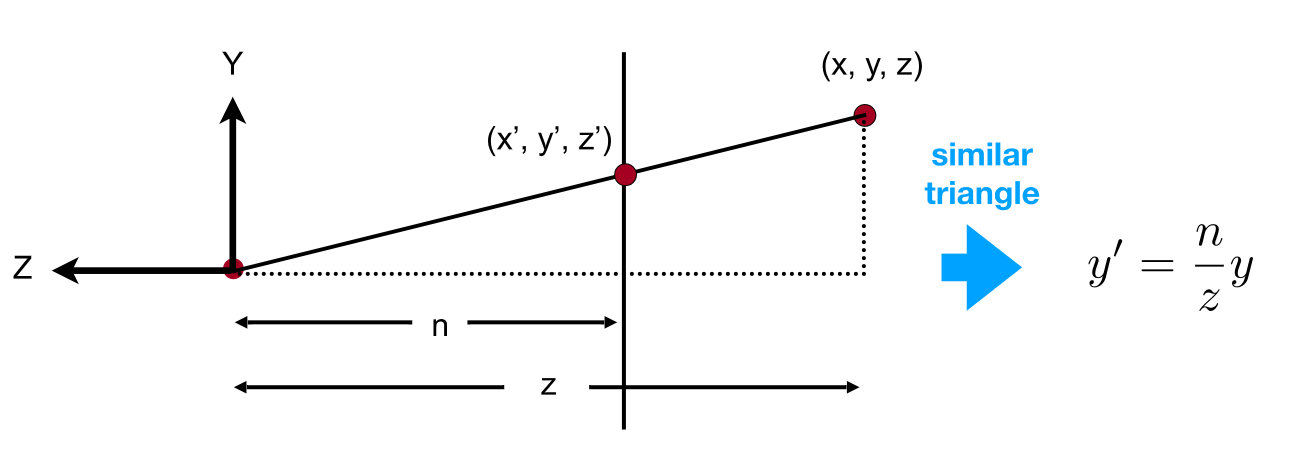

压缩后的坐标为：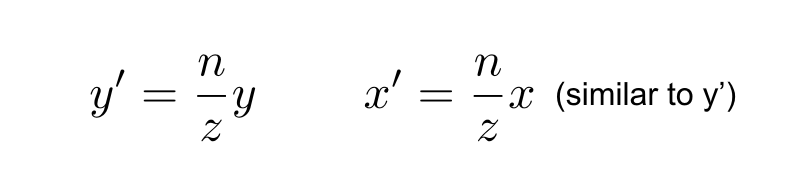

压缩后的坐标写成矩阵，然后同乘z（齐次坐标定义）：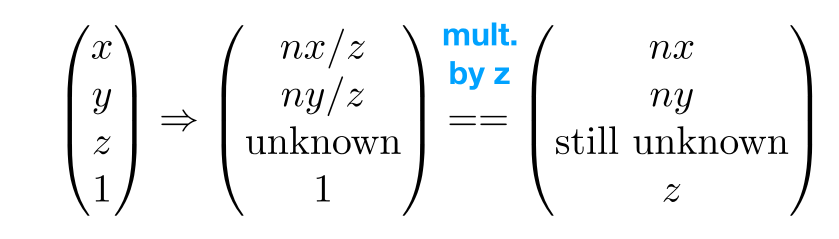

最后得到：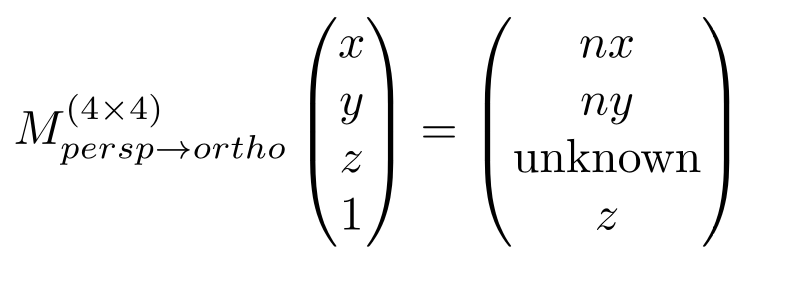

在远平面压缩中，中心点以及z的位置是不变的，可以以此解决unknow的值：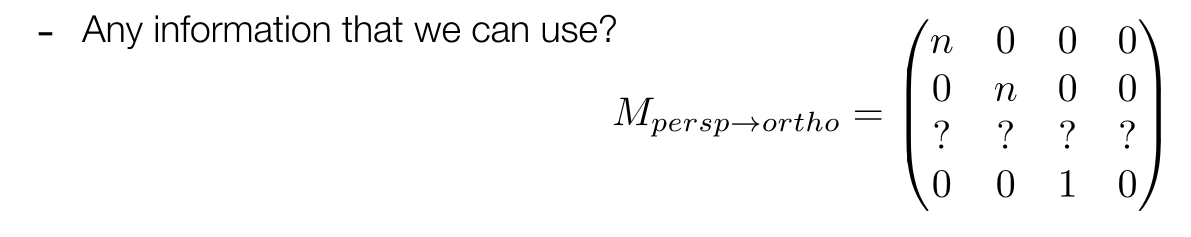

z值不变，所以把z值替换为n，再乘n：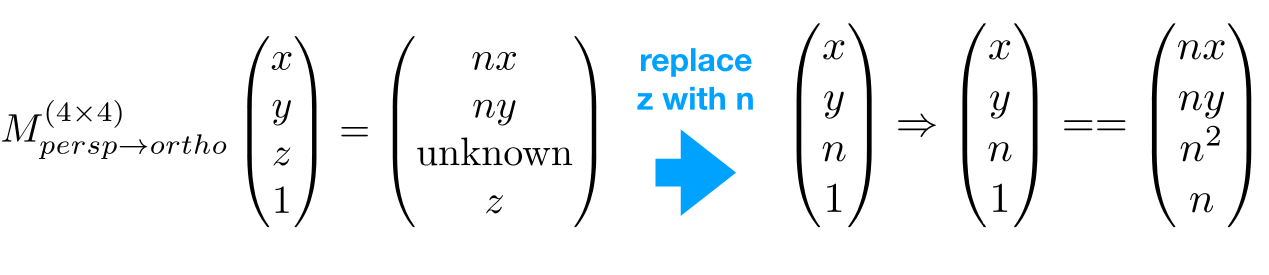

未知行第三行，可以表示为（AB为未知值）：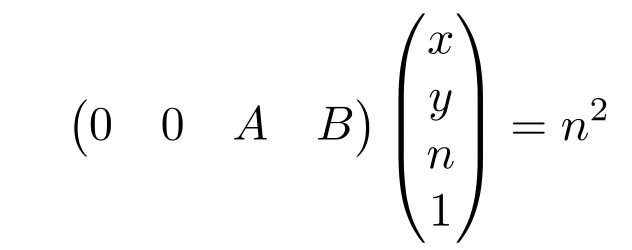


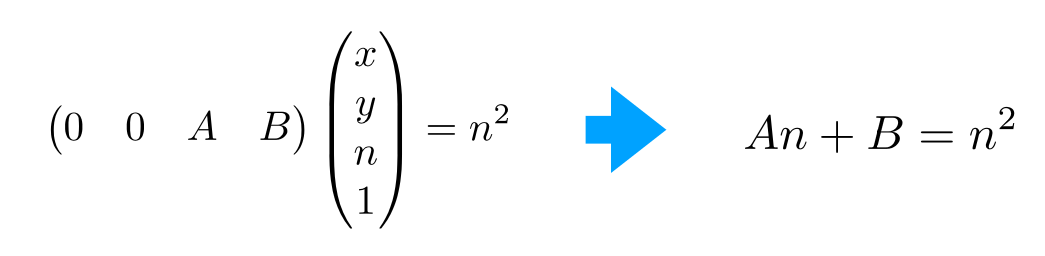
远平面中心点在缩放后是不变的，并且坐标同乘f：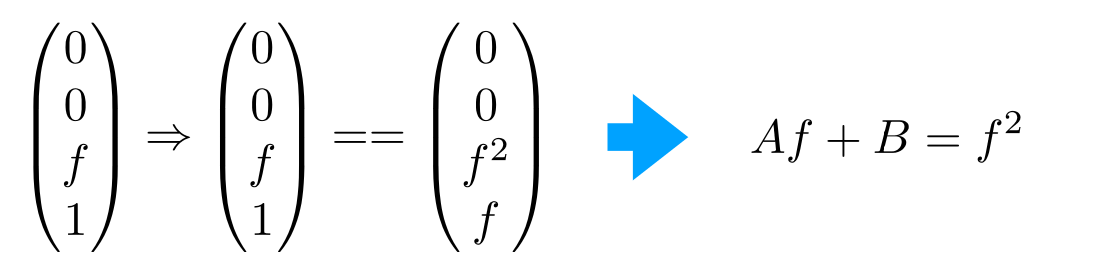

结合得到：

所以补充完第三行：

所以

最后得到这就是透视投影变换矩阵：

注意，这里得到的还是w = z 的齐次坐标
还需要做透视除法