Geometry Introduction：

几何分类：

2.显式几何implicit

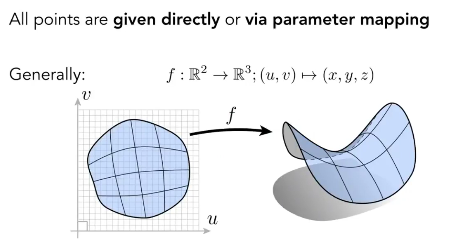
image.png
1、 所有点都显示的给出来，
2、 上图所示，用参数映射的方法表示，把UV所有点走一遍就知道这是个什么形状（马鞍面）
所以下面也是显式表示（只把所有UV都找一遍就知道模型）
image.png
显式表示与隐式表示优缺点刚好相反，

  • 好处在于快速找到哪些点满足这个式子（判断形状）。
  • 坏处则是难以快速判断点是否在几何体上，

    点云 Point Clouds

    image.png
    就是一个xyz的点的列表，当点云足够密的时候看起来就是一个面，多用于扫描点。

多边形面 Polugon Mesh

image.png
几乎是最广泛的表示，尤其是三角形面和四边形面

  • Triangle
  • Quard
  • N-Gon

Wavefront Object File OBJ文件格式
image.png
非常常用，就是一个文本文件，保存了

  • vertices 顶点 （v）
  • normals 法线 (vn)
  • texture_coordinates 纹理坐标 (vt)
  • 连接关系

    贝塞尔曲线 Bezier Curves

image.png
通过三个点确定一条曲线，初始点b0，结束点b2。确定曲线方式就是引入时间t的线性变换，b0到b1与b1到b2时间相等，确定两个时间点t记录的点b，连接两点得到新的线段，并确定在新线段的时间上点t记录的点b。通过t随时间线性变换，连接生成新线段点t记录的点b，得到贝塞尔曲线。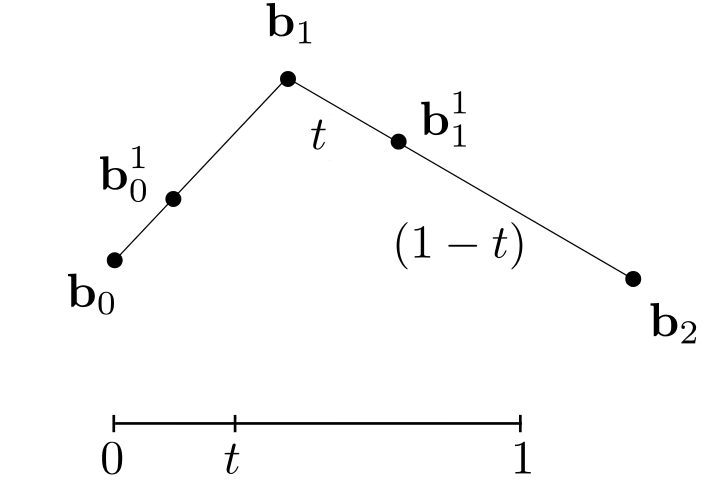
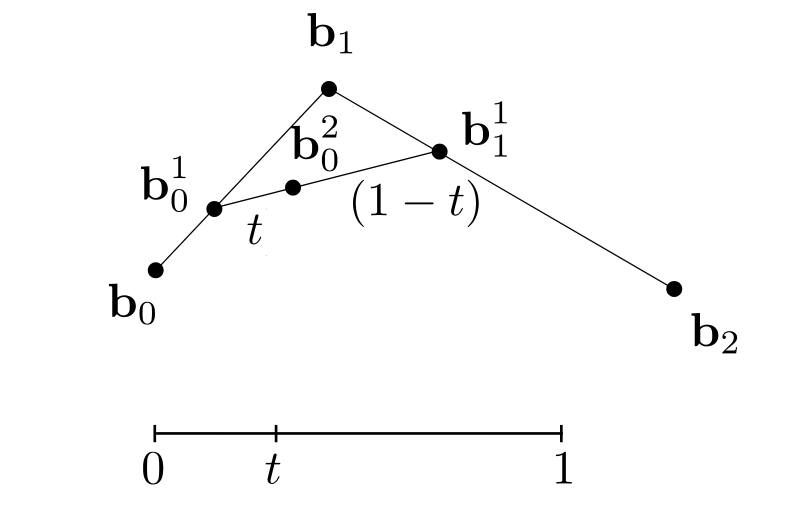
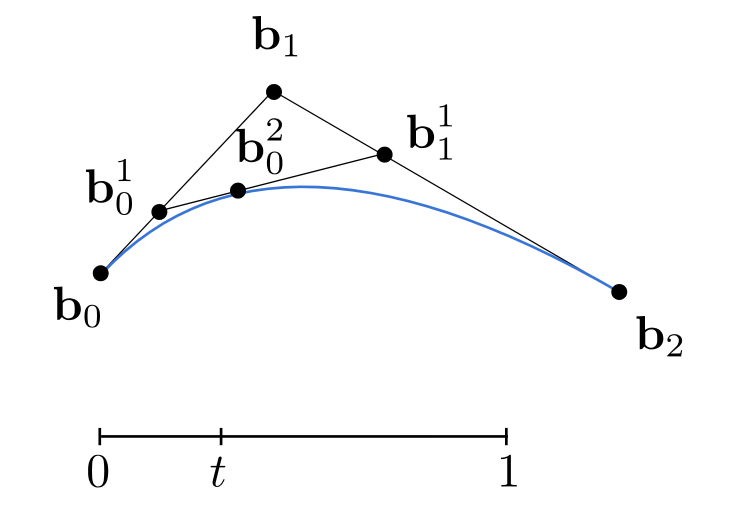
image.pngimage.png
image.png
假设t = 1/3， 那么b0b1上的1/3在b01，同理得到b11，连接b01和b11，再继续找1/3，得到b02，这时候递归到终止情况，b02的位置就是在整个贝塞尔曲线的t = 1/3位置处。
代数表示如图下：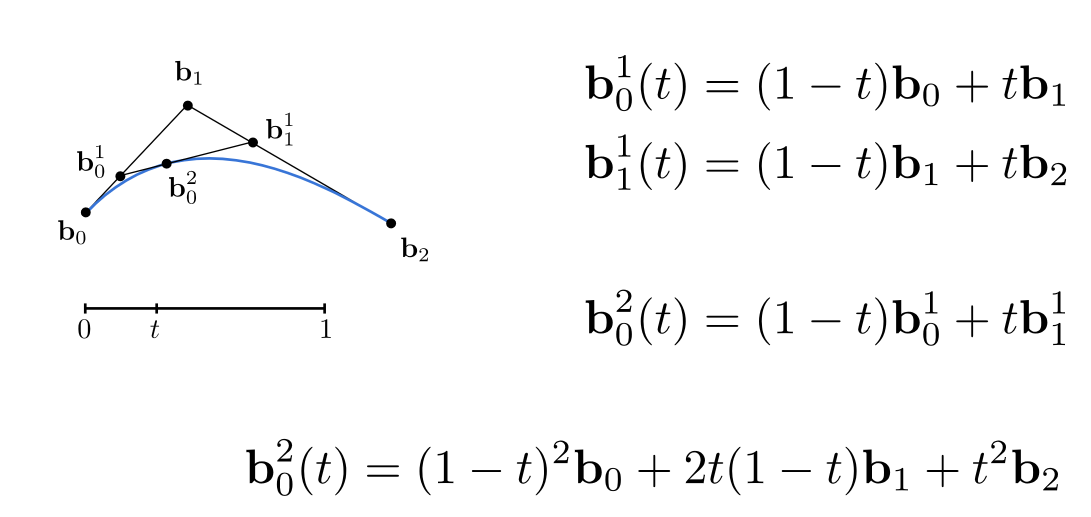
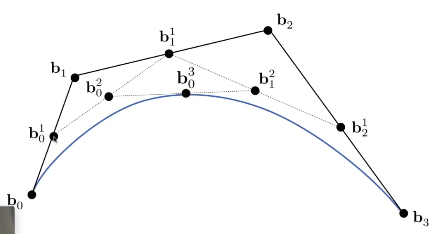
image.png
三次贝塞尔曲线 :::info 这里的3 只是因为是n次贝塞尔曲线，不是固定的 。 n次贝塞尔曲线（n个线段），有n+1个点， ::: image.png
同理，当t = 0.5
动画演示：
动画1221.gif
从上图可以知道这是一个线性插值过程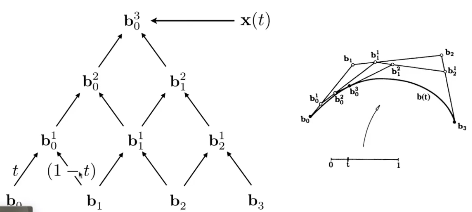
image.png

给定n+1个控制点，下标依次为0 1 2 … n
可以得到n阶的贝塞尔曲线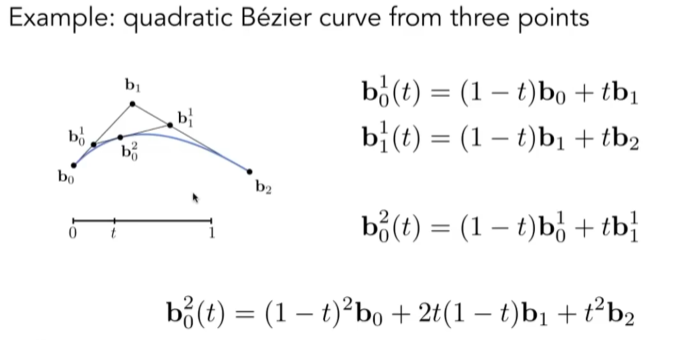
image.pngimage.png
（i= j）

最后的点是控制点的一个线性组合（伯恩斯坦多项式作为系数对给定控制点进行加权）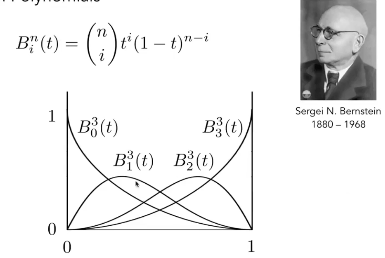
image.pngimage.png从n项中取i项
左图中，给定一个数竖线，在任何一个位置，与之相交的四条曲线值相加都等于1。相当于对1自己的n阶展开！
用组合的思维去解释就是：从3项中取0项，取1项，取2项，取3项，这四种结果概论之和等1

贝塞尔的性质

  • image.png
  • 仿射变换不变性，控制点仿射变换后绘制的贝塞尔曲线一样正确。
    • 投影不行
  • 凸包性质，convex hull
    • 凸包能够包围给定几个顶点的最小凸多边形。
    • 凸包，可以认为顶点是钉子，凸包就是橡皮筋箍住所有钉子形成的形状。
    • 贝塞尔曲线不能超过控制点形成的凸包。
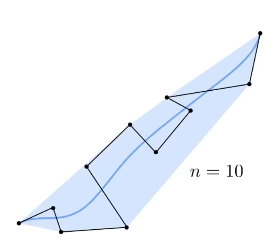
    • image.png

逐段定义贝塞尔曲线， piecewise Bezier Curves

经常是每四个控制点，定义一条贝塞尔曲线。 cubic 三次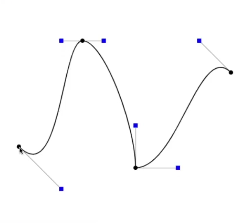
image.png
因为三次贝塞尔有性质

  • 曲线起点过控制起点且切线过p0p1，满足斜率t0 = 3（p1-p0）
  • 曲线终点过控制终点且切线过p2p3，满足斜率t1 = 3（p3-p2）

保证连续
c0 连续，值上连续
image.png
c1连续，一阶导数连续，切线连续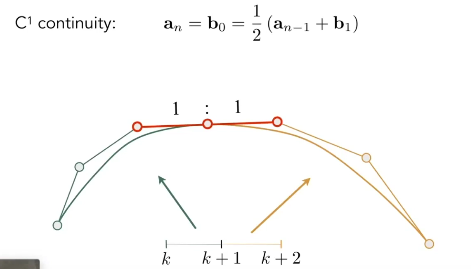
image.png
C2连续，二次导数连续，曲率连续
…

贝塞尔曲面

多条贝塞尔曲线，随时间线性变换生成的面（一个uv（时间）到空间的映射）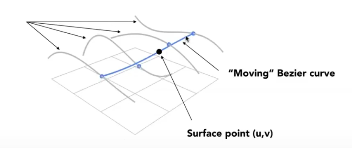
image.png

用贝塞尔曲线去得到贝塞尔曲面，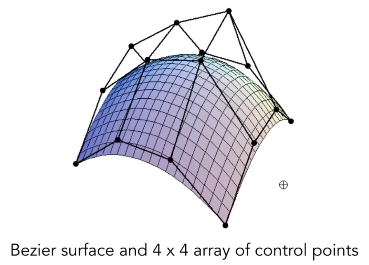
image.png
就是双线性插值。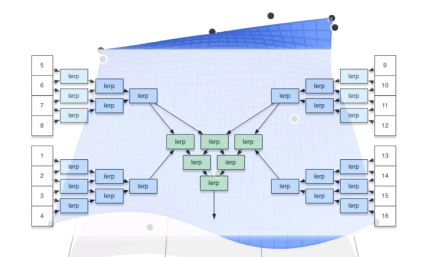
image.png
难点问题：不同曲面的边界拼合，
image.png utah茶壶壶身是一整个贝塞尔曲面