1.反走样:
Aliasing走样:
采样出现错误(Sampling Artifacts):锯齿、摩尔纹、车轮纹理等
Antialiasing反走样:
对图形进行模糊后,再次采样: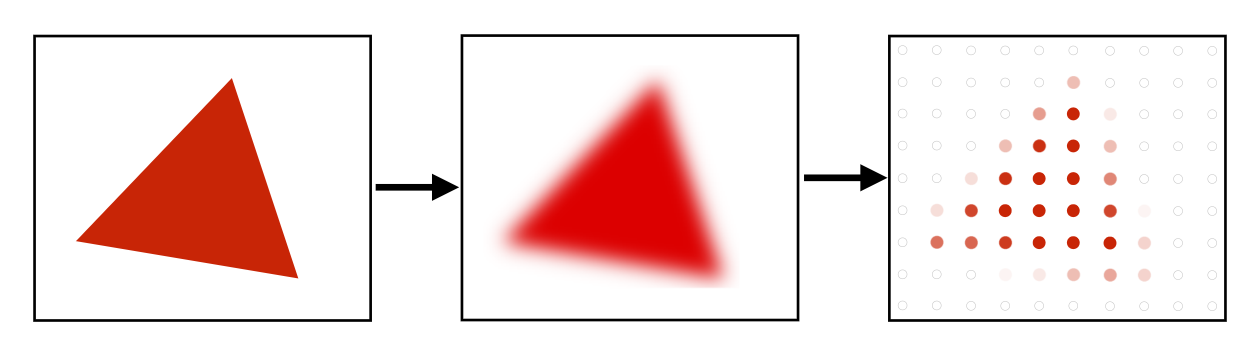
不能相反操作,那样是对走样进行模糊。
2.频域和时域:
时域、时域理解:
从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而永恒不变的就是频域。
举例:音乐
时域:音乐在时间内高低起伏变换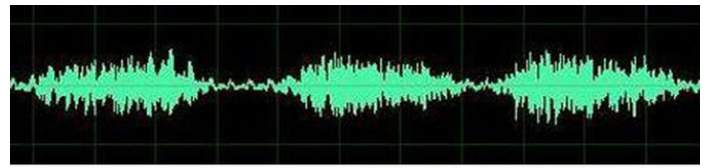
频域:音符(音符是不随时间变化的)
Frequency Domain频域:
周期是频率的倒数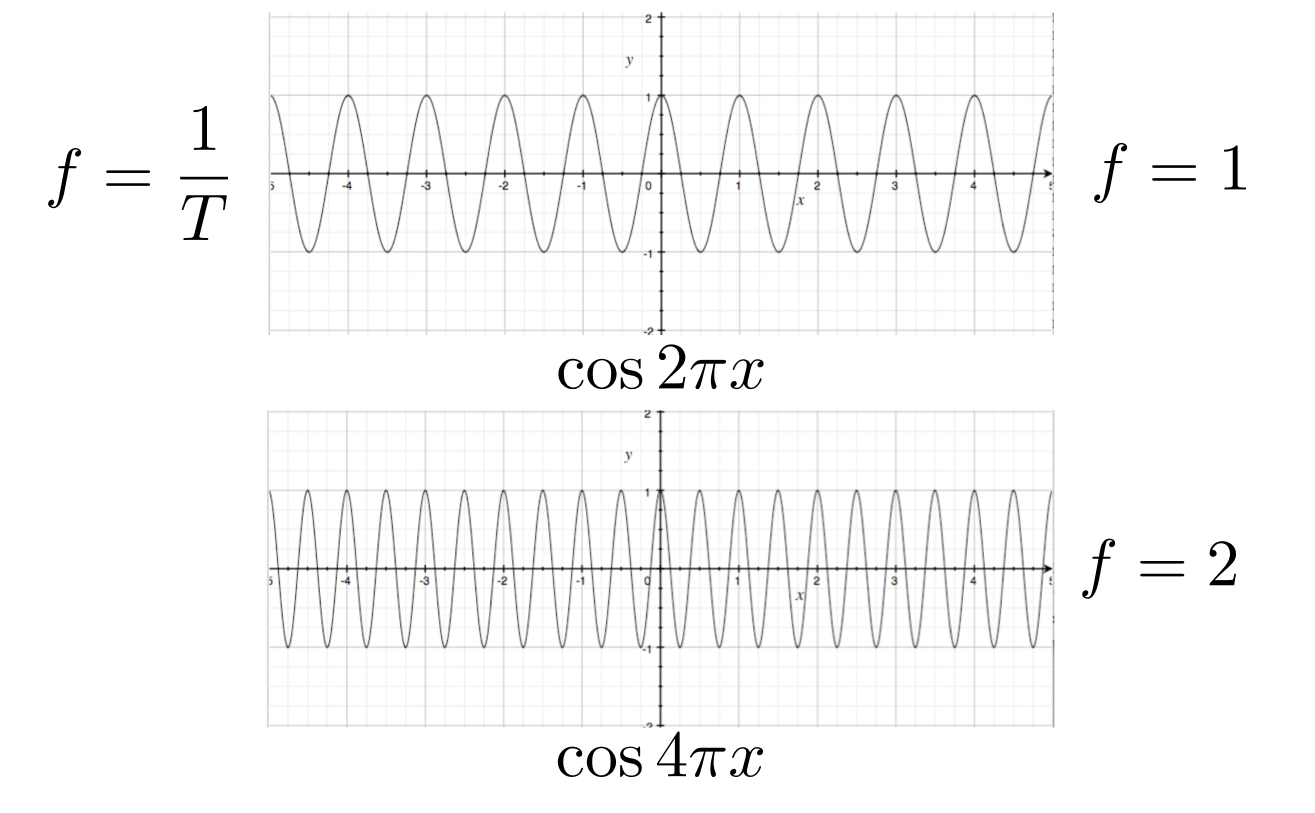
频域可以通过傅里叶级数展开: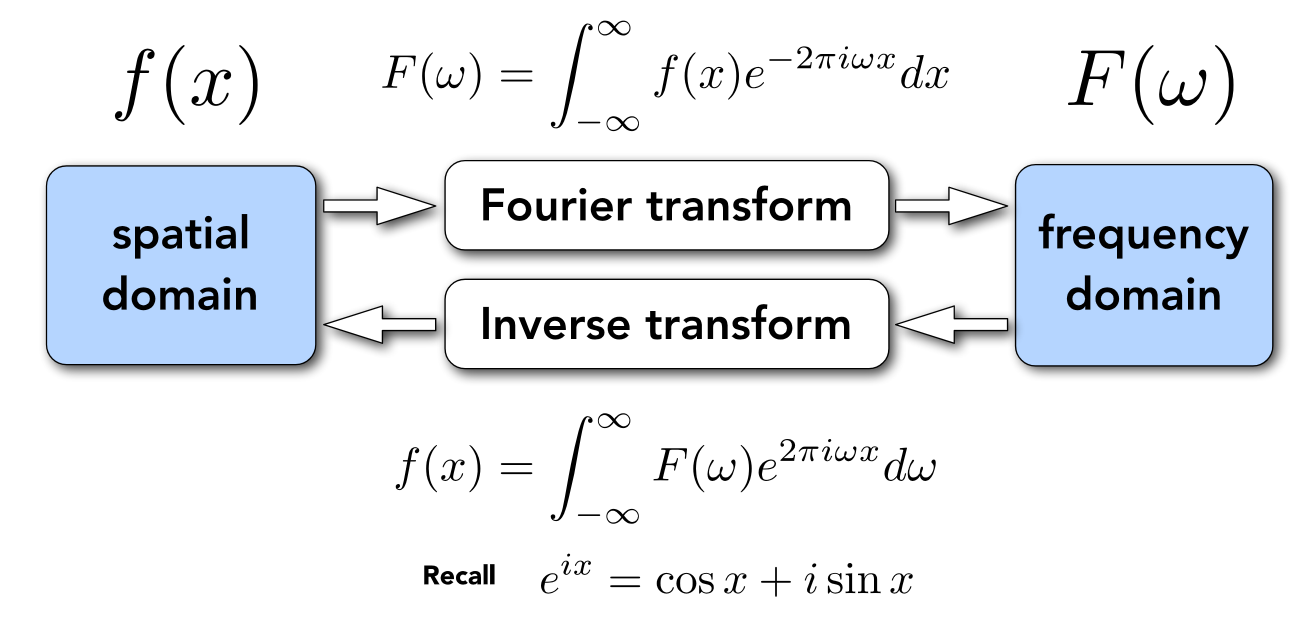
傅里叶变换和逆傅里叶变换:
一个函数f(x),经过傅里叶变换可以变成一个F(ω)
其实就是说,把一个周期函数通过傅里叶级数展开分解成不同的频率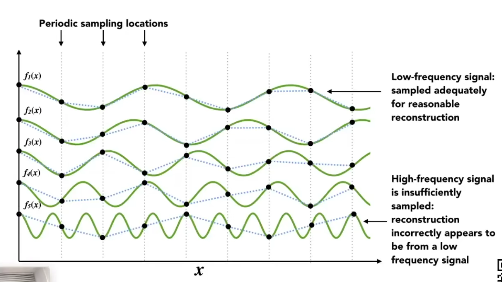
通过这个频率分析可以看出来,高频需要高频采样,否则就会走样。
走样的定义: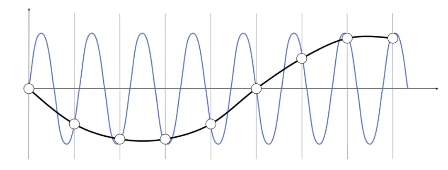
两个不同的函数,用同样的频率采样,我们无法区分它们。
Filtering滤波:
滤波就是对频域中的特定频率进行过滤。
当我们把一张图进行傅里叶变换(白:低频信息 黑:高频信息):
对频域上进行高通滤波处理,去除低频,得到就是边界信息。因为边界像素信息对比强烈,属于频域中的高频。当我们通过高通滤波把高频提取出来,就得到了图形中的边界信息。
对频域上进行低通滤波处理,去除高频,图像就会模糊。因为边界像素信息对比强烈,属于频域中的高频,当我们通过低通滤波把高频过滤调,那么边界就会模糊,图像就会模糊。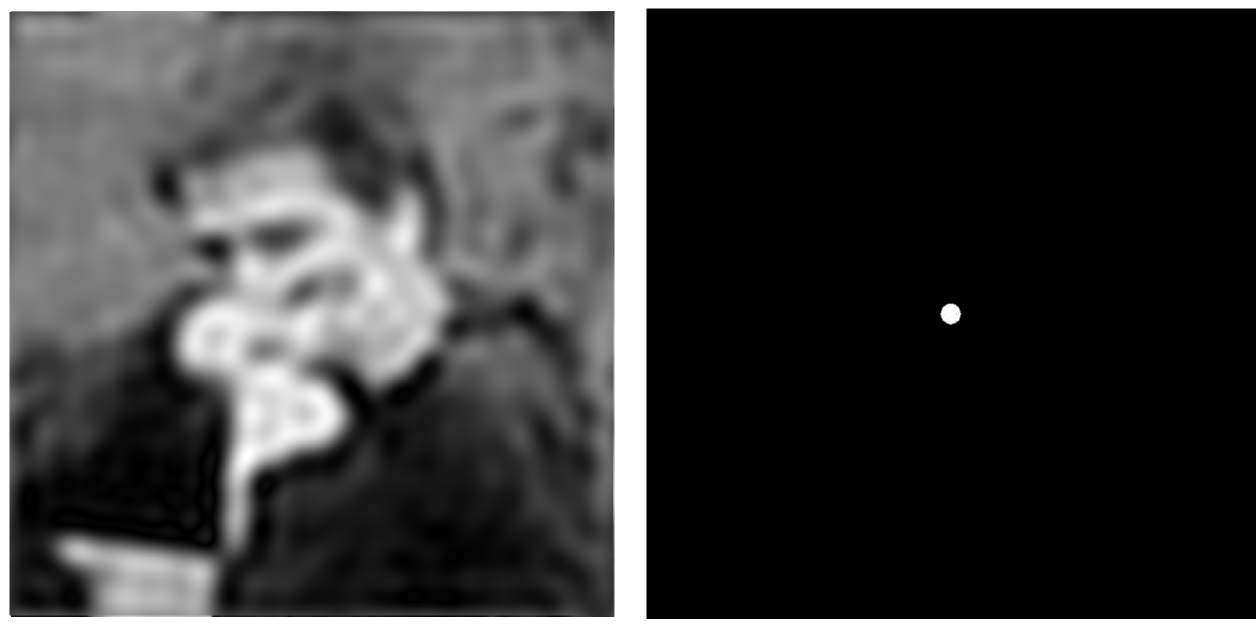
Convolution卷积:
Filtering = Convolution(= Averaging):卷积和滤波作用相同。
图形学中卷积的意思就是对像素周围的点取平均值。
例如:过滤器对signal进行乘积计算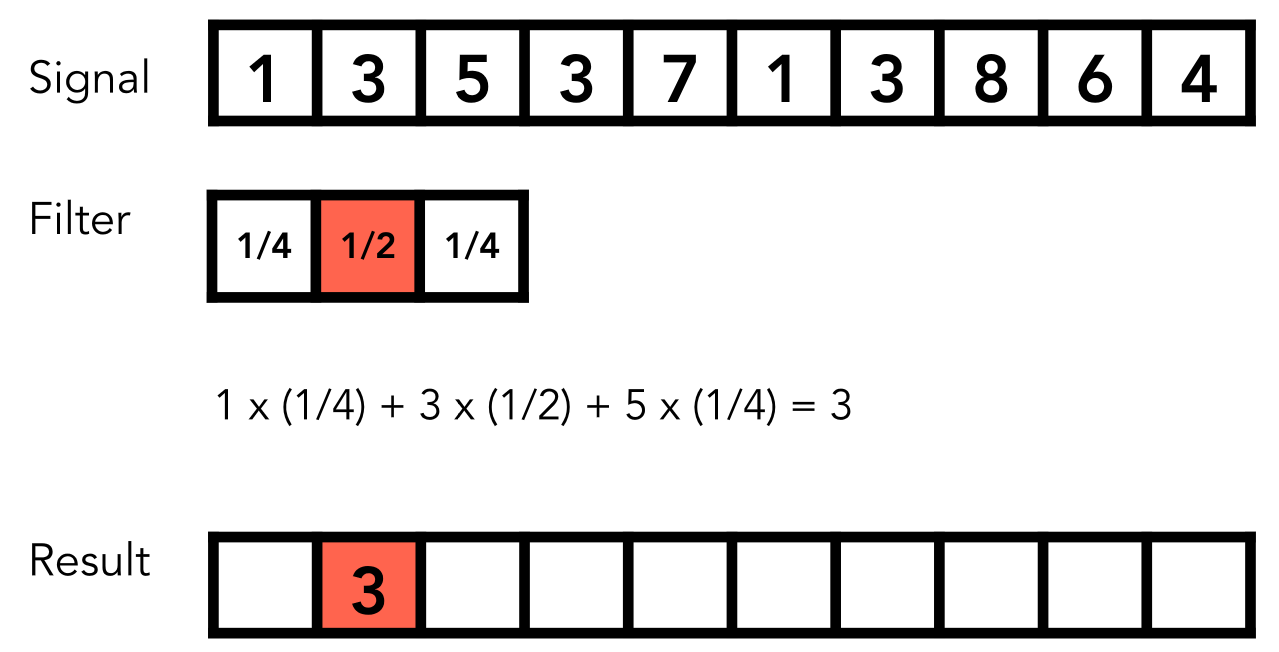
例如:对图片中每个像素点的周围8个像素进行求和,然后归一化得到一个9格像素的平均值。
采样:
采样就是重复原始信号的频谱(b在重复a的出现方式)
在时域上的卷积等于在频域上的乘积。反之亦然
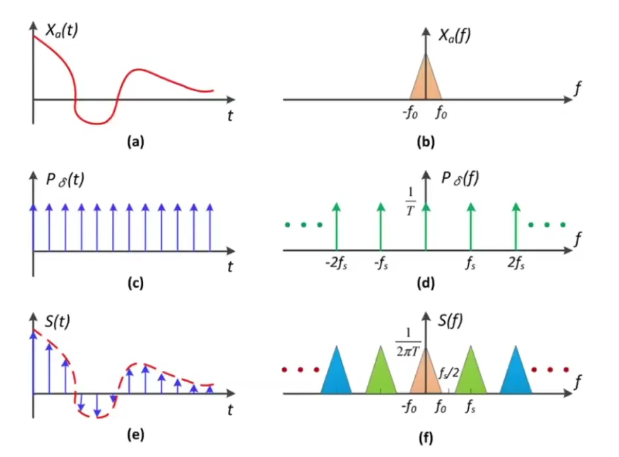
左边是时域,右边是频域。
c是冲击函数
- a * c = d
- b 卷积 d = f
- e = f
那么为什们会走样呢?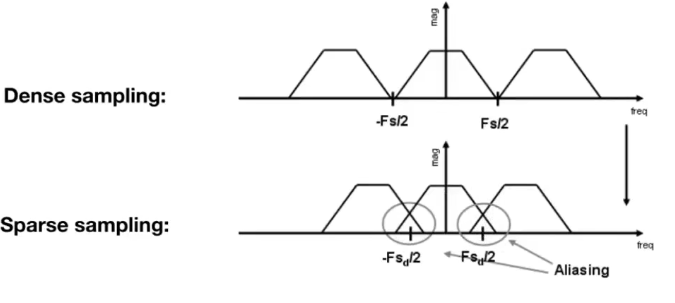
就是因为采样的间隔不够快引起了频谱上的混叠
Antialiasing方式:
根据采样性质,反走样就是:
1.提高硬件分辨率,进而采样密度。
2.让傅里叶变化后的内容变窄,也就是去除掉高频部分。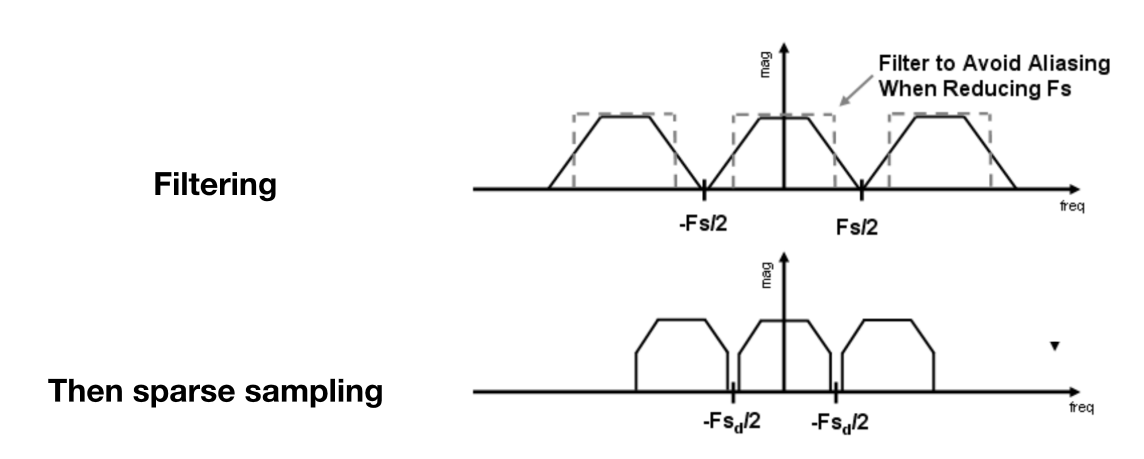
01 MASS:
对采样点进行分割: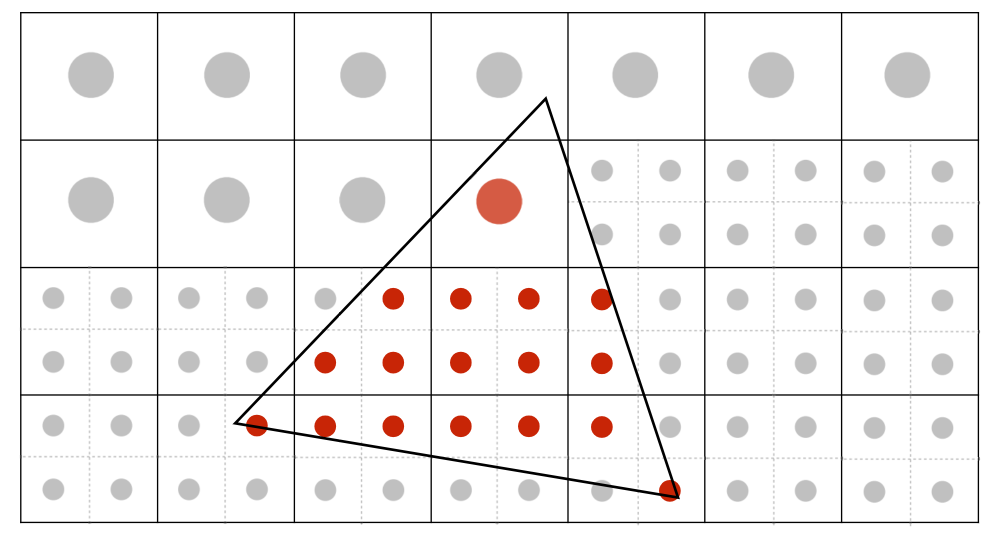
根据每个像素点中的不同采样点分析得出每个像素点中多少采样点才三角内,进一步得出比例(比例可以解为颜色的深度)。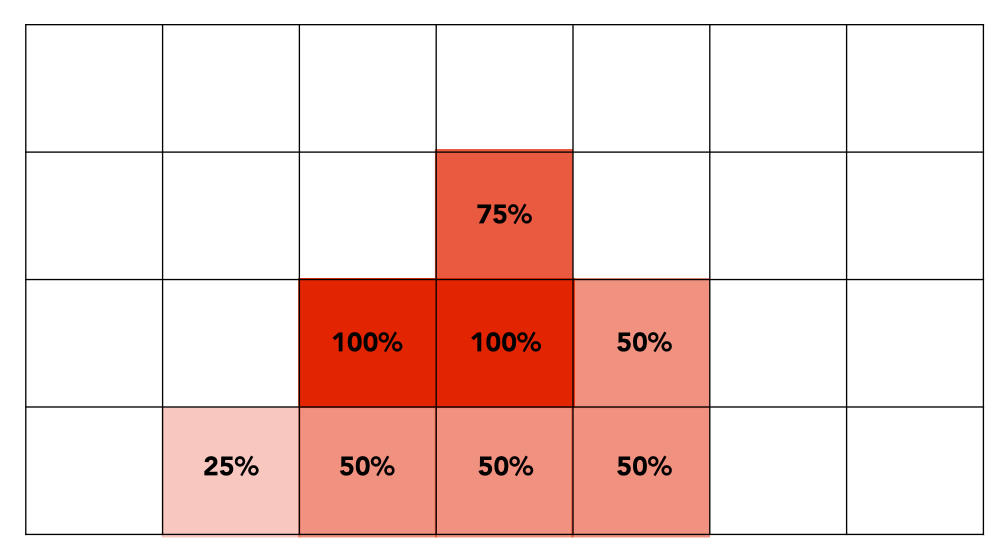
MASS的缺点就是会增加运算量。
02 FXAA:
03 TAA:
通过对该帧的上一帧进行分析,优化下一帧。(UE在使用)

