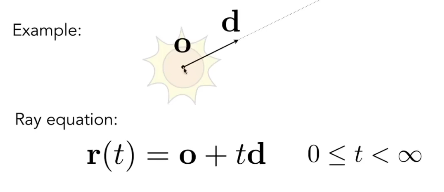
Ray Tracing
为什么要光线追踪?
因为光栅化有些问题解决不好 ,主要是全局效果,global effects
- 软阴影
- 光泽度反射效果
- 光线多次弹射产生的间接光和反射材质
光栅化和光线追踪
显示的两种方式:
 |
 |
|---|---|
| 光栅化是一种近似的方法 - 质量比较低, - 但是速度快, - 可以real-time |
光线追踪是一个准确的方法 - 质量高,符合物理规律 - 但是速度慢,大约1w CPU小时渲染一帧 - 一般offline(现在也可以实时了) |
什么是光线 Ray Light
对于光线的三点假设
- Light travels in straight lines (though this is wrong)
- Light rays do not “collide” with each other if they cross (though this is still wrong)
- Light rays travel from the light sources to the eye (but the physics is invariant under path reversal - reciprocity光线可逆性).
“And if you gaze long into an abyss, the abyss also gazes into you.” — Friedrich Wilhelm Nietzsche (translated)
所以找到光路就是光线传播渲染最重要的事情。所以事情可以变成从摄像机发射光线到场景,然后一直弹射,寻找可以弹射到光源的光路,计算光路上的颜色吸收和能力损失。
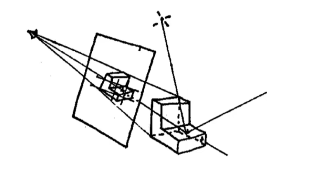
Ray Casting 光线投射-直接光
apple 1968
- 从摄像机投射光线到成像平面
- 对于每一个像素,从摄像机到它连一条线穿过像素打到场景中去
- 得到一个
击中点
- 再从
击中点连线到光源,判定是否被遮挡,是否属于阴影区
- 如果对于光源也可见,那么就得到摄像机-成像平面-击中点-光源的光路
- 然后计算着色
几点假设
- 眼睛是个小孔,一个点 eye_pos ,针孔摄像机 (如果是有大小的摄像机,在path tracing 路径追踪中)
- 光源也假设是一个点光源
- 对于场景中的物体,认为打到它们之后,会进行完美的折射和反射
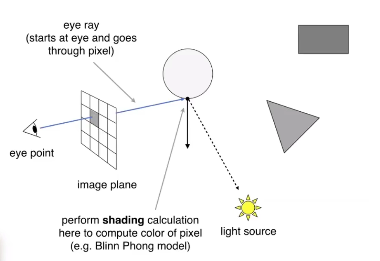
至此,光线还只是反射弹射了一次,如何让光线可以弹射很多次呢?那就是Whitted风格
Recursive(Whitted-Style) Ray Tracing-直接光+1次间接光
能很好的处理折射和反射的问题。(相比于光栅化)
计算思想
对于一个像素,把进入它的多条光路加权求和(蓝色点线,能量衰减)。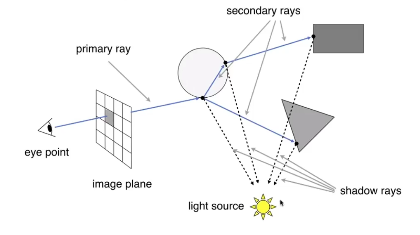
拓展阅读:如何计算一条光线
求交点 Ray-Surface Intersection
光线,就是数学上的射线,所以需要两个数据
- 起点
- 方向
求交点就是另一条光线的起点
与球的交点
点p满足在光线,同时满足在球上 p = r(t)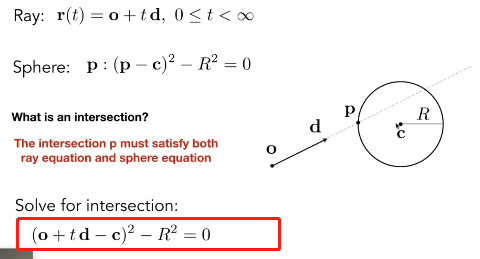
就是解一个二次函数
推广:与一般隐式表面的交点
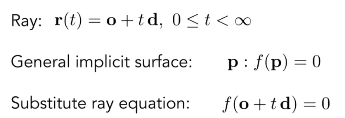
求解f得到t的值,并且要求
- 根是正数
-
与一般显式表面的交点
主要是指的polygon(tri)
可以判断物体是否在模型内外(一个交点代表一次内外交换)(不考虑相切的情况),从一个点往任何一个方向发出一条射线, 如果在模型内部,则与模型有且只有奇数个交点
- 如果在模型外部,则与模型的交点数是偶数个。
最朴素又很慢的方法:从屏幕上每一个像素n发出一条光线计算与模型的每一个三角形m的相交情况。(结果要么是0个要么是1个,不考虑平行的情况)
与一个三角形求交点
与三角形求交的计算步骤:
- 光线与三角形平面是否有交点,
- 交点是否在三角形内
定义一个平面:一个法线方向+一个平面上的点 (点法式)
p’到p垂直与法线N,点乘 = 0,
把光线的方程带入点P可以得到t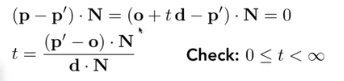
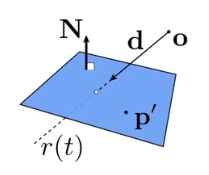
同时就得到了P点,然后判断P是否在三角形内
Moller Trumbore MT算法 加速
用重心坐标描述点P: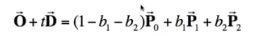 (系数之和为1,p点才在这个三角形所在的平面上)
(系数之和为1,p点才在这个三角形所在的平面上)
未知量是t b1 b2, 已知量是向量的三维数值,所以就是解三元一次线性方程组,方程个数与未知数个数相同,用克拉默法则解:
只要b1 b2 还有1-b1-b2是非负的,并且t是非负实数那么就在三角形内
AABB包围盒Bounding box 加速与三角形表面模型求交
前面的方法只是加速了与三角形求交的速度,但是我们要知道k个模型是否被看到仍然要计算kmn次,非常大的计算量,如何加速?
包围盒Bounding box

简单逻辑:如果一个光线连包围盒都无法击中,那么更加不可能击中物体本身
三维中最常用的就是长方体(三个不同对面形成的交集)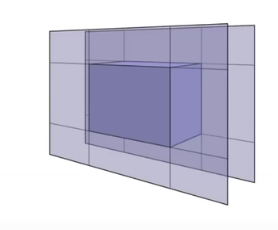
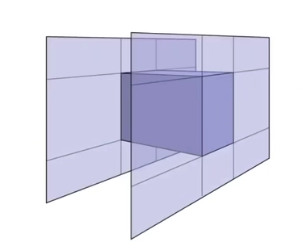
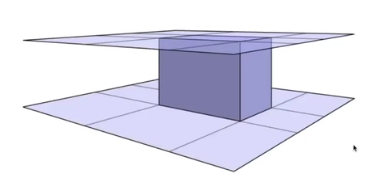
通常用轴对齐的包围盒 Axis-Aligned Bounding Box (AABB) 轴对齐包围盒
每个轴肯定是一个在正交标准平面中,因为用aa会很好计算,比如以垂直于x轴的平面为例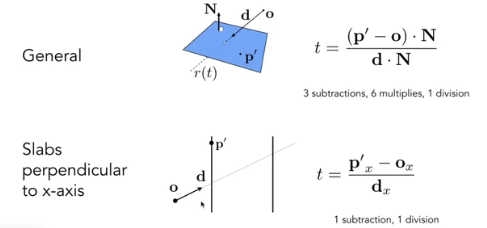
按照点法式得到的平面方程计算交点t的解析式,如上图
如果是Y-Z平面,则可以优化成下半部分的式子,直接用x分量即可计算。
光线与包围盒求交点
2D简化情况(时间可以是负数)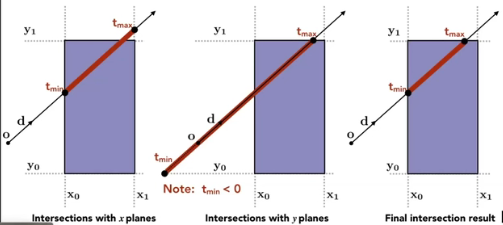
左图:光线与左右对面相交的t
中间:光线与上下对面相交的t
右图:对前两部得到的t做一个交集,就得到了最终的结果t
推广到三维一般的情况逻辑
- 光线要进入所有对面,才是进入了盒子
- 光线只要离开了一个对面,就离开了盒子
最后的结果就是:
在时间最小的末端进入盒子,在时间最大的起始段离开盒子
当且仅当iff
- 光线在盒子里待了一段时间
如果
- 则没有交点,盒子在光线后面
如果
- 则光线起点在盒子里,一定有交点