内容

蒙特卡罗积分 MonteCarlo Integration

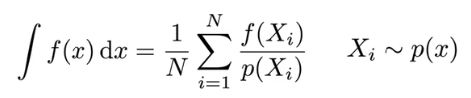
image.png
概念就是在函数上随机采样

  • 样本越多，越准
  • 在x上积分就得采样x

    WHY

    我们想要计算一个定积分（数），但是函数太复杂，不好写解析的不定积分（表达式）。那么怎么求这个定积分呢？我们只想得到一个数。

    WHAT

    :::info 黎曼积分Riemann Integral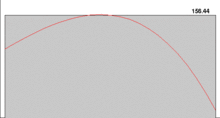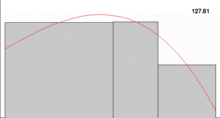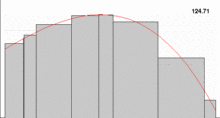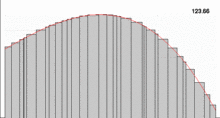
    16. Ray Tracing 4 - 图2
    把求区间的面积变成求各个分割的小长方形面积之和 :::

随机的方法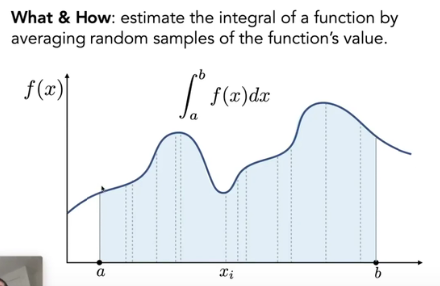
image.png

假设用一个固定的均匀采样函数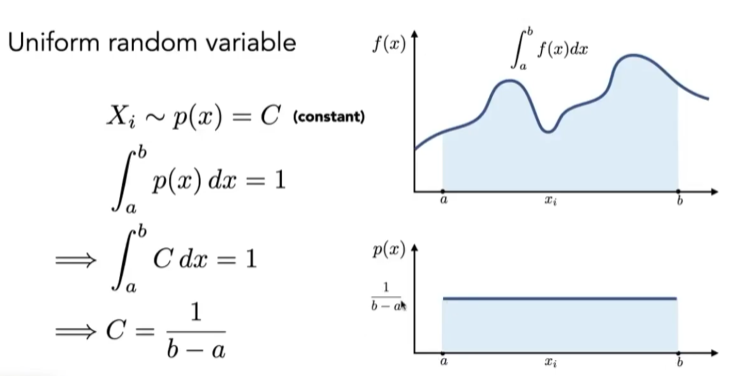
image.png

  • 每次采样一个x，得到一个长方形面积宽= ab，高 = f（x）
  • 多次采样
  • 结果平均起来

image.png
其实就是px = 1/（b-a）

HOW

定义一个定积分表达式
设置一个采样概论分布函数p（x），用它来得到采样点X
然后计算结果Fn
image.png
其实上面WHAT中的步骤就是对应这里随机变量是一个均匀采样的情况

Path Tracing

首先来看看之前说的Whitted style 的ray tracing 的一些问题
然后Path Tracing 再来介绍如何解决这些问题的。

Whitted-Style Ray Tracing Problem

  • 遇到镜面反射则反弹光线
  • 遇到漫反射停止反弹光线

问题一：无法处理 Glossy Reflection

image.png

问题2：无法反弹漫反射的间接光

color bleeding 效果
image.png

渲染方程替代 whitted-style ray tracing

whitted-style ray tracing是错的
渲染方程是对的，但是它有两个非常困难的问题

  • 在半球面积分 - 蒙特卡洛方法解
  • 递归计算 - 俄罗斯赌盘RR算法

1 - 蒙特卡洛-半球面积分-简单直接光照情况

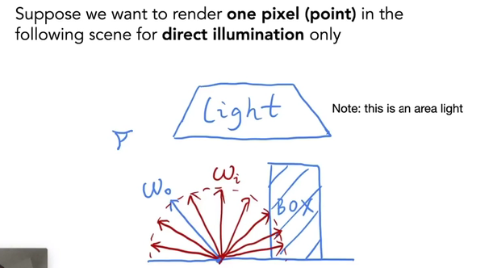
image.png
求一个点的直接光照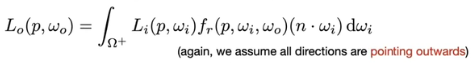
image.png
这种简化情况下，没有递归，没有自发光，单纯做定积分
image.png
均匀的在半球上采样角度如上

对于一般直接光照情况的采样：
image.png
这个函数得到的是一个出射光线radiant，这条光线从物体射向眼睛。
到此，这就是全部的只考虑直接光照的PathTracing算法。

2 - 从直接光照递归到全局光照-递归问题

只需要修改一下直接光照情况的采样：
image.png
新添加的这部分表示，把当前物体看作眼睛，寻找一条从第二个物体Q到达当前物体P的radiant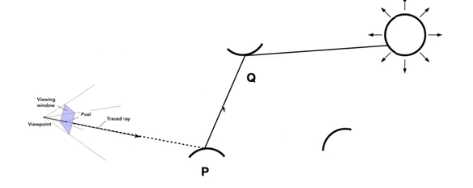
image.png
然后物体Q又会递归寻找一直递归到光源为止

随之会带来一些问题需要解决：

光线数量爆炸- N=1的蒙特卡洛积分

Explosion of rays as bounces go up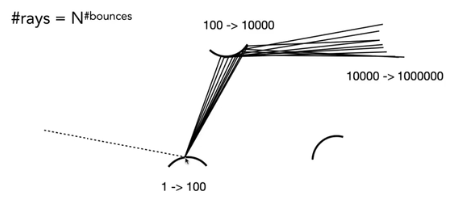
image.png
iff N ==1 的时候，才不会出现光线数量爆炸，对应代码就是：
image.png
这就是我们说的路径追踪（N=1），因为确实是一条路径线而不是树了。
N != 1 的情况就是分布式光线追踪，这个用的不多，真的会出现爆炸
N=1由此会带来很多的噪点，但是可以解决，那就是用多条path
image.png
因为一条光线是很noisy的，但是多条穿过同一个像素的path求平均就可以平滑
所以修改一下代码
image.png
这个其实也类似蒙特卡洛积分，只不过这里的N是从一个像素里面均匀取得N个发射点
N是可控的。

递归终止条件- 俄罗斯轮盘赌 RR

递归问题

  • 能把一个问题转化为另一个问题
  • 能停下来

第一个问题在上面解决了，现在是第二个问题，
现实生活中光线是无限次数反弹的，如果强行截断反弹次数就会导致能量不守恒

怎么解决？俄罗斯轮盘赌
image.png
让光线在一定的条件下停下来，而不是一直追踪
image.png

  • 首先，我们期望得到的结果还是Lo，
  • 但是，我们用一定的概论P去发射光线，得到的结果Lo/P
  • 另外的1-P的概论得到的是0，不发射光线。

最后我们仍然可以得到一个期望 E= Lo :::danger 期望，可能是有噪声的，但是结果肯定是对的 ::: 于是再次修改代码，添加递归的终止条件
image.png
至此，这已经是一个正确的path tracing的算法了

采样光源：提高渲染效率，降低SPP

但是效率很低，在low SPP的情况下噪点很大
image.png
原因就是发出path的N能打到光源的概率问题，尤其是像下图中光源很小的时候，就很难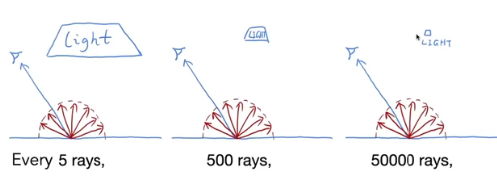
image.png
所以每个着色点是均匀往四面八方采样就会导致很多光线被浪费掉
最直接的解决办法就是在光源上进行采样（有点像传统的Bliinphong模型的感觉了，连接光源和着色点思想）
但是这里改变的是采样pdf

简单情况-直接光照

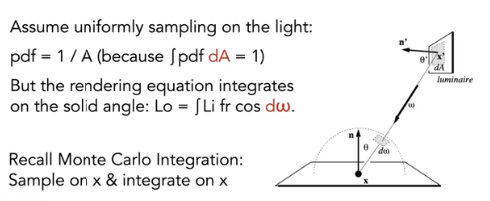
image.png
因为直接在光源上采样了，所以就要在光源上进行积分。换句话说就是要对dA进行积分而不是dω
进一步说就是要找到dA和dω的关系，那就是把dA分解一个与连续方向垂直的面，然后计算一个立体角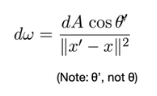
image.png注意这个角度是连线与A法线的夹角
接下来就改写方程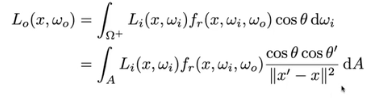
image.png
蒙特卡洛积分还需要一个概率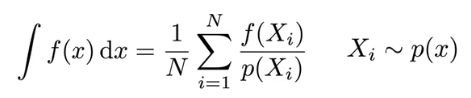
image.png
因为我们是在A上均匀采样所以每个点的概论都是1/A
到此，就完成了积分域的转换

之前我们是盲目地往空间发射光线，accidentally 打到光源，现在我们直接往光源方向发射光线
（这个还是解决简单情况——直接光照的问题）

关于路径追踪整体个人理解

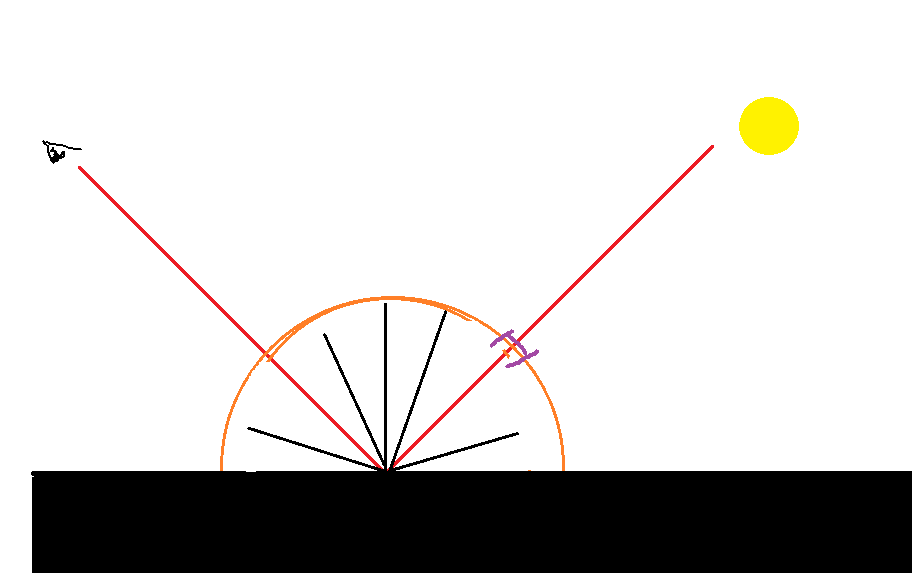
image.png
红色路径为直接受到光源影响的路径，所以对该路径的追踪是通过蒙克卡罗积分对光源光线穿过的立体角进行积分，这里只有一次弹射，所以不需要RR来停止。
黑色路径为追踪周围光线路径，对这些路径追踪是通过蒙克卡罗积分对周围光线立体角进行积分，因为这里路径会多次弹射，所以需要RR来停止。
蒙特卡洛积分中只计算一条光线的反射，即N=1，这样在反射中不会发生指数爆炸。但为了结果更加准确，会从像素采样处发射多条路径，最后求均值。
改变PDF：概率分布函数针对光线采样，如果不考虑直接光间接光，那么采样光线路径将分布均匀，如果引入直接光间接光，则会增加直接光采样频率分布，减少间接光，相当于优化采样次数。
这就是说明一个像素的采样受两部分影响，直接光跟间接光。