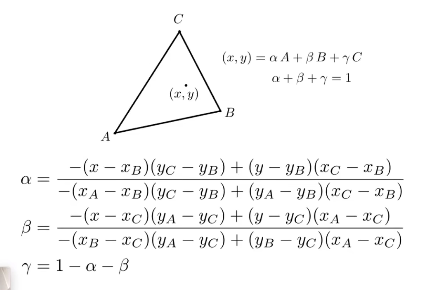1.插值概念解理解：

插值：插值指利用已知的点来“猜”未知的点，图像领域插值常用在修改图像尺寸的过程，由旧的图像矩阵中的点计算新图像矩阵中的点并插入，不同的计算过程就是不同的插值算法。
单线性插值：
就是求一个区间中的值，例如求P1跟P2中间P的值，P1到P2的区间是线性过渡的。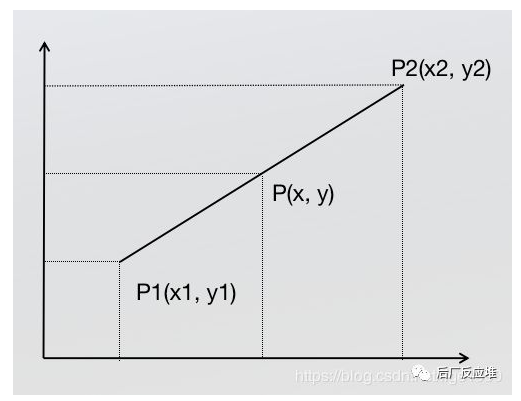
image.png
双线性插值(Bilinear）：
在图形学中，双线性插值就是求四个点形成的过渡区域中某个点的值（即需要两个方向的过度变化）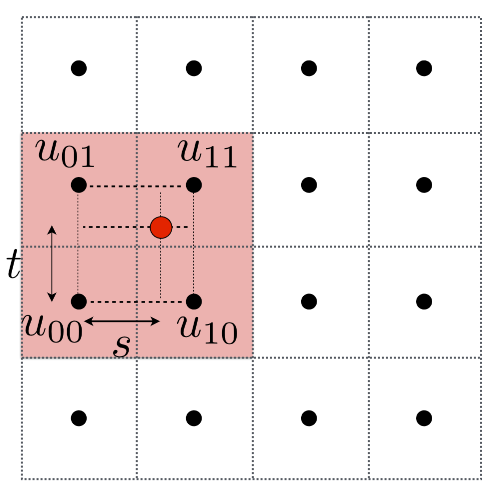
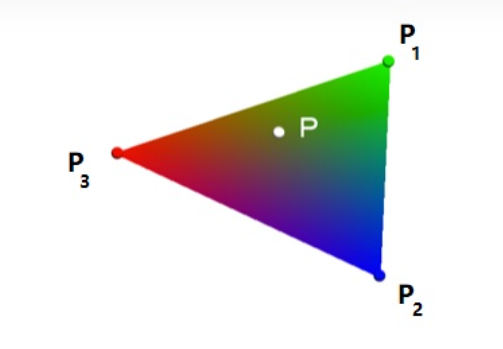
image.png

2.重心坐标：

上节课讲到了纹理映射，那么很重要的问题就是三角形内部的点和像素如何进行属性插值，这里的方法：重心坐标 barycentric coordinate

三角形插值：

在重心坐标坐标之前，首先要对三角形进行插值。
为什么需要插值

  • 我们的属性值是指定在三角形的顶点上（即线性插值区域的起始和结束），需要知道其内部点和像素的属性值
  • 并且需要三角形内部区域平滑过渡的值

什么是重心坐标（此处只考虑三角形）？

重心坐标是由三角形顶点定义的坐标。

  • 三角形上的任一顶点p(x,y)都可以用三个顶点的线性组合表示：p=w1a+w2b+w3*c
  • 且系数之和为1：w1+w2+w3=1 (只有系数之和为1，p点才在这个三角形所在的平面上)
  • 当满足三个系数都为非负数时，该点在三角形内部
  • 可以看出，重心坐标是齐次坐标的一种

这三个系数所表示的坐标（w1,w2,w3），就是该三角形上p点的（归一化）重心坐标。

  • 插值举例：假设三角形顶点的三个颜色C1，C2，C3，那么p点的颜色就是 Cp=w1C1+w2C2+w3*C3

  • image.png

    重心坐标定义：

    定义一：
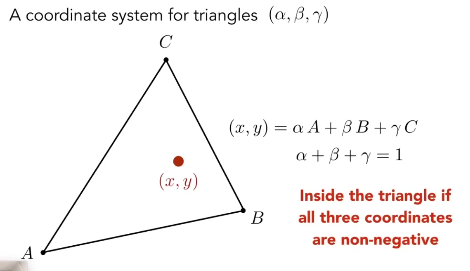
    image.png
    三角形中任意一个点的坐标可以用三个顶点的线性组合得到，只需要满足条件

  • 三个系数相加 = 1 ，（因此其实是两个未知数）

  • 三个系数都是非负的（如果不限制的话只能说明点在ABC平面内，不一定在三角形内）

把三个系数拿出来作为一个坐标来描述点的位置（与ABC的坐标系无关）

由此，我们知道A的重心坐标为(1，0，0)，

定义二：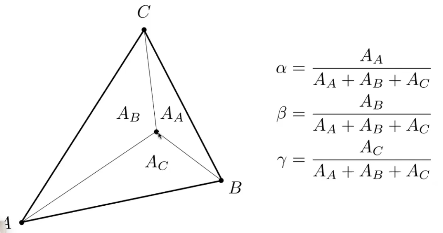
image.png
三角形内任意一点，我们可以通过面积比得到重心坐标
所以这为什么叫做重心坐标：重心位置重心坐标就是（1/3,1/3,1/3）

计算方法：
image.png

重心坐标与属性插值

上面介绍了重心坐标用来计算任意点的坐标，如果重心坐标应用在属性上，就可以求得任一点的属性。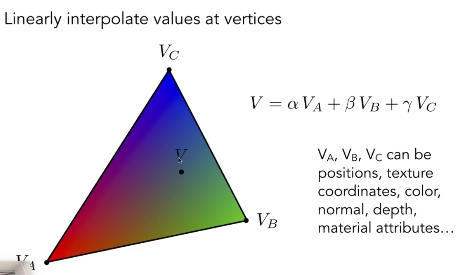
image.png
重心坐标在投影的时候，会有问题，应为它不具有投影不变性。
三维空间中V点求得的重心坐标，与把三角形投影后再求的的V点的重心坐标很可能不同。
所以三维中求得的重心坐标只用于三维空间

以深度举例
从三维空间中的物体，投影到屏幕，那么投影了的三角形内部某一点深度值可以是

  • A、投影了的三角形的顶点的深度值，进行插值后得到

也可以是

  • B、逆变换转换为3D空间中的三角形中的一点，用顶点的深度值进行插值得到

B才是对的，A是错的。

3.纹理贴图走样：

这里定义一个纹理像素的概念，也叫做纹素：texel ，指的是纹理的一个像素的大小。

贴图大小与像素大小不匹配：

当贴图大小密度与像素大小密度不匹配，例如贴图小，而像素密集，那么就会产生锯齿。
为了解决这种走样，目前主要采用这三种方法：

最近邻法(Nearest Interpolation)：计算速度最快，但是效果最差。
双线性插值(Bilinear Interpolation)：双线性插值是用原图像中4(22)个点计算新图像中1个点，效果略逊于双三次插值，速度比双三次插值快，属于一种平衡美，在很多框架中属于默认算法。
双三次插值(Bicubic interpolation)：双三次插值是用原图像中16(44)个点计算新图像中1个点，效果比较好，但是计算代价过大。

image.png

远处纹理过于密集：

当在采样过程中，如果远处纹理过于密集，那么会在一个像素上有太多纹理信息，产生摩尔纹。本质上就是一个像素内的纹理太多信号上表示就是高频信息太多，而采样频率不匹配。
image.png
解决方法首先就是之前提到的MASS，去除高频信息。但这样的计算消耗会非常大。
image.png
第二种解决方法就是MipMap：
mipmap = image pyramid 图像金字塔
支撑 fast approx square必须是正方形！ 范围查询
image.pngimage.png
27 = 128

额外引入的存储量是多少？4/3
也就是说，所有新增的mipmap只是增加了原图的1/3（因为MipMap简化了原图的像素信息）

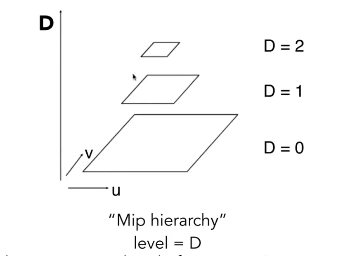
Mipmap实现原理：

首先，要知道 屏幕中的一个像素移动，在对应的UV上有多大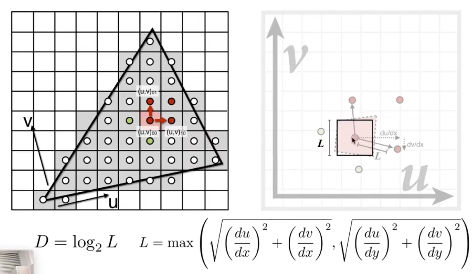
image.png
这里取近似，一个最大的正方形边长L，
这便是一个像素 对应的UV上长度，所以，

  • D=0，L=1 ；用第0层的mipmap，1个pixel覆盖1个texel。
  • D=1，L=2；那么一个pixel覆盖原始2*2 = 4个texel，一个pixel占据4个texel。刚好是第1层mipmap的结果。
  • D=2，L=4；那么一个pixel覆盖原始4*4 = 16个texel，一个pixel占据16个texel。刚好是第2层mipmap的结果。
  • 。。。

也就是查询在第几层，内部都是1个pixel覆盖1个texel。得到的是平均属性值。最终目的是为了实现像素与纹素的匹配。
可视化的层级查询结果：
image.png
这里有个问题就是不是很连续。容易生成缝隙。
因此，可以进行一个三线性插值。Trilinear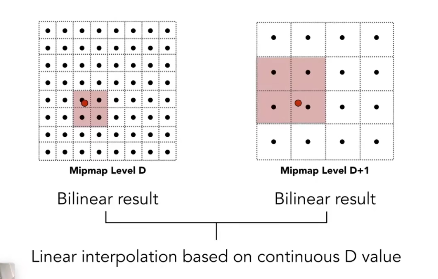
image.png
这就是先进行双线性插值（层内平滑），然后把结果再上下插值。（层间平滑）
可视化结果：
image.png

Mipmap的局限性：

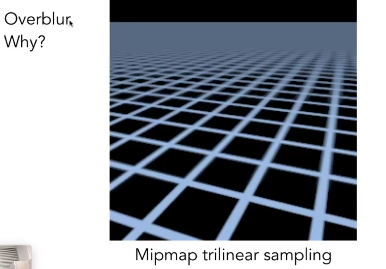
image.pngimage.png
回到一开始的问题，如果512x的超采样时正确的结果，而mipmap却把远处模糊掉了，这是为什么？

可能是三线性插值导致的过度模糊，这个可以用各向异性过滤来解决：Anisotropic Filtering
image.png

各向异性过滤

那么什么是各向异性过滤呢，其实就是增加了长条形区域的mipmaps。当屏幕像素对应到纹理坐标上时，形状可能是长条形，不再是正方形，例如右上方的长条形。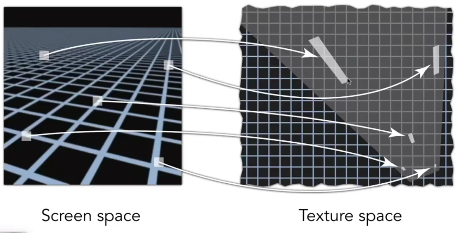
image.png :::info 各向异性，就是在各个方向上表现不同；相对于各项同性。
它考虑了方向性 ::: image.png
Mipmap在这张Ripmaps上只相当于是对角线范围的数据，
但是，数据量多了3倍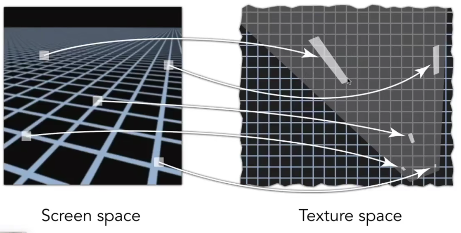
image.png
屏幕空间的一个像素，在纹理空间是一个长条形区域，能够快速得到更好的范围查询结果，
mipmap只能支持矩形区域的查询
但是对于左上角这种斜着的长条区域还是不好查询。
还有其他方法，比如说EWA filtering，使用画圆的方式进行多此查询，但这样计算量也会变大。
image.png