本章重点是motif搜索问题，19年发表一篇综述总结该类算法。

Problem 4.1两两距离

Write an algorithm that, given a set X, calculates the multiset ∆X. :::info If is a set of n points on a line segment in increasing order, then denotes the multiset of all pairwise distances between points in X: . For example, if X={0,2,4,7,10}, then ∆X={2,2,3,3,4,5,6,7,8,10}
:::

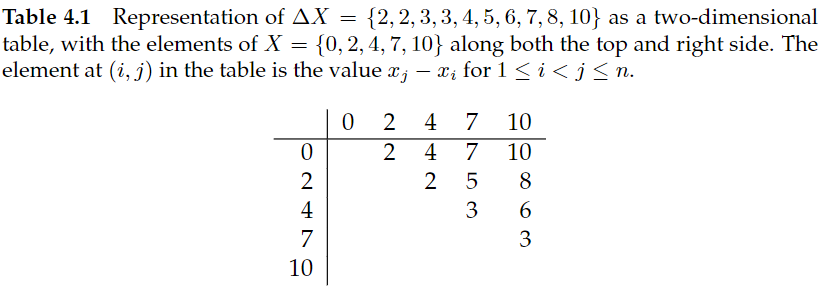from typing import List
def deltaX(X: List[int]) -> List[int]:
    return [X[j] - X[i] for i in range(len(X)) for j in range(i + 1, len(X))]
print(deltaX([1, 4, 5, 6, 8, 9]))

Problem 4.2 Partial Digest problem

Consider partial digest L = {1,1,1,2,2,3,3,3,4,4,5,5,6,6,6,9,9,10,11,12,15}.Solve the Partial Digest problem for L (i.e., find X such that ∆X = L).
对书本当中几个算法进行总结下：

1、暴力算法：

from typing import List
def bruteforcePDP(L: List[int], n: int) -> List[int]:
    """通过ΔX=L构建切割位点集合：暴力枚举长度为n的集合
    输入：L[i] >= 0且任意i > 0有L[i] >= L[i-1]
    输出：List[int]
    """
    M = max(L)
    X = [0]
    def backtrace(idx: int) -> None:
        """使用回溯法枚举集合{0,Xi,..,M},枚举所有满足该集合内两两距离与L相同的集合"""
        if idx == n - 1:
            X.append(M)
            if sorted(X[j] - X[i] for i in range(n - 1) for j in range(i + 1, n)) == L:
                print(X)
            X.pop()
            return
        for Xi in range(1, M):  # Xi ∈ [1,M]
            X.append(Xi)
            backtrace(idx + 1)
            X.pop()
    backtrace(1)
bruteforcePDP([2,2,3,3,4,5,6,7,8,10], 5)
# [0, 2, 4, 7, 10]
# [0, 3, 6, 8, 10]

复杂度分析：

• 时间复杂度：每个数字可在[1, M-1]范围中选择，一个要选择n-2个数，时间复杂度为 。
• 空间复杂度：

  2、暴力剪枝：

  Xi一定在L集合当中，当M特别大的时候这个prune（剪枝）非常有用！当输入L = {2, 998, 1000}时，此算法将比上面快很多。 ```python from typing import List

def anotherbruteforcePDP(L: List[int], n: int) -> List[int]: “””通过ΔX=L构建切割位点集合：优化枚举长度为n的集合 输入：L[i] >= 0且任意i > 0有L[i] >= L[i-1] 输出：List[int] “”” M = max(L) candidate = set(L) X = [0] def backtrace(idx: int) -> None: “””使用回溯法枚举集合{0,Xi,..,M},枚举所有满足该集合内两两距离与L相同的集合””” if idx == n - 1: X.append(M) if sorted(X[j] - X[i] for i in range(n - 1) for j in range(i + 1, n)) == L: print(X) X.pop() return for Xi in candidate: # Xi ∈ L X.append(Xi) backtrace(idx + 1) X.pop() backtrace(1)

anotherbruteforcePDP([2,2,3,3,4,5,6,7,8,10], 5)

**复杂度分析**：
- **时间复杂度**：从集合`L`中选择`n-2`个数的方案数为 ![](https://cdn.nlark.com/yuque/__latex/2c8fbb0696956c25b245bca0919970a1.svg#card=math&code=C_%7B%7CL%7C%7D%5E%7Bn-2%7D&id=DscpF)，其中集合`L`最坏情况下全为不同数字，即长度为 ![](https://cdn.nlark.com/yuque/__latex/096207826dda577a42691a52ee301ba0.svg#card=math&code=%7CL%7C%20%3D%20%5Cfrac%7Bn%28n%2B1%29%7D%7B2%7D&id=UPNzO)，因此总的时间复杂度为 ![](https://cdn.nlark.com/yuque/__latex/c04e569bca1c75d55ef1dcda01f91da8.svg#card=math&code=O%28n%5E%7B2n-4%7D%29&id=IRu0g)。
- **空间复杂度**：![](https://cdn.nlark.com/yuque/__latex/c04e569bca1c75d55ef1dcda01f91da8.svg#card=math&code=O%28n%5E%7B2n-4%7D%29&id=n5Hvz)
<a name="wg167"></a>
## 3、从最长试探性构建
由于python中没有multiset数据结构，同时也不需要复杂的集合操作，因此可以使用计数器字典数据结构替换。
```python
import typing
from collections import Counter
def delete(cnt: typing.Counter[int], element: int) -> None:
    """从计数器集合cnt中删除element元素，删除操作都是合法"""
    cnt[element] -= 1
    if 0 == cnt[element]:  # 出现次数为0则删除
        cnt.pop(element)
def place(width: int, L: typing.Counter[int], X: typing.Counter[int]) -> None:
    """每次从集合L中选出最大，分别尝试放在左侧或者右侧是否合法
    1、找到最大值width，它一定是两端点，从L中删除得到集合δ
    2、生成集合δ肯定也有最大值端点，因此选择k=max(δ)，其有两种放置可能：
        放在k-0处（右）或 width-k（左）。分别检验放入后该集合内两两之间距离是否都在集合δ中
    """
    if not L:  # 证明到达终点，找到一个合法解
        print(sorted(X.elements()))
        return
    for p in [max(L), width - max(L)]:
        removeCnt = Counter()  # 将删除操作都记录下来方便回溯时恢复原样
        for x in X:
            distance = abs(p - x)
            if distance in L:
                removeCnt[distance] += 1
                delete(L, distance)
            else:
                break
        else:  # 两两距离都在L中
            X[p] += 1  # 选择 p
            place(width, L, X)
            delete(X, p)  # 撤销 p
        L += removeCnt  # 撤销放在 p 处对L集合影响
def PartialDigest(L: typing.Counter[int], n: int) -> typing.Counter[int]:
    """从较长段开始枚举：
    输入：L[i] >= 0且任意i > 0有L[i] >= L[i-1]
    输出：List[int]
    """
    width = max(L)
    delete(L, width)
    X = Counter([0, width])
    place(width, L, X)
PartialDigest(Counter([2,2,3,3,4,5,6,7,8,10]), 5)

复杂度分析：

• 时间复杂度：，由公式，一轮需要 检验当前选择位置之一是否合法（指数级）。
• 空间复杂度：

  4、多项式算法：The chords’ problem

  The chords’ problem.pdf

  Problem 4.3 枚举长度为m的子集（不可重复）

  Write an algorithm that, given an n-element set, generates all m-element subsets of this set. For example, the set {1,2,3,4} has six two-element subsets {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, and {3,4}. How long will your algorithm take to run? Can it be done faster?
  暴力回溯：
  组合
  更好的答案可以参考下面链接：

  Problem 4.4 枚举长度为m的子集（可重复）

  Write an algorithm that, given an n-element multiset, generates allm-element subsets of this set. For example, the set {1,2,2,3} has four two-element subsets {1,2}, {1,3}, {2,3}, and {2,2}. How long will your algorithm take to run? Can it be done faster?
  出现重复原因：

1. 可重集合无序性，例如[2, 1, 2]和[1, 2, 2]相同，可以按有序枚举某个解集答案。
2. 输入集合中有重复元素，选择时要避免重复，避免重复方式有两种。

子集
代码就是将上面枚举子集长度为k = 2记录下来。

Problem 4.5 证明两集合 homeometric

Prove that the sets and are homometric for any two sets U and V. :::info In general, sets A and B are said to be homometric if 。 概念参照 Problem 4.1。
注意：书本正文写的是 是 multiset，而问题问是 set，在本题中 multiset 是 set 父集，因此我们假设是 multiset，这样解决办法对 set 也通用。 ::: 假设可重集合 ，标记 分布表示来自可重集合
集合

集合

那么对于两个 可重集合第 项，设 分布表示来自集合 ，且有 ，那么其与最后一项的距离都为 。因此同理可得之后 项到第 项距离都相同。综上可得 ，因此两集合是 homeometric。

Problem 4.6

Given a multiset of integers A = {ai}, we call the polynomial the generating function for A. Verify that the generating function for is . Given generating functions for U and V , find generating functions for and . Compare generating functions for ∆A and ∆B. Are they the same?

Problem 4.7 PARTIALDIGEST 代码实现

Write pseudocode for the PARTIALDIGEST algorithm that has fewer lines than the one presented in the text.
书本上给的伪代码：

import typing
from collections import Counter
def delete(cnt: typing.Counter[int], element: int) -> None:
    """从计数器集合cnt中删除element元素，删除操作都是合法"""
    cnt[element] -= 1
    if 0 == cnt[element]:  # 出现次数为0则删除
        cnt.pop(element)
def place(width: int, L: typing.Counter[int], X: typing.Counter[int]) -> None:
    """每次从集合L中选出最大，分别尝试放在左侧或者右侧是否合法
    1、找到最大值width，它一定是两端点，从L中删除得到集合δ
    2、生成集合δ肯定也有最大值端点，因此选择k=max(δ)，其有两种放置可能：
        放在k-0处（右）或 width-k（左）。分别检验放入后该集合内两两之间距离是否都在集合δ中
    """
    if not L:  # 证明到达终点，找到一个合法解
        print(sorted(X.elements()))
        return
    for p in [max(L), width - max(L)]:
        removeCnt = Counter()  # 将删除操作都记录下来方便回溯时恢复原样
        for x in X:
            distance = abs(p - x)
            if distance in L:
                removeCnt[distance] += 1
                delete(L, distance)
            else:
                break
        else:  # 两两距离都在L中
            X[p] += 1  # 选择 p
            place(width, L, X)
            delete(X, p)  # 撤销 p
        L += removeCnt  # 撤销放在 p 处对L集合影响
def PartialDigest(L: typing.Counter[int], n: int) -> typing.Counter[int]:
    """从较长段开始枚举：
    输入：L[i] >= 0且任意i > 0有L[i] >= L[i-1]
    输出：List[int]
    """
    width = max(L)
    delete(L, width)
    X = Counter([0, width])
    place(width, L, X)
PartialDigest(Counter([2,2,3,3,4,5,6,7,8,10]), 5)

Problem 4.8 求最短∆X：其来源X不止一个

Find a set ∆X with the smallest number of elements that could have arisen from more than one X, not counting shifts and reflections.

来自搜索引擎答案： CS431 homework 1
Page 87 of the textbook provides an example with a ∆X of size 36, so the sets from which it arises are of size 9. An example with ∆X of size 15 arises from X = {0, 1, 2, 5, 7, 9, 12} and X’ = {0, 1, 5, 7, 8, 10, 12}, where the ∆X = ∆X’ = {1, 1, 2, 2, 2, 3, 3, 4, 4, 5, 5, 5, 6, 7, 7, 7, 8, 9, 10, 11, 12}. Here |X| = |X’| = 6. Now we will consider sets of size less than 6. A ∆X with a single element x has only one solution, X = {0, x}, if we ignore its shifts and reflections. The next possible size for ∆X is 3, since the size must be of the form , and Let ∆X be {a, b, c}, where a ≤ b ≤ c. In any case, the first exit must be at distance 0 and the last exit at distance c. Therefore, for ∆X to be valid it must be true that c − b = a, and c − a = b, and the exits are also at those distances, so flipping the values of a and b result in the same output. This means that any ∆X of size 3 produces two turnpikes, each of which is the reflection of the other. Remaining possibilities for the size of ∆X is and . We are not sure if there are ∆X of size 6 or 10.