- Implement MotifEnumeration暴力">Implement MotifEnumeration暴力
- https://rosalind.info/problems/ba2a/solutions/#comment-9887">代码来源:https://rosalind.info/problems/ba2a/solutions/#comment-9887
- Implement GreedyMotifSearch">Implement GreedyMotifSearch
- Implement RandomizedMotifSearch">Implement RandomizedMotifSearch
- Implement GibbsSampler概率">Implement GibbsSampler概率
- Implement DistanceBetweenPatternAndStrings">Implement DistanceBetweenPatternAndStrings
Implement MotifEnumeration暴力
1、枚举k-mer所有可能+在允许d次错配条件下,某k-mer是否都在每条DNA中
由于引入汉明距离不超过d的条件下,k-mer串可能非某条DNA的子串。例如案例结果中ATA不是任一DNA串的子串。因此我们需要枚举长度为的k-mer串的所有可能情况,然后将每个k-mer串去检查每条DNA中是否存与该k-mer串的汉明距离≤d的子串。
from typing import Listdef hammingDistance(s: str, t: str) -> int:dist = 0for ch1, ch2 in zip(s, t):if ch1 != ch2:dist += 1return distdef MotifEnumeration(DNAs: List[str], k: int, d: int) -> List[str]:from itertools import productans = []for kmer in product('ACGT', repeat=k): # (笛卡尔乘积)所有k-mer串appearCnt = 0for dna in DNAs:# 检查当前dna串中是否存在与kmer的汉明距离≤d的子串for i in range(len(dna) - k + 1):# 可优化:不看完整串,当s[,i]与t[,i]的距离>d时直接passif hammingDistance(dna[i:i+k], kmer) <= d:appearCnt += 1break# 可优化:如果当前dna串中不存在,可以认定kmer串非答案if appearCnt == len(DNAs):ans.append("".join(kmer)) # ('A', 'T', 'A')return anss = """3 1ATTTGGCTGCCTTACGGTATCGAAAATT"""kd, *DNAs = s.splitlines()k, d = map(int, kd.split())print(*MotifEnumeration(DNAs, k, d))
复杂度分析:设总DNA串数为,每条DNA平均长度为
- 对每个DNA串的所有长度为k的子串搜索其邻居串放入集合,集合长度为
,时间复杂度为
- 对所有DNA产生的的集合取公共交集,时间复杂度不超过
```python from FrequentWordsWithMismatch import neighbours
def motifEnumeration (dna, k, d): ‘’’ Function to generate all kmers that are present in all strands of dna with at most d mismatches ‘’’
## Create an empty set for each DNA strand and fill it with all k-mers## with at most d mismatchesstrand_kmers = [set() for _ in range(len(dna))]for count,strand in enumerate(dna):for i in range(len(strand) - k + 1):kmer = strand[i:i+k]strand_kmers[count].update(neighbours(kmer,d))## Now intersect all sets to end up with only the sequences that occur## in all strandsresult = strand_kmers[0]for i in range(1,len(strand_kmers)):result.intersection_update(strand_kmers[i])return ' '.join(list(result))
代码来源:https://rosalind.info/problems/ba2a/solutions/#comment-9887
当较大时,显然此法预处理将会变得非常慢。<a name="ZGYqg"></a># [Find a Median String](https://rosalind.info/problems/ba2b/)逆向思维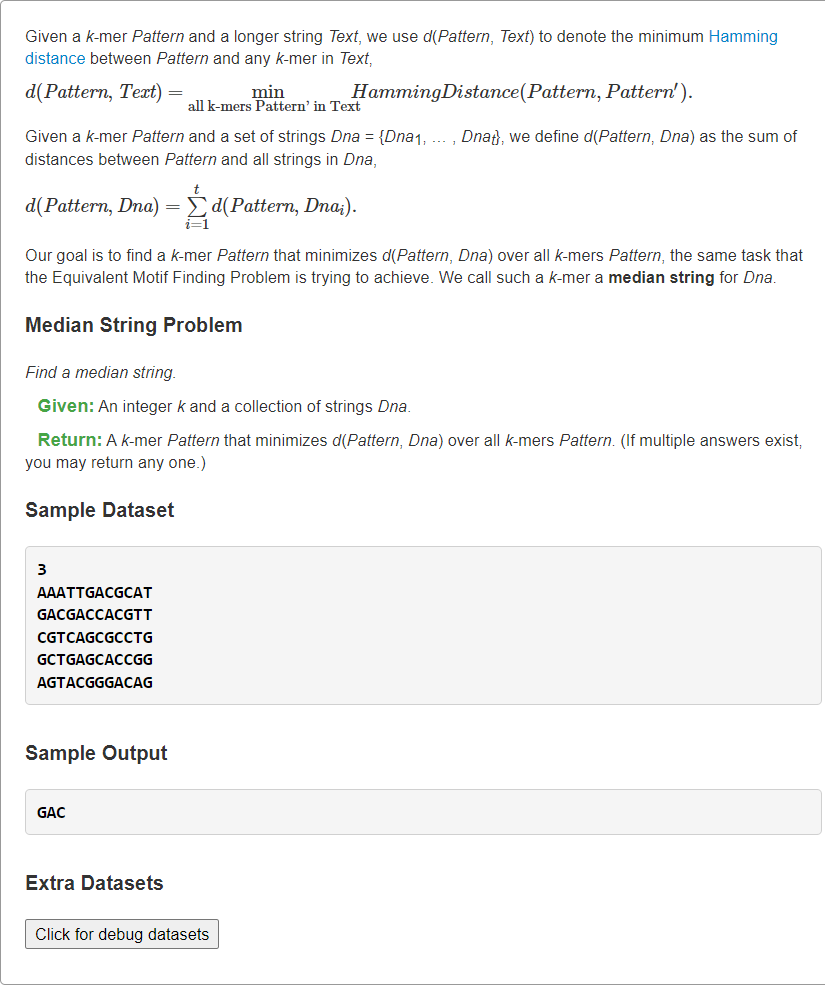<a name="JuyBj"></a>## 1、正向暴力:枚举所有Motifs→Consensus```pythonfrom typing import Listdef hammingDistance(s: str, t: str) -> int:dist = 0for ch1, ch2 in zip(s, t):if ch1 != ch2:dist += 1return distdef medianString(DNAs: List[str], k: int) -> List[str]:from itertools import product # 笛卡尔乘积from collections import Counter# 枚举每个DNA长度为k的所有子串dnaKmers = []for dna in DNAs:kmers = []for i in range(len(dna) - k + 1):kmers.append(dna[i:i+k])dnaKmers.append(kmers)# 枚举所有Motifans, ansScore = set(), float("inf")tmpConsensus = [''] * kfor motif in product(*dnaKmers): # 每个dna中选一个kmer出来构成Motif# 统计所有列小写字母(除去出现最多的字母后剩余字母)的个数# print(motif, type(motif))# motif: [kmer1, kmer2,..., kmert]score = 0for j, cols in enumerate(zip(*motif)): # cols: ('A',.., 'T',.., 'C',.., 'G')# print(cols)totCnt, maxCnt = 0, 0for base, cnt in Counter(cols).items():if maxCnt < cnt:maxCnt = cnttmpConsensus[j] = base # 更新第j列保守碱基totCnt += cntscore += totCnt - maxCnt# 更新每个motif得分最小值if ansScore >= score:if ansScore > score:ans.clear()ansScore = score# tmpConsensus必须转字符串,否则引用修改问题ans.add("".join(tmpConsensus)) # 可能重复,集合去重return list(ans)s = """3AAATTGACGCATGACGACCACGTTCGTCAGCGCCTGGCTGAGCACCGGAGTACGGGACAG"""k, *DNAs = s.splitlines()print(*medianString(DNAs, int(k)))
复杂度分析:设总DNAs串数为,每串DNA平均长度为
,pattern串长度为
- 时间复杂度:
,枚举每个DNA长度为
的所有子串的时间复杂度为
,从每条DNA序列中提取一条组成
,因此
总个数为
,对于每个
需要
时间检查。
- 空间复杂度:
,长度为
的所有pattern串可能结果。
2、逆向暴力:枚举所有Consensus→Motifs
书本上思路是逆向进行的,枚举Consensus串的所有可能,在所有串中找与DNAs的总汉明距离最小的串。 ```python from typing import List
def hammingDistance(s: str, t: str) -> int: dist = 0 for ch1, ch2 in zip(s, t): if ch1 != ch2: dist += 1 return dist
def medianString(DNAs: List[str], k: int) -> List[str]: from itertools import product # 笛卡尔乘积 ans, ansDist = [], float(“inf”) for pattern in product(‘ACGT’, repeat=k): # 所有k-mer串 totDist = 0 # d(Pattern, Dna) for dna in DNAs:
# 获得当前dna串的所有长度为k的子串与kmer串的距离的最小值 d(Pattern, Text)minDist = float("inf")for i in range(len(dna) - k + 1):minDist = min(minDist, hammingDistance(dna[i:i+k], pattern))totDist += minDist# 更新答案:题目虽只输出一条,但是我们记录所有相等答案if totDist < ansDist:ans, ansDist = [pattern], totDistelif totDist == ansDist:ans.append(pattern)return ["".join(tup) for tup in ans]
s = “””3 AAATTGACGCAT GACGACCACGTT CGTCAGCGCCTG GCTGAGCACCGG AGTACGGGACAG “”” k, DNAs = s.splitlines() print(medianString(DNAs, int(k)))
**复杂度分析**:设总DNAs串数为,每串DNA平均长度为,pattern串长度为- **时间复杂度**:,长度为的所有pattern串可能共有种,每一种查询需要进行次时间复杂度为的查询。- **空间复杂度**:,长度为的所有pattern串可能结果。<a name="HbTyy"></a># [Find a Profile-most Probable k-mer in a String](https://rosalind.info/problems/ba2c/)概率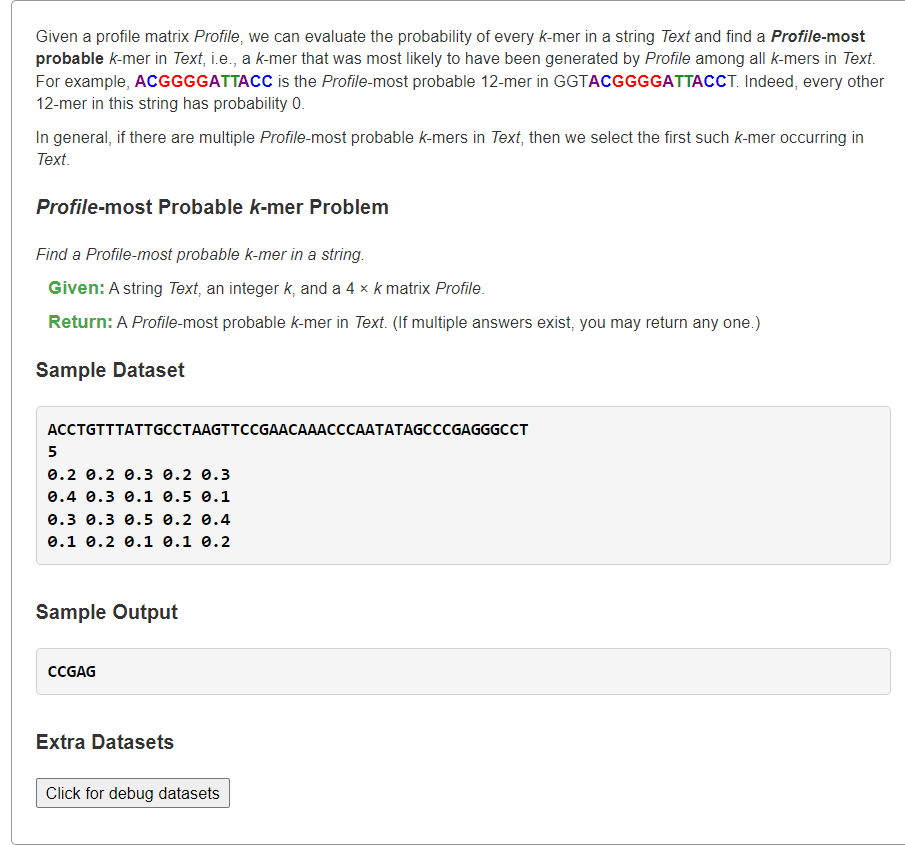<a name="YNEWM"></a>## 1、统计text所有长度为k的子串的最大概率```pythonfrom typing import Listdef profileMostProbableKmer(text: str, k: int, profile: List[List[float]]) -> List[str]:# print(text, k, profile)# 输入profile:4 * k,4行对应每列 ACGT 碱基的概率base2row = dict(zip('ACGT', range(4)))ans, ansProbable = set(), 0for i in range(len(text) - k + 1):# 计算pattern的概率pattern = text[i:i+k]pr = 1for i, base in enumerate(pattern):pr *= profile[base2row[base]][i]# 更新最大概率的答案串if ansProbable <= pr:if ansProbable < pr:ans.clear()ansProbable = prans.add("".join(pattern))return list(ans)s = """ACCTGTTTATTGCCTAAGTTCCGAACAAACCCAATATAGCCCGAGGGCCT50.2 0.2 0.3 0.2 0.30.4 0.3 0.1 0.5 0.10.3 0.3 0.5 0.2 0.40.1 0.2 0.1 0.1 0.2"""text, k, *profile = s.splitlines()profile = [[float(v) for v in line.split()] for line in profile]print(*profileMostProbableKmer(text, int(k), profile))
复杂度分析:设总text长度为,pattern串长度为
- 时间复杂度:
,text中共有
个长度为
的子串,计算每个长度为
的子串的概率为
- 空间复杂度:
,text中共有
个长度为
的子串。
Implement GreedyMotifSearch

1、已有Motif串中构建Profile,然后找当前串中Profile-most Probable的k-mer子串作为Motif
```python from typing import List
def profileMostProbableKmer(text: str, k: int, profile: List[List[float]]) -> str:
# print(text, k, profile)# 输入profile:4 * k,4行对应每列 ACGT 碱基的概率base2row = dict(zip('ACGT', range(4)))ans, ansProbable = "", -1for i in range(len(text) - k + 1):# 计算pattern的概率pattern = text[i:i+k]pr = 1for i, base in enumerate(pattern):pr *= profile[base2row[base]][i]# 更新最大概率的答案串if ansProbable < pr:ans, ansProbable = pattern, prreturn ans
def MotifsProfile(motifs: List[str]) -> List[float]: “”” Generating Profile from motifs, Profile[0][j]: the probable of A base in postion j Profile[1][j]: the probable of C base in postion j Profile[2][j]: the probable of G base in postion j Profile[3][j]: the probable of T base in postion j “”” from collections import Counter m, n = len(motifs), len(motifs[0]) base2row = dict(zip(‘ACGT’, range(4))) profile = [[0.0] n for _ in range(4)] for j, cols in enumerate(zip(motifs)): for base, cnt in Counter(cols).items(): profile[base2row[base]][j] = cnt / m return profile
def MotifsScore(motifs: List[str]) -> int: “”” SCORE(Motifs), the number of lower case letters in the motif matrix, column-by-column. “”” from collections import Counter score = 0 for cols in zip(*motifs): cnt = Counter(cols) upper_case = max(cnt, key=lambda x: cnt[x]) # 找到出现次数最多的碱基 for k, v in cnt.items(): if k != upper_case: score += v
return score
def GreedyMotifSearch(dnas: List[str], k: int, t: int) -> List[str]: n = len(dnas[0]) # 每条DNA等长 bestMotifs, bestScore = [], float(“inf”) # 得分越小越好
# 枚举第一条DNA的所有k-mer子串for i in range(n - k + 1):motifs = [dnas[0][i:i+k]]for j in range(1, t):# 从已有Motifs中生成Profileprofile = MotifsProfile(motifs)# print(motifs, profile)# 第j条DNA的Profile-most probable串作为该条DNA候选Motifmotifs.append(profileMostProbableKmer(dnas[j], k, profile))# 更新最小Motifs得分currScore = MotifsScore(motifs)if currScore < bestScore:bestMotifs, bestScore = motifs, currScore# print(bestScore)return bestMotifs
s = “””3 5 GGCGTTCAGGCA AAGAATCAGTCA CAAGGAGTTCGC CACGTCAATCAC CAATAATATTCG “”” kt, *dnas = s.splitlines()
print(GreedyMotifSearch(dnas, map(int, kt.split())), sep=”\n”)
<a name="J22gb"></a>## Explanation<a name="shUM9"></a># [Implement GreedyMotifSearch with Pseudocounts](https://rosalind.info/problems/ba2e/)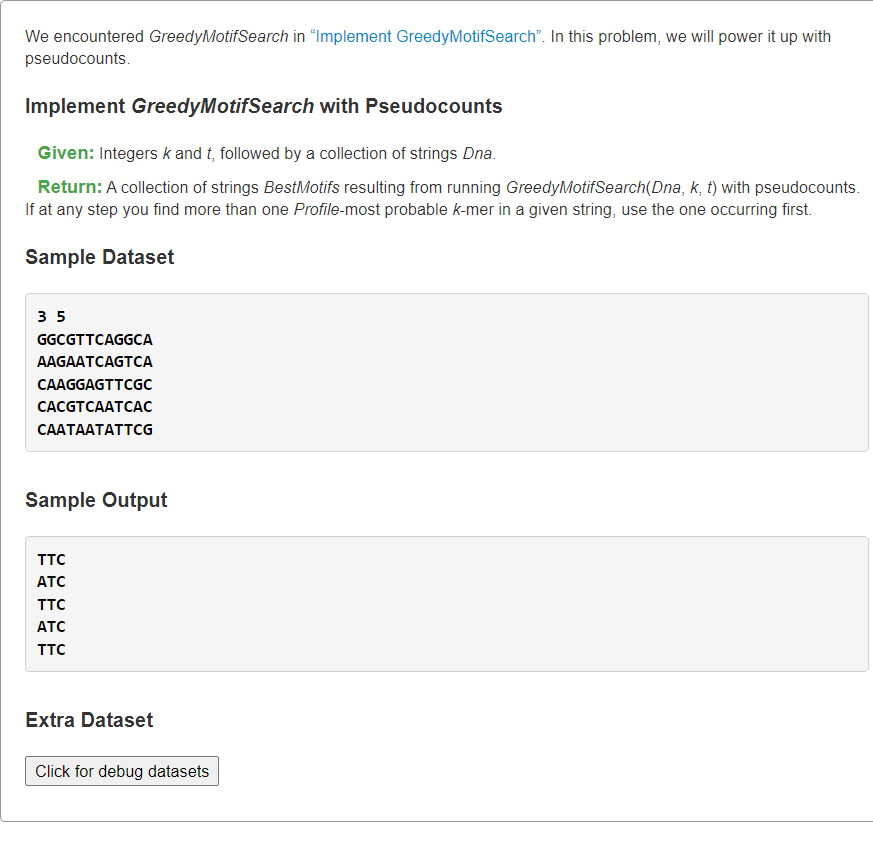<a name="VZgjk"></a>## 1、Laplace's Rule of Succession根据拉普拉斯继承法则,让概率为0的事件变为较小值事件。<br />```pythonfrom typing import Listdef profileMostProbableKmer(text: str, k: int, profile: List[List[float]]) -> str:# print(text, k, profile)# 输入profile:4 * k,4行对应每列 ACGT 碱基的概率base2row = dict(zip('ACGT', range(4)))ans, ansProbable = "", -1for i in range(len(text) - k + 1):# 计算pattern的概率pattern = text[i:i+k]pr = 1for i, base in enumerate(pattern):pr *= profile[base2row[base]][i]# 更新最大概率的答案串if ansProbable < pr:ans, ansProbable = pattern, prreturn ansdef MotifsProfile(motifs: List[str]) -> List[float]:"""Generating Profile from motifs,Profile[0][j]: the probable of A base in postion jProfile[1][j]: the probable of C base in postion jProfile[2][j]: the probable of G base in postion jProfile[3][j]: the probable of T base in postion j"""from collections import Counterm, n = len(motifs), len(motifs[0])base2row = dict(zip('ACGT', range(4)))profile = [[1 / (m + m)] * n for _ in range(4)] # Laplace's Rule of Successionfor j, cols in enumerate(zip(*motifs)):for base, cnt in Counter(cols).items():# profile[base2row[base]][j] = cnt / mprofile[base2row[base]][j] = (cnt + 1) / (m + m) # Laplace's Rule of Successionreturn profiledef MotifsScore(motifs: List[str]) -> int:"""SCORE(Motifs), the number of lower case letters in the motif matrix, column-by-column."""from collections import Counterscore = 0for cols in zip(*motifs):cnt = Counter(cols)upper_case = max(cnt, key=lambda x: cnt[x]) # 找到出现次数最多的碱基for k, v in cnt.items():if k != upper_case:score += vreturn scoredef GreedyMotifSearch(dnas: List[str], k: int, t: int) -> List[str]:n = len(dnas[0]) # 每条DNA等长bestMotifs, bestScore = [], float("inf") # 得分越小越好# 枚举第一条DNA的所有k-mer子串for i in range(n - k + 1):motifs = [dnas[0][i:i+k]]for j in range(1, t):# 从已有Motifs中生成Profileprofile = MotifsProfile(motifs)# print(motifs, profile)# 第j条DNA的Profile-most probable串作为该条DNA候选Motifmotifs.append(profileMostProbableKmer(dnas[j], k, profile))# 更新最小Motifs得分currScore = MotifsScore(motifs)if currScore < bestScore:# print(currScore, motifs)bestMotifs, bestScore = motifs, currScore# print(bestScore)return bestMotifss = """3 5GGCGTTCAGGCAAAGAATCAGTCACAAGGAGTTCGCCACGTCAATCACCAATAATATTCG"""kt, *dnas = s.splitlines()print(*GreedyMotifSearch(dnas, *map(int, kt.split())), sep="\n")
Run-ningGREEDYMOTIFSEARCHwith pseudocounts to solve the Subtle Motif Problem returns a collection of 15-mersMotifswithSCORE(Motifs)=41 andCONSENSUS(Motifs) =AAAAAtAgaGGGGtt. Thus, Laplace’s Rule of Succession has provided a great im-provement over the originalGREEDYMOTIFSEARCH, which returned the consensus stringgTtAAAtAgaGatGtGwith SCORE(Motifs)=58.
运行NingGreedyMotionSearchwith pseudocounts来解决微妙的Motif问题,返回15个mersMotifswithSCORE(Motif)=41和Consensus(Motif)=AAAAA Tagaggtt的集合。因此,拉普拉斯的继承规则大大改进了原始的GreedyMotionSearch,该搜索返回了一致的StringtTaaaTagagatgtg,分数(Motions)=58。
Implement RandomizedMotifSearch
1、1000次随机函数调用的最优解
随机函数就是书本上代码
from typing import Listfrom random import randintdef profileMostProbableKmer(text: str, k: int, profile: List[List[float]]) -> str:# print(text, k, profile)# 输入profile:4 * k,4行对应每列 ACGT 碱基的概率base2row = dict(zip('ACGT', range(4)))ans, ansProbable = "", -1for i in range(len(text) - k + 1):# 计算pattern的概率pattern = text[i:i+k]pr = 1for i, base in enumerate(pattern):pr *= profile[base2row[base]][i]# 更新最大概率的答案串if ansProbable < pr:ans, ansProbable = pattern, prreturn ansdef MotifsProfile(motifs: List[str]) -> List[float]:"""Generating Profile from motifs,Profile[0][j]: the probable of A base in postion jProfile[1][j]: the probable of C base in postion jProfile[2][j]: the probable of G base in postion jProfile[3][j]: the probable of T base in postion j"""from collections import Counterm, n = len(motifs), len(motifs[0])base2row = dict(zip('ACGT', range(4)))profile = [[1 / (m + m)] * n for _ in range(4)] # Laplace's Rule of Successionfor j, cols in enumerate(zip(*motifs)):for base, cnt in Counter(cols).items():# profile[base2row[base]][j] = cnt / mprofile[base2row[base]][j] = (cnt + 1) / (m + m) # Laplace's Rule of Successionreturn profiledef MotifsScore(motifs: List[str]) -> int:"""SCORE(Motifs), the number of lower case letters in the motif matrix, column-by-column."""from collections import Counterscore = 0for cols in zip(*motifs):cnt = Counter(cols)upper_case = max(cnt, key=lambda x: cnt[x]) # 找到出现次数最多的碱基for k, v in cnt.items():if k != upper_case:score += vreturn scoredef RandomizedMotifSearch(dnas: List[str], k: int, t: int) -> List[str]:n = len(dnas[0]) # 每条DNA等长# 随机生成第一组Motifsmotifs = []for i in range(t):beg = randint(0, n - k - 1) # [0,n-k-1]motifs.append(dnas[i][beg:beg+k]) # 该DNA的随机k-mer子串bestMotifs, bestScore = motifs, MotifsScore(motifs) # 当前Motifs当作最优解# 一直迭代找第一个“山谷”while True:# 从已有Motifs中生成Profileprofile = MotifsProfile(motifs)# 在t条DNA中找到Profile-most probable串并组成新的Motifsmotifs = [profileMostProbableKmer(dna, k, profile) for dna in dnas]# 更新最小Motifs得分currScore = MotifsScore(motifs)if currScore < bestScore:# print(currScore, motifs)bestMotifs, bestScore = motifs, currScoreelse:return bestMotifs # 书本上让证明一定存在“山谷”,即不会死循环s = """8 5CGCCCCTCTCGGGGGTGTTCAGTAAACGGCCAGGGCGAGGTATGTGTAAGTGCCAAGGTGCCAGTAGTACCGAGACCGAAAGAAGTATACAGGCGTTAGATCAAGTTTCAGGTGCACGTCGGTGAACCAATCCACCAGCTCCACGTGCAATGTTGGCCTA"""kt, *dnas = s.splitlines()# 题目要求运行RandomizedMotifSearch函数1000次,可以使用并行实现bestMotifs, bestScore = [], float("inf")for _ in range(1000):motifs = RandomizedMotifSearch(dnas, *map(int, kt.split()))currScore = MotifsScore(motifs)if currScore < bestScore:# print(currScore, motifs)bestMotifs, bestScore = motifs, currScoreprint(*bestMotifs, sep="\n")
Implement GibbsSampler概率
1、吉布斯生成器【不等概率】
Actually there is no real problem. The GibbsSampler can only find a local optimum, then stabilises there after 100 - 200 runs. So you simply have to run the GibbsSampler multiple times to find the best scoring one of the local optima. It looks like you do this for 20 runs. I guess that is a little low. You run 20 2000 times. So 200 200 should bring better results within the same time.
from typing import Listfrom random import randint, uniformdef profileRandomKmer(text: str, k: int, profile: List[List[float]]) -> str:# 输入profile:4 * k,4行对应每列 ACGT 碱基的概率# 生成非均匀分布(p1,p2,..,pk),根据几何概型得到每个kmer出现概率# 将所有概率同时除去C=sum(p)得到均匀分布:(p1/C,p2/C,..,pk/C)# 现在随机生成0~1内的数,看它落在均匀分布的哪个区间,即第几条kmerbase2row = dict(zip('ACGT', range(4)))ans, ansProbable = "", -1probabilities = []for i in range(len(text) - k + 1):# 计算pattern的概率(由于存在浮点数,无法使用滑窗优化)probability = 1.0for j in range(k):probability *= profile[base2row[text[i+j]]][j]probabilities.append(probability)# 随机生成0~1的浮点数,判断其落在(p1/C,p2/C,..,pk/C)均匀分布的哪个位置,即第几条kmerx = uniform(0, sum(probabilities))currP = 0for i, p in enumerate(probabilities):if currP + p >= x: # currP+p/C >= xreturn text[i:i+k]currP += pdef MotifsProfile(motifs: List[str]) -> List[float]:"""Generating Profile from motifs,Profile[0][j]: the probable of A base in postion jProfile[1][j]: the probable of C base in postion jProfile[2][j]: the probable of G base in postion jProfile[3][j]: the probable of T base in postion j"""from collections import Counterm, n = len(motifs), len(motifs[0])base2row = dict(zip('ACGT', range(4)))profile = [[1 / (m + m)] * n for _ in range(4)] # Laplace's Rule of Successionfor j, cols in enumerate(zip(*motifs)):for base, cnt in Counter(cols).items():# profile[base2row[base]][j] = cnt / mprofile[base2row[base]][j] = (cnt + 1) / (m + m) # Laplace's Rule of Successionreturn profiledef MotifsScore(motifs: List[str]) -> int:"""SCORE(Motifs), the number of lower case letters in the motif matrix, column-by-column."""from collections import Counterscore = 0for cols in zip(*motifs):cnt = Counter(cols)upper_case = max(cnt, key=lambda x: cnt[x]) # 找到出现次数最多的碱基for k, v in cnt.items():if k != upper_case:score += vreturn scoredef GibbsSampler(dnas: List[str], k: int, t: int, N: int) -> List[str]:n = len(dnas[0]) # 每条DNA等长# 随机生成第一组Motifsmotifs = []for i in range(t):beg = randint(0, n - k - 1) # [0,n-k-1]motifs.append(dnas[i][beg:beg+k]) # 该DNA的随机k-mer子串bestMotifs, bestScore = motifs, MotifsScore(motifs) # 当前Motifs当作最优解# 进行N轮吉布斯抽样for _ in range(N):i = randint(0, t - 1)motifs.pop(i) # 删除第i条序列profile = MotifsProfile(motifs) # 更具另外t-1条生成Profilemotifs.insert(i, profileRandomKmer(dnas[i], k, profile))currScore = MotifsScore(motifs)if currScore < bestScore:bestMotifs, bestScore = motifs, currScorereturn bestMotifss = """8 5 100CGCCCCTCTCGGGGGTGTTCAGTAAACGGCCAGGGCGAGGTATGTGTAAGTGCCAAGGTGCCAGTAGTACCGAGACCGAAAGAAGTATACAGGCGTTAGATCAAGTTTCAGGTGCACGTCGGTGAACCAATCCACCAGCTCCACGTGCAATGTTGGCCTA"""ktN, *dnas = s.splitlines()# 题目要求运行GibbsSampler函数20次,可以使用并行实现bestMotifs, bestScore = [], float("inf")for _ in range(50): # 但是20次对于案例依旧可能输出其它较大解motifs = GibbsSampler(dnas, *map(int, ktN.split()))currScore = MotifsScore(motifs)if currScore < bestScore:# print(currScore, motifs)bestMotifs, bestScore = motifs, currScoreprint(bestScore, *bestMotifs, sep="\n")
Explanation
Implement DistanceBetweenPatternAndStrings
1、模拟
from typing import Listdef hammingDistance(s: str, t: str) -> int:dist = 0for ch1, ch2 in zip(s, t):if ch1 != ch2:dist += 1return distdef DistanceBetweenPatternAndStrings(pattern: str, dnas: List[str]):k = len(pattern)totDist = 0for dna in dnas:minDist = float("inf")for i in range(len(dna) - k + 1):dist = hammingDistance(dna[i:i+k], pattern)if dist < minDist:minDist = disttotDist += minDistreturn totDists = """AAATTACCTTAAC GATATCTGTC ACGGCGTTCG CCCTAAAGAG CGTCAGAGGT"""pattern, dnas = s.splitlines()print(DistanceBetweenPatternAndStrings(pattern, dnas.split()), sep="\n")






