Generate the k-mer Composition of a String

1、所有k-mer子串排序

from typing import List
def StringComposition(k: int, text: str) -> List[str]:
    kmers = []
    for i in range(len(text) - k + 1):
        kmers.append(text[i:i+k])
    kmers.sort()
    return kmers
    # return sorted(text[i:i+k] for i in range(len(text) - k + 1))
s = """5
CAATCCAAC
"""
k, text = s.splitlines()
print(*StringComposition(int(k), text), sep="\n")

复杂度分析：设 text 长度为 n

• 时间复杂度：，共生成条长度为的子串，排序消耗
• 空间复杂度：

  2、后缀数组

Reconstruct a String from its Genome Path

1、遍历图

from typing import List
def StringSpelled2GenomePath(patterns: List[str]) -> str:
    genome = patterns[0]
    for i in range(1, len(patterns)):
        genome += patterns[i][-1]
    return genome
s = """ACCGA
CCGAA
CGAAG
GAAGC
AAGCT
"""
patterns = s.splitlines()
print(StringSpelled2GenomePath(patterns), sep="\n")

Construct the Overlap Graph of a Collection of k-mers

1、O(n^2)建有向图

本题所要求的两点之间有一条有向边的条件是。但是现在不清楚两个节点之间关系，因此我们需要枚举所有对，最暴力方式是双层循环 最后需要注意答案是以邻接表实现，也就是最终答案是以有向图的起点升序。

from typing import List, Tuple
def OverlapGraph(patterns: List[str]) -> List[Tuple[str]]:
    graph = []
    n = len(patterns)
    for i in range(n):
        for j in range(i + 1, n):
            u, v = patterns[i], patterns[j]
            # u -> v
            if u[1:] == v[:-1]:
                graph.append((u, v))
            # v -> u
            if v[1:] == u[:-1]:
                graph.append((v, u))
    # adjacency list
    graph.sort()
    return graph
s = """ATGCG
GCATG
CATGC
AGGCA
GGCAT
"""
patterns = s.splitlines()
for u, v in OverlapGraph(patterns):
    print(f"{u} -> {v}")

复杂度分析：设 patterns 长度为 n，graph 长度为 n^2

• 时间复杂度：，对 n^2 个元素排序。
• 空间复杂度：，邻接表

  Construct the De Bruijn Graph of a String

  

  1、从Text串获取k-mer串建De Bruijn图

  ```python from typing import List, Tuple from collections import defaultdict

def deBruijnGraph(k: int, text: str) -> List[Tuple[str, List[str]]]: graph = defaultdict(list) # 边个数不变，因此list

# 取k-mer前k-1个字符作节点，边是相邻k-mer的overlap
for i in range(len(text) - k + 1):  # 最后一个k-mer只有 k-1 个
    graph[text[i:i+k-1]].append(text[i+1:i+k])
# adjacency list
return [(node, sorted(graph[node])) for node in sorted(graph)]

s = “””4 AAGATTCTCTAC””” k, text = s.splitlines() for u, v in deBruijnGraph(int(k), text): print(f”{u} -> {‘,’.join(v)}”)

<a name="dUgyG"></a>
# [Construct the De Bruijn Graph of a Collection of k-mers](https://rosalind.info/problems/ba3e/)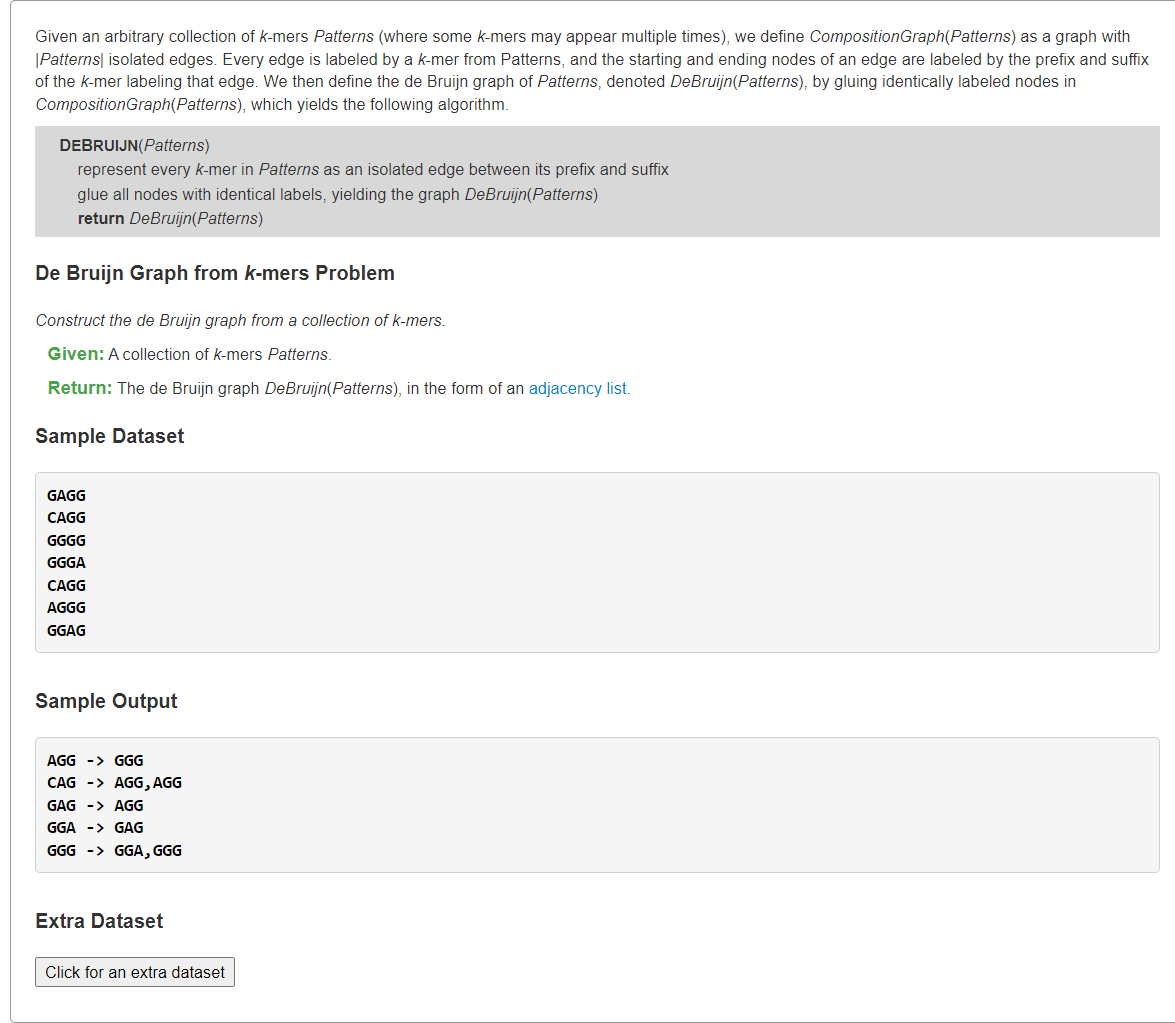
![rosalind.info_problems_ba3e_.png](https://cdn.nlark.com/yuque/0/2022/png/1438957/1656247597474-dcbe91f4-4148-4786-8b88-01e7db3072de.png#clientId=u488605a0-ad03-4&crop=0&crop=0&crop=1&crop=1&from=drop&id=ub5e3f1c3&margin=%5Bobject%20Object%5D&name=rosalind.info_problems_ba3e_.png&originHeight=1023&originWidth=1175&originalType=binary&ratio=1&rotation=0&showTitle=false&size=85418&status=done&style=none&taskId=u9f0a0831-3e17-4c70-afd3-3d64315a20f&title=)
<a name="AWCoN"></a>
## 1、从k-mers中建De Bruijn图
由于输入都是某文本串`text`的所有`k-mer`子串，他们顺序是乱的，但是现在要从它们之中构建出De Bruijn图<br />节点：所有串的前缀和后缀构成的无重复集合。<br />边：长度为`k`的子串`s`的前缀`s[0,n-2]`和后缀`s[1,n-1]`之间构成一条边。
![](https://cdn.nlark.com/yuque/__graphviz/7f147fc888fc36b07ab34541844300f1.svg#lake_card_v2=eyJ0eXBlIjoiZ3JhcGh2aXoiLCJjb2RlIjoiZGlncmFwaCB7XG5cdHJhbmtkaXI9TFJcblx0bm9kZSBbc2hhcGU9Y2lyY2xlXVxuXHRBR0cgLT4gR0dHXG5cdENBRyAtPiB7QUdHLEFHR31cblx0R0FHIC0-IEFHR1xuXHRHR0EgLT4gR0FHXG5cdEdHRyAtPiB7R0dBLEdHR31cbn0iLCJ1cmwiOiJodHRwczovL2Nkbi5ubGFyay5jb20veXVxdWUvX19ncmFwaHZpei83ZjE0N2ZjODg4ZmMzNmIwN2FiMzQ1NDE4NDQzMDBmMS5zdmciLCJpZCI6IkdxUUhmIiwibWFyZ2luIjp7InRvcCI6dHJ1ZSwiYm90dG9tIjp0cnVlfSwiY2FyZCI6ImRpYWdyYW0ifQ==)```python
from typing import List, Tuple
from collections import defaultdict
def deBruijnGraphFromKmers(patterns: List[str]) -> List[Tuple[str, List[str]]]:
    graph = defaultdict(list)
    for pattern in patterns:
        graph[pattern[:-1]].append(pattern[1:])
    # adjacency list
    return [(node, sorted(graph[node])) for node in sorted(graph)]
s = """GAGG
CAGG
GGGG
GGGA
CAGG
AGGG
GGAG"""
patterns = s.splitlines()
for u, v in deBruijnGraphFromKmers(patterns):
    print(f"{u} -> {','.join(v)}")

Find an Eulerian Cycle in a Graph

6->8->7->9->6->5->4->2->1->0->3->2->6