Compute the Number of Times a Pattern Appears in a Textoverlap

1、暴力：O(|t||p|)

如题干的算法伪代码所示：

def patternCount(text: str, pattern: str) -> int:
    """Count overlapping substring in a given string"""
    m, n = len(text), len(pattern)
    count = 0
    for i in range(0, m - n + 1):
        if text[i:i+n] == pattern:
            count += 1
    return count
s = """GCGCG
GCG
"""
print(patternCount(*s.splitlines()))

pub fn count_pattern(text: &str, pattern: &str) -> u32 {
  let mut count = 0;
  let num = pattern.len();
  let length = text.len();
  // println!("Length: {}/{}", length, num);
  for (idx, _) in text.chars().enumerate() {
    let max_len = idx + num;
    if max_len < length {
      match &text[idx..(idx + num)] == pattern {
        true => count = count + 1,
        _ => continue,
      }
    }
  }
  return count;
}

2、strstr

28. 实现 strStr()

public class KMP {
public static void main(String[] args) {
    int[] ababas = kmp ("ab");
    System.out.println (Arrays.toString (ababas));
    int i = kmpSearch ("abababababa", "aba", ababas);
    System.out.println (i);
}
public static int[] kmp(String s){ //AAADAAAADDA
    int[] temp = new int[s.length ()];
    temp[0] = 0;
    for (int i = 0,j=1; j < s.length (); j++) {
        while (i>0&&s.charAt (i)!=s.charAt (j)){
            i = temp[i-1];
        }
        if (s.charAt (i)==s.charAt (j)) {
            i++;
        }
        temp[j] = i;
    }
    return temp;
}
public static int kmpSearch(String str1,String str2,int[] next){
    //遍历str1
    int ans = 0;
    for (int i = 0,j = 0; i < str1.length (); i++) {
        while (j>0&&str1.charAt (i)!=str2.charAt (j)){
            j = next[j-1];
        }
        if (str1.charAt (i)==str2.charAt (j)){
            j++;
        }
        if (j==str2.length ()&&j>=2){
            ans++;
            j = next[j-2];
            i--;
        }
    }
    return ans;
}
}
作者：Condescending ColdenjK1
链接：https://leetcode.cn/circle/discuss/Cqoohu/view/FHApDf/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

3、SA+Height

后缀数组+height数组，将t#s连起来后得后缀数组，排序获得height，然后找s出现位置。

Find the Most Frequent Words in a Stringoverlap

1、暴力：O(|t|2|k|)

枚举中所有长度为的子串作为，然后调用计算该串重叠出现次数。注意：由于中所有长度为的子串可能有重复，因此若它们出现次数都是最大，最终输出要去重。实现上就是用集合记录最频繁出现的

from typing import List
def patternCount(text: str, pattern: str) -> int:
    """Count overlapping substring in a given string"""
    m, n = len(text), len(pattern)
    count = 0
    for i in range(0, m - n + 1):
        if text[i:i+n] == pattern:
            count += 1
    return count
def mostFrequentWord(text: str, k: int) -> List[str]:
    """Find the Most Frequent Words in a String"""
    ans, cnt = {}, 0  # pattern may be repeat, so we use set to deduplicate.
    for i in range(len(text) - k + 1):
        # enumerate all k-mer substring
        pattern = text[i:i+k]
        count = patternCount(text, pattern)
        if cnt < count:
            ans = {pattern}
            cnt = count
        elif cnt == count:
            ans.add(pattern)
    return list(ans)
s = """ACGTTGCATGTCGCATGATGCATGAGAGCT
4
"""
text, k = s.splitlines()
print(*mostFrequentWord(text, int(k)))

dna <- ("ACGTTGCATGTCGCATGATGCATGAGAGCT")
n <- 4
kmer.list <- numeric(nchar(dna)-(n-1))
for (i in 1:(nchar(dna)-(n-1))){
  kmer.list[i] <- substring(dna, i, (i+(n-1)))
}
kmer.list <- as.matrix(subset(kmer.list, kmer.list > 0))
kmer.list <- as.matrix(sort(table(kmer.list), decreasing = TRUE))
frequent_words <- function(text, k) {
  frequentpatterns <- matrix()
  textunlisted <- unlist(strsplit(text, split=""))
  n <- nchar(text)
  for (i in 1:(n-k+1)) {
    pattern <- paste(textunlisted[i:(i+k-1)], collapse="")
    count[[i]] <- matrix(pattern_count(text,pattern))
  }
  maxcount <- max(count)
  for (i in 1:(n-k+1)){
    if(count[[i]] == maxcount)
      frequentpatterns[[i]] <- matrix(paste(textunlisted[i:(i+k-1)], collapse=""))
  }
  frequentpatterns <- unique(frequentpatterns)
  frequentpatterns <- frequentpatterns[!is.na(frequentpatterns)]
  return(frequentpatterns)
}

2、k长度滑窗+滚动哈希+计数器：O(|t|+|k|)

from typing import List
from collections import Counter
def mostFrequentWord(text: str, k: int) -> List[str]:
    """Find the Most Frequent Words in a String"""
    cnt = Counter(text[i:i+k] for i in range(len(text) - k + 1))
    maxCnt = max(cnt.values())
    return [s for s, v in cnt.items() if v == maxCnt]
s = """ACGTTGCATGTCGCATGATGCATGAGAGCT
4
"""
text, k = s.splitlines()
print(*mostFrequentWord(text, int(k)))

哈希表可以通过 排序+双指针 实现计数

3、SA

Explanation

Find the Reverse Complement of a String

1、模拟

def reverseComplementOfDNA(dna: str) -> str:
    """Find the Reverse Complement of a String"""
    # return dna.translate(str.maketrans('AGCT', 'TCGA'))[::-1]
    d = dict(zip('AGCT', 'TCGA'))
    n = len(dna)
    ret = [''] * n
    for i in range(n):
        ret[n-1-i] = d[dna[i]]
    return "".join(ret)
print(reverseComplementOfDNA("AAAACCCGGT"))

Explanation

Find All Occurrences of a Pattern in a Stringoverlap

1、KMP找出所有匹配位置

28. 实现 strStr()

from typing import List
def strstr(t: str, p: str) -> List[int]:
    """Find all the occurence place of p in t"""
    m, n = len(t), len(p)
    if n == 0:
        return [0]
    # calculate next array
    next = [0] * n
    i, j = 1, 0
    while i < n:
        while j > 0 and p[i] != p[j]:
            j = next[j-1]
        if p[i] == p[j]:
            j += 1
        next[i] = j
        i += 1
    # print(next)
    # KMP
    idxs = []
    i, j = 0, 0
    while i < m:
        while j > 0 and t[i] != p[j]:
            j = next[j-1]
        if t[i] == p[j]:
            j += 1
        if j == n:
            # we can return i - n + 1 if find the first occurence place, 
            # otherwise assume t[i] != p[n-1]
            idxs.append(i - n + 1)
            j = next[n-1]  
        i += 1
    # print(idxs)
    return idxs
s = """ATAT
GATATATGCATATACTT
"""
p, t = s.splitlines()
print(*strstr(t, p))

fn main() {
    let pattern = "ATAT";
    let genome = String::from("GATATATGCATATACTT");
    let positions = find_pattern_positions(pattern, genome) ;
    for pos in positions {
        print!("{} ",pos)
    }
}
fn find_pattern_positions(pattern: &str, genome:String) -> Vec<u32> {
    let mut positions: Vec<u32> = Vec::new();
    for i in 0..genome.len()-pattern.len(){
        if genome[i..i+pattern.len()] == *pattern {
            positions.push(i as u32);
        }
    } 
    positions
}

Find Patterns Forming Clumps in a String

1、暴力：O(L2k|Genome|)

def FrequencyTable(text, k):
    freq_map = {}
    n = len(text)
    for i in range(0, n - k + 1):
        pattern = text[i:i + k]
        if pattern not in freq_map:
            freq_map[pattern] = 1
        else:
            freq_map[pattern] = freq_map[pattern] + 1
    return freq_map
def FindClumps(text, k, l, t):
    patterns = set()
    n = len(text)
    for i in range(n - l + 1):
        window = text[i:i + l]
        freq_map = FrequencyTable(window, k)
        for s in freq_map:
            if freq_map[s] >= t:
                patterns.add(s)
    return ' '.join(patterns)
filename = 'rosalind_ba1e.txt'
file = open(filename, 'r')
lines = file.readlines()
text = lines[0].strip()
params = lines[1].strip().split()
k, l, t = [int(p) for p in params]
print(FindClumps(text, k, l, t))

2、所有k-mer出现位置+第i个出现位置到第i+t个出现位置的距离是否≤L

区间段覆盖问题

from typing import List
def clumpFind(genome: str, k: int, L: int, t: int) -> List[str]:
    # O(nk): enumerate k-mer in genome
    n = len(genome)
    kmerIdxs = {}  # {k-mer: indexs}
    for i in range(n - k + 1):
        p = genome[i:i+k]  # can be optimize with rolling hash
        # add the occurrence of p in Genome
        kmerIdxs.setdefault(p, []).append(i)
    ans = []
    # 时间复杂度较难计算，但<<O(n^2) 
    # 对每个k-mer出现位置，看L长度内有多少个（滑窗O(|idx|)解决）
    # if the number overlap occurence idx >= t
    for s, idx in kmerIdxs.items():
        left = 0
        for right in range(len(idx)):
            # slide in idx[right]
            # check the length of idx[left]~idx[right]
            while left <= right and idx[right] - idx[left] + 1 > L:
                left += 1
            if right - left + 1 >= t:
                ans.append(s)
                break
    return ans
s = """CGGACTCGACAGATGTGAAGAAATGTGAAGACTGAGTGAAGAGAAGAGGAAACACGACACGACATTGCGACATAATGTACGAATGTAATGTGCCTATGGC
5 75 4
"""
lines = s.splitlines()
genome = lines[0]
k, L, t = map(int, lines[1].split())
print(*clumpFind(genome, k, L, t))

3、评论区最优解法：长度为L的滑窗（初始化+滑入/出一个k-mer）

本题可以overlap，左侧滑出，那么起点为的 k-mer 数少一，滑入，那么起点为的 k-mer 数加一，窗口内的所有起点的 k-mer 数不变，因此每次滑动只需要判断新进来的起点为的 k-mer 数是否 ≥ t
总时间复杂度为

• 初始化滑窗：枚举长度为窗口内所有长度为的子串需要，可用滚动哈希优化为
• 每次滑动转移需要计算滑入/出的k-mer串的哈希值，时间复杂度为 :::info 进阶：非overlap
  30. 串联所有单词的子串，时间复杂度为O(k×|G|k) :::

  Explanation

  

  Find a Position in a Genome Minimizing the Skew

  

  1、G,C目前累计数量->G-C差值

  ```python from typing import List

def minimumSkew(dna: str) -> List[int]: n = len(dna) minv, ans = n, [] G = C = 0 for i in range(n): if dna[i] == ‘G’: G += 1 elif dna[i] == ‘C’: C += 1 if G - C < minv: ans = [i + 1] # next place is oriC minv = G - C elif G - C == minv: ans.append(i + 1) # next place is oriC return ans

s = “””CCTATCGGTGGATTAGCATGTCCCTGTACGTTTCGCCGCGAACTAGTTCACACGGCTTGATGGCAAATGGTTTTTCCGGCGACCGTAATCGTCCACCGAG”””

print(*minimumSkew(s))

<a name="CkIoo"></a>
# [Compute the Hamming Distance Between Two Strings](https://rosalind.info/problems/ba1g/)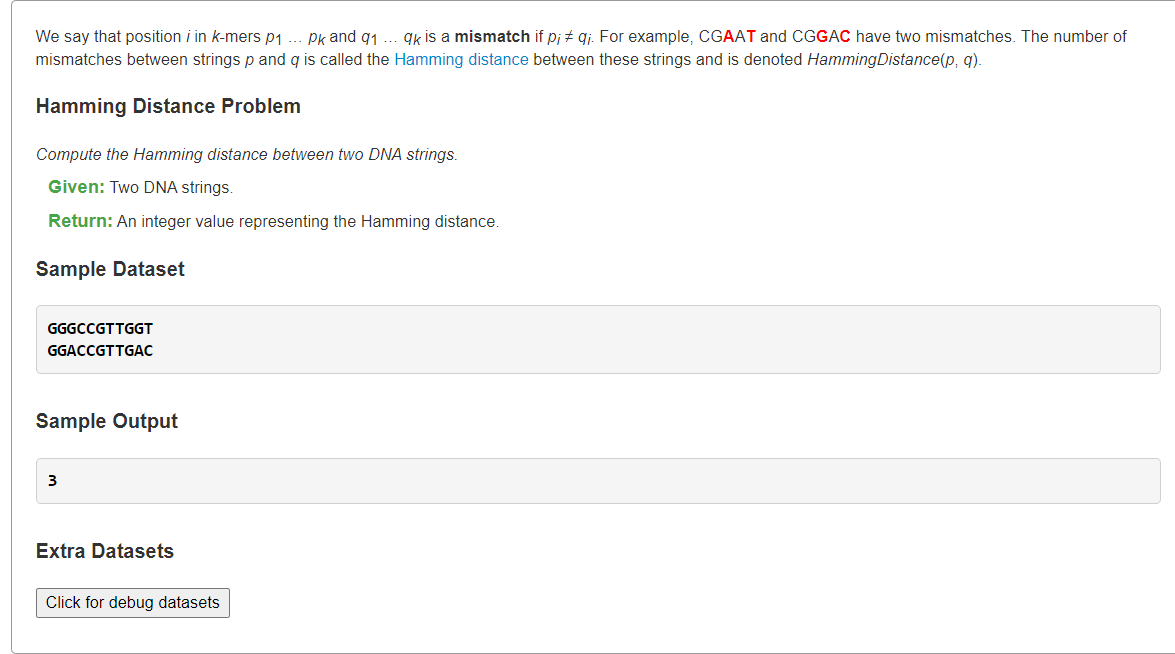
![rosalind.info_problems_ba1g_.png](https://cdn.nlark.com/yuque/0/2022/png/1438957/1652190714036-2612c61f-beab-4f84-8a24-73b2cf68978f.png#clientId=u4f4af40e-e31d-4&crop=0&crop=0&crop=1&crop=1&from=drop&id=ubc71f5fb&margin=%5Bobject%20Object%5D&name=rosalind.info_problems_ba1g_.png&originHeight=654&originWidth=1175&originalType=binary&ratio=1&rotation=0&showTitle=false&size=46271&status=done&style=shadow&taskId=u0dd8af46-763b-46fc-88b4-459e8dbab90&title=)
<a name="YcT8P"></a>
## 1、汉明距离：统计每位s[i]!=t[i]总数
```python
def hammingDistance(s: str, t: str) -> int:
    dist = 0
    for ch1, ch2 in zip(s, t):
        if ch1 != ch2:
            dist += 1
    return dist
s = """GGGCCGTTGGT
GGACCGTTGAC"""
s, t = s.splitlines()
print(hammingDistance(s, t))

Find All Approximate Occurrences of a Pattern in a String

1、暴力解：O(|T||P|)

枚举text中所有长度为的子串， 检验其与的汉明距离是否小于等于d，是就将索引加入答案。

from typing import List
def hammingDistance(s: str, t: str) -> int:
    dist = 0
    for ch1, ch2 in zip(s, t):
        if ch1 != ch2:
            dist += 1
    return dist
def approximatePatternMatch(text: str, pattern: str, d: int) -> List[int]:
    m, n = len(text), len(pattern)
    ans = []
    for i in range(m - n + 1):
        if hammingDistance(text[i:i+n], pattern) <= d:
            ans.append(i)
    return ans
s = """ATTCTGGA
CGCCCGAATCCAGAACGCATTCCCATATTTCGGGACCACTGGCCTCCACGGTACGGACGTCAATCAAATGCCTAGCGGCTTGTGGTTTCTCCTACGCTCC
3
"""
pattern, text, d = s.splitlines()
print(*approximatePatternMatch(text, pattern, int(d)))

2、待更新DP

允许错配
https://en.wikipedia.org/wiki/Approximate_string_matching
https://www.cs.unc.edu/~prins/Classes/555/Media/Lec18.pdf
测试用例：
https://bioinformaticsalgorithms.com/data/debugdatasets/replication/ApproximatePatternMatchingProblem.pdf

Generate the d-Neighborhood of a StringBFS/DFS

1、枚举所有长度为|Pattern|的组成可能+汉明距离筛选

最直观的方式就是生成个所有可能序列，然后在它们中筛出与的汉明距离≤d的构成答案。

def get_d_neighbors(pattern: str, d: int) -> str:
    return "\n".join(
        [
            x
            for x in (
                "".join(i)
                for i in itertools.product(["A", "T", "G", "C"], repeat=len(pattern))
            )
            if hamming_distance(pattern, x) <= d
        ]
    )

复杂度分析：

• 时间复杂度：，一次汉明距离筛选需要，总共进行次

• 空间复杂度：

  2、记录枚举树中所有节点

  :::info 书本上代码允许一个位置突变多次，且允许突变为自身，因此可能出现s[i]->...->s[i]，导致产生很多重复集，最终结果需要使用集合去重。
  如果我们限制最多突变一次且只能突变为非字符，就能保证每次突变产生不同结果。 ::: 如下图s = ACG, d = 2的枚举树，层序号就是与s的汉明距离，例如第1层表示其与s距离为1。其中淡蓝色的节点是重复出现，去重方式就是保证突变位置递增，因此所求答案就是所有非重复树节点。
  
  复杂度分析：设长度为，字符集，汉明距离差为

• 时间复杂度：，分别枚举突变次数从，第次突变可发生在个位置之一，该次突变结果有种（不允许变成自己），第次突变可发生在个位置之一（不允许一个位置突变多次），该次突变结果有种（不允许变成自己），因此突变数为时，产生种结果。

• 空间复杂度：

  实现1：DFS/回溯

  评论区的DFS算法，其去重方式要求每次修改位置必须是递增，因此其枚举树就是上图 ```python def Neighbors(Pattern, k, d, start = 0): neighbors = [Pattern] # 初始化把自己加入 if d > 0:

    for i in range(start, k):
        for symbol in "ACGT":
            if symbol != Pattern[i]:
                new_pattern = Pattern[:i] + symbol + Pattern[i+1:]
                new_neighbors = Neighbors(new_pattern, k, d - 1, i + 1)  # 注意i+1
                neighbors.extend(new_neighbors)

  return neighbors

kmer = input() d = int(input()) neighbors = Neighbors(kmer, len(kmer), d) for neighbor in neighbors: print(neighbor)

01选取：对于每个位置![](https://cdn.nlark.com/yuque/__latex/b355b418b4897ebe9ef04778df03a3b1.svg#card=math&code=s%5Bi%5D&id=d9BD3)有两种选择，突变或不突变：
- 不突变：那么总突变数![](https://cdn.nlark.com/yuque/__latex/56c1b0cb7a48ccf9520b0adb3c8cb2e8.svg#card=math&code=d&id=TRDqr)不变，继续向后求解![](https://cdn.nlark.com/yuque/__latex/5195e3a1c22eddbccb14d553c0c35622.svg#card=math&code=s%5Bi%2B1%2C%5D&id=dk8OT)中总突变数为![](https://cdn.nlark.com/yuque/__latex/56c1b0cb7a48ccf9520b0adb3c8cb2e8.svg#card=math&code=d&id=e2fF6)的结果
- 突变：前提是![](https://cdn.nlark.com/yuque/__latex/c9e1e0c625406b78101eb07fd0d7c453.svg#card=math&code=d%5Cgt%200&id=x7GJk)，当前突变结果有三种（下面代码规定![](https://cdn.nlark.com/yuque/__latex/b355b418b4897ebe9ef04778df03a3b1.svg#card=math&code=s%5Bi%5D&id=xezfv)只允许一次有效突变：![](https://cdn.nlark.com/yuque/__latex/b355b418b4897ebe9ef04778df03a3b1.svg#card=math&code=s%5Bi%5D&id=dyf50)不能突变两次或突变一次变回![](https://cdn.nlark.com/yuque/__latex/b355b418b4897ebe9ef04778df03a3b1.svg#card=math&code=s%5Bi%5D&id=JTMsC)），每种使用回溯选择一下，继续向后求解![](https://cdn.nlark.com/yuque/__latex/5195e3a1c22eddbccb14d553c0c35622.svg#card=math&code=s%5Bi%2B1%2C%5D&id=ixVcZ)中总突变数为![](https://cdn.nlark.com/yuque/__latex/e6ecc3ef1343a9b617b11e1dcb6470c5.svg#card=math&code=d-1&id=agpIO)的结果
```python
from typing import List
def neighbors(pattern: str, d: int) -> List[str]:
    s = list(pattern)  # 转数组可修改
    ans = []  # 回溯生成不重复，每个s[i]只能变为字符集内其它字符
    def backtrace(idx: int, d: int) -> None:  # 去重一：保证idx递增
        # 递归出口
        if idx >= len(s) or d == 0:
            ans.append("".join(s))
            return
        # 当前选择不变
        backtrace(idx + 1, d)
        # 当前选择突变
        if d > 0:
            orginBase = s[idx]
            for base in "ACGT":
                if base != orginBase:  # 去重二：保证s[i]变为其它字符
                    s[idx] = base  # 选择
                    backtrace(idx + 1, d - 1)
            s[idx] = orginBase  # 撤销
    backtrace(0, d)
    # print(len(ans) == len(set(ans)))
    return ans
s = """ACG
1
"""
s, d = s.splitlines()
print(*neighbors(s, int(d)), sep='\n')

实现2：BFS【从src向下搜d层】

从上往下一层层搜索，但是怎么去重呢？

def mutation(s, d):
    ans = set()
    queue = []
    dist = {}
    queue.append(s)
    # 此dist字典没必要，其就是记录BFS层数，使用layer变量记录即可
    dist[s] = 0  # d[t]表示s->...->t共花费几步（允许同位置变多次+变为自己）
    ans.add(s)  # 使用集合去重
    while len(queue) != 0:
        cur = queue.pop(0)   # 可以改为collections.deque
        for i in range(len(cur)):
            cur_l = list(cur)
            for j in bp:  # 允许s[i]→s[i]，因此会产生重复解
                cur_l[i] = j
                new_str = "".join(cur_l)
                #print(new_str)
                # 使用ans标记重复，防止重复节点搜索，也就是s[i]只能变为非s[i]字符
                if new_str not in ans and dist[cur] + 1 <= d:
                    ans.add(new_str)
                    queue.append(new_str)
                    dist[new_str] = dist[cur] + 1
        return ans

上面代码使用来标记访问过的节点，这样可以保证不重复，即最终所求答案，但是dist字典根本没用
我们可以使用每层突变位置必须是递增的方式来去重，也就是节点设计为(src, mutPos)，下一个节点突变位置只能在mutPos + 1 -> |src|-1。

from typing import List
def neighbors(pattern: str, d: int) -> List[str]:
    ans = [pattern]  # d=0将自己加入
    from collections import deque
    q = deque([(pattern, -1)])
    while d:
        for _ in range(len(q)):
            u, mutPos = q.popleft()
            # 突变位置递增且s[i]只能变为字符集内其它字符可保证生成结果不重复
            for i in range(mutPos + 1, len(u)):
                for base in "ACGT":
                    if u[i] != base:
                        v = u[:i] + base + u[i+1:]
                        ans.append(v)  # 记录入队节点
                        q.append((v, i))
        # print("next layer: ", q)
        d -= 1
    # print(len(ans) == len(set(ans)))
    return ans
s = """ACG
2
"""
s, d = s.splitlines()
print(*neighbors(s, int(d)), sep='\n')

Explanation

书本上的代码是允许多次突变+允许突变回，这样就会出现大量重复解，因此需要用集合去重。

Implement PatternToNumber字符串转对应四进制数

1、分支界定法：x是字典序第几（从0开始计数）

AGT排第几？前缀AG位于第二层且序号为2，即左侧有2个兄弟节点，它们每个可向下生长N=4个分支，因此AG的第一个孩子序号为2 * N，而T是AG的第4个字典序孩子，因此其序号为2 * N + 3
AGTG排第几？前缀AGT位于第三层且序号在为11，即左侧有11个兄弟节点，它们每个可向下生长N=4个分支，因此共AGT的的第一个孩子序号为11 * N，而G是AGT的第3个字典序孩子，因此其序号为11 * N + 2

综上有公式：
当前串的序号 = prefix的序号 分支个数N + 当前字符ch的字典序
那么prefix串的序号怎么求呢？其可以继续带入上面公式，因此这个是递归问题。
递归函数定义：返回串在由字符集构成的字典序顺序（从0开始计数）
递归出口：当时，直接看该字符在排第几返回；实际也可将时返回当作出口，因为其不影响结果。
递归链条：若，拆分除前缀和末尾字符，当前的序号 = 序号 分支个数N + 当前字符的字典序

symbol2index = dict(zip('ACGT', range(4)))
def pattern2number(pattern: str) -> int:
    if not pattern:
        return 0
    number = symbol2index[pattern[-1]]
    return 4 * pattern2number(pattern[:-1]) + number

2、N进制

上面方法本质上就是四进制计数，因为一共有4个类型，因此可以用0, 1, 2, 3分别表示碱基A, C, G, T。例如我们枚举0-15序号的串

2位比特可以表示0-3范围的数，因此如上所示数字越小就表示其字典序越小

symbol2index = dict(zip('ACGT', range(4)))
def pattern2number(pattern: str) -> int:
    digit = 0
    for ch in pattern:
        digit = digit * 4 + symbol2index[ch]
    return digit
print(pattern2number("AGTG"))

Implement NumberToPattern四进制数转对应字符串

1、从四进制数恢复字符串

上面字符串转四进制数的逆过程，我们可以对四进制数不断%4得最低位的权值，将此权值”翻译”回对应字符，然后不断重复将其/4获得次低位的权值，直到四进制数变为零。 :::info 注意：
题目给定四进制数index和最终字符串长度k的目的是防止index=0时，上述算法就会以为结束，输出位数可能不对。 :::

def number2pattern(index: int, k: int) -> str:
    # 递归出口
    if k == 0:
        return ""
    # 递归链条
    prefixIndex, index = divmod(index, 4)
    return number2pattern(prefixIndex, k - 1) + index2symbol[index]
print(number2pattern(45, 4))

def number2pattern(index: int, k: int) -> str:
    ret = [''] * k
    while k > 0:
        index, r = divmod(index, 4)
        ret[k-1] = index2symbol[r]  # 逆序填充
        k -= 1
    return "".join(ret)
print(number2pattern(45, 4))

Find the Most Frequent Words with Mismatches in a String4^k个k-mer频数表

1、开足4k哈希桶(枚举所有k-mer串可能情况)

from typing import List
symbol2int = dict(zip('ACGT', range(4)))
def pattern2number(pattern: str) -> int:
    if not pattern:
        return 0
    number = symbol2int[pattern[-1]]
    return 4 * pattern2number(pattern[:-1]) + number
def computingFrequencyArray(text: str, k: int) -> List[int]:
    table = [0] * (4 ** k)
    for i in range(len(text) - k + 1):
        table[pattern2number(text[i:i+k])] += 1  # 转为4进制，hasher
    return table
s = """ACGCGGCTCTGAAA
2
"""
lines = s.splitlines()
text = lines[0]
k = int(lines[1])
print(*computingFrequencyArray(text, k))

:::info 只是本题要求所有k-mer在Text串中的频数表，这样耗费空间。 :::

Find the Most Frequent Words with Mismatches in a String4^k个k-mer汉明距离≤d

1、枚举4k个k-mer并用暴力双指针匹配

from typing import List
def hammingDistance(s: str, t: str) -> int:
    dist = 0
    for ch1, ch2 in zip(s, t):
        if ch1 != ch2:
            dist += 1
    return dist
def approximatePatternMatch(text: str, pattern: str, d: int) -> List[int]:
    m, n = len(text), len(pattern)
    ans = []
    for i in range(m - n + 1):
        if hammingDistance(text[i:i+n], pattern) <= d:
            ans.append(i)
    return ans
def frequentWordswithMismatches(text: str, k: int, d: int) -> List[str]:
    def backtrace(n: int, path: List[str], ans: List[str]) -> None:
        if n == 0:
            ans.append("".join(path))
            return
        for base in 'AGCT':
            path.append(base)
            backtrace(n - 1, path, ans)
            path.pop()
    kmers = []
    backtrace(k, [], kmers)
    # print(kmers)
    ans, maxv = [], 0
    for pattern in kmers:
        cnt = len(approximatePatternMatch(text, pattern, d))
        if cnt > maxv:
            ans = [pattern]
            maxv = cnt
        elif cnt == maxv:
            ans.append(pattern)
    return ans
s = """ACGTTGCATGTCGCATGATGCATGAGAGCT
4 1
"""
lines = s.splitlines()
text = lines[0]
k, d= map(int, lines[1].split()) 
print(*frequentWordswithMismatches(text, k, d))

并行计算：

Find Frequent Words with Mismatches and Reverse Complements