支持向量机 - 软间隔与正则化 - 《机器学习笔记》

求解软间隔支持向量机
支持向量机和逻辑回归的联系与区别
正则化

上一节中，通过利用核函数映射来解决非线性可分的问题，但现实中很难找到合适的核函数，即使某个核函数能令训练集在新特征空间中线性可分，也难保这不是过拟合造成的结果。

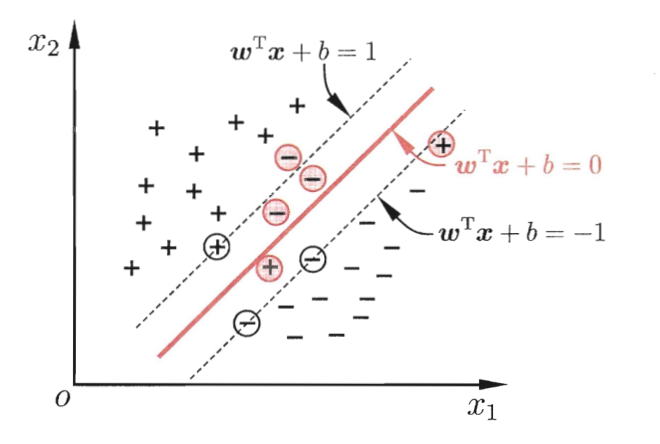
比方说上面这张图，红线是此时的划分超平面，最大间隔很小。但事实上，红色色圆圈圈起的点是一个 outlier，可能是噪声的原因，它偏离了正确的分布。而训练模型时，我们并没有考虑这一点，这就导致把训练样本中的 outlier当成数据的真实分布拟合了，也即过拟合。

但当我们允许这个 outlier 被误分类时，得到的划分超平面可能就如图中深红色线所示，此时的最大间隔更大，预测新样本时误分类的概率也会降低很多。

在实际任务中，outlier 的情况可能更加严重。我们甚至会无法构造出一个能将数据划分开的超平面。

缓解该问题的一个思路就是允许支持向量机在一些样本上出错，为此，引入软间隔（soft margin）的概念。软间隔是相对于硬间隔（hard margin）的一个概念，硬间隔要求所有样本都必须划分正确，也即约束：

$软间隔与正则化 - 图2$ %20%5Cgeq%201%0A#card=math&code=y_i%28%5Cmathbf%7Bw%7D%5ET%5Cmathbf%7Bx%7D_i%2Bb%29%20%5Cgeq%201%0A&id=V5aPe)

软间隔则允许某些样本不满足约束（根据约束条件的不同，有可能某些样本出现在间隔内，甚至被误分类）。此时目标函数可以重写为：

$软间隔与正则化 - 图3$ -1)%20%5Cqquad%20(12)%0A#card=math&code=%5Cmin%7B%5Cmathbf%7Bw%7D%2Cb%7D%20%5Cfrac%7B1%7D%7B2%7D%20%5CVert%20%5Cmathbf%7Bw%7D%20%5CVert%5E2%20%2B%20C%20%5Csum%7Bi%3D1%7D%5Em%20%5Cell_%7B0%2F1%7D%28y_i%28%5Cmathbf%7Bw%7D%5ET%5Cmathbf%7Bx%7D%2Bb%29-1%29%20%5Cqquad%20%2812%29%0A&id=nmINK)

其中 $软间隔与正则化 - 图4$ 是0/1损失函数：

$软间隔与正则化 - 图5$ %3D%0A%5Cleft%0A%5C%7B%5Cbegin%7Barray%7D%0A%5C%5C1%2C%20%5Cquad%20if%5C%20z%3C0%3B%0A%5C%5C0%2C%20%5Cquad%20otherwise.%0A%5Cend%7Barray%7D%0A%5Cright.#card=math&code=%5Cell_%7B0%2F1%7D%28z%29%3D%0A%5Cleft%0A%5C%7B%5Cbegin%7Barray%7D%0A%5C%5C1%2C%20%5Cquad%20if%5C%20z%3C0%3B%0A%5C%5C0%2C%20%5Cquad%20otherwise.%0A%5Cend%7Barray%7D%0A%5Cright.&id=Ys5gA)

它的含义很简单：如果分类正确，那么函数间隔必定大于等于1，此时损失为0；如果分类错误，那么函数间隔必定小于等于-1，此时损失为1。

而 $软间隔与正则化 - 图6$ 则是一个大于0的常数，当 $软间隔与正则化 - 图7$ 趋于无穷大时，式（12）等效于带约束的式（1），因为此时对误分类的惩罚无限大，也即要求全部样本分类正确。当 $软间隔与正则化 - 图8$ 取有限值时，允许某些样本分类错误。

由于0/1损失函数是一个非凸不连续函数，所以式（12）难以求解，于是在实际任务中，我们采用一些凸的连续函数来取替它，这样的函数就称为替代损失（surrogate loss）函数。

最常用的有以下三种：

hinge损失： $软间隔与正则化 - 图9$ %20%3D%20%5Cmax%20(0%2C1-z)#card=math&code=%5Cell_%7Bhinge%7D%28z%29%20%3D%20%5Cmax%20%280%2C1-z%29&id=QG7db)
指数损失（exponential loss）： $软间隔与正则化 - 图10$ %20%3D%20%5Cexp%20(-z)#card=math&code=%5Cell_%7B%5Cexp%7D%28z%29%20%3D%20%5Cexp%20%28-z%29&id=l3DeK)
对率损失（logistic loss）： $软间隔与正则化 - 图11$ %20%3D%20%5Clog%20(1%2B%5Cexp%20(-z)%20)#card=math&code=%5Cell_%7B%5Clog%7D%28z%29%20%3D%20%5Clog%20%281%2B%5Cexp%20%28-z%29%20%29&id=WeQCG)

不妨作图观察比较一下这些损失函数：

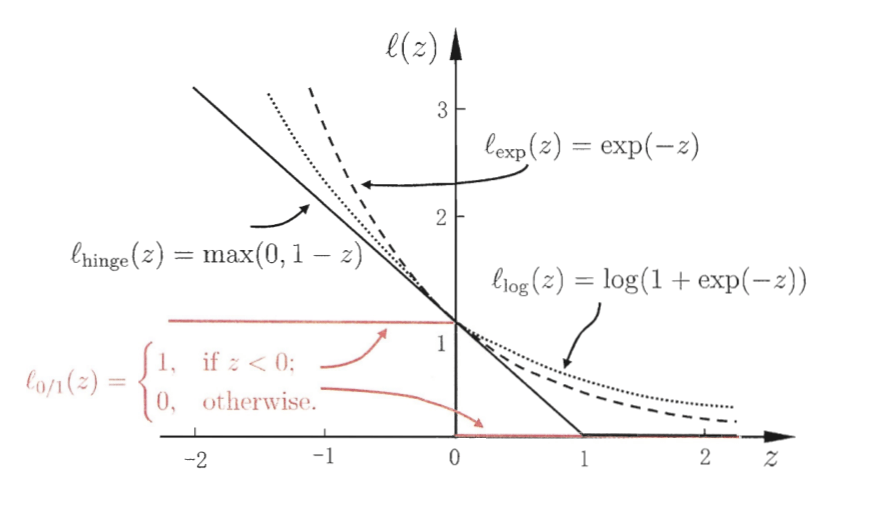
这里有个问题是，书中提到对率损失中 $软间隔与正则化 - 图13$ 指 $软间隔与正则化 - 图14$ ，也即底数为自然对数，但这种情况下对率损失在 $软间隔与正则化 - 图15$ 处不为1，而是0.693。但是书中的插图里，对率损失经过 $软间隔与正则化 - 图16$ #card=math&code=%280%2C1%29&id=x9PKC) 点，此时底数应为2，上面的插图就是按底数为2计算的。

实际任务中最常用的是hinge损失，这里就以hinge损失为例，替代0/1损失函数，此时目标函数式（12）可以重写为：

$软间隔与正则化 - 图17$ )%20%5Cqquad%20(13)%0A#card=math&code=%5Cmin%7B%5Cmathbf%7Bw%7D%2Cb%7D%20%5Cfrac%7B1%7D%7B2%7D%20%5CVert%20%5Cmathbf%7Bw%7D%20%5CVert%5E2%20%2B%20C%20%5Csum%7Bi%3D1%7D%5Em%20%5Cmax%280%2C%201-y_i%28%5Cmathbf%7Bw%7D%5ET%5Cmathbf%7Bx%7D%2Bb%29%29%20%5Cqquad%20%2813%29%0A&id=fX1fH)

引入松弛变量（slack variables） $软间隔与正则化 - 图18$ ，可以把式（13）重写为：

$软间隔与正则化 - 图19$ %20%5Cgeq%201-%5Cxii%2C%20%5Cquad%20%5Cxi_i%20%5Cgeq%200%2C%20%5Cquad%20i%3D1%2C2%2C…%2Cm%20%5Cqquad%20(14)%0A#card=math&code=%5Cmin%7B%5Cmathbf%7Bw%7D%2Cb%7D%20%5Cfrac%7B1%7D%7B2%7D%20%5CVert%20%5Cmathbf%7Bw%7D%20%5CVert%5E2%20%2B%20C%20%5Csum_%7Bi%3D1%7D%5Em%20%5Cxi_i%20%5Cquad%20s.t.%20%5Cquad%20y_i%28%5Cmathbf%7Bw%7D%5ET%5Cmathbf%7Bx%7D%2Bb%29%20%5Cgeq%201-%5Cxi_i%2C%20%5Cquad%20%5Cxi_i%20%5Cgeq%200%2C%20%5Cquad%20i%3D1%2C2%2C…%2Cm%20%5Cqquad%20%2814%29%0A&id=cDzhO)

该式描述的就是软间隔支持向量机，其中每个样本都对应着一个松弛变量，用以表示该样本误分类的程度，松弛变量的值越大，程度越高。

求解软间隔支持向量机

式（14）仍然是一个二次规划问题，类似于前面的做法，分以下几步：

通过拉格朗日乘子法把 $软间隔与正则化 - 图20$ 个约束转换 $软间隔与正则化 - 图21$ 个拉格朗日乘子，得到该问题的拉格朗日函数。
分别对 $软间隔与正则化 - 图22$ 求偏导，代入拉格朗日函数得到对偶问题。
使用SMO算法求解对偶问题，解出所有样本对应的拉格朗日乘子。
需要进行新样本预测时，使用支持向量及其对应的拉格朗日乘子进行求解。

特别地，因为式（14）有两组各 $软间隔与正则化 - 图23$ 个不等式约束，所以该问题的拉格朗日函数有 $软间隔与正则化 - 图24$ 和 $软间隔与正则化 - 图25$ 两组拉格朗日乘子。特别地，对松弛变量 $软间隔与正则化 - 图26$ 求导，令导数为0会得到一条约束式：

$软间隔与正则化 - 图27$ %0A#card=math&code=C%20%3D%20a_i%20%2B%20%5Cmu_i%20%5Cqquad%20%2815%29%0A&id=MN48v)

有意思的是，软间隔支持向量机的对偶问题和硬间隔几乎没有不同，只是约束条件修改了一下：

$软间隔与正则化 - 图28$ %0A#card=math&code=%5Cmax%7B%5Cmathbf%7Ba%7D%7D%20%5Csum%7Bi%3D1%7D%5Em%20ai%20-%20%5Cfrac%7B1%7D%7B2%7D%20%5Csum%7Bi%3D1%7D%5Em%5Csum%7Bj%3D1%7D%5Em%20a_i%20a_j%20y_i%20y_j%20%5Cmathbf%7Bx%7D_i%5ET%20%5Cmathbf%7Bx%7D_j%20%5Cquad%20s.t.%20%5Cquad%20%5Csum%7Bi%3D1%7D%5Em%20a_i%20y_i%20%3D%200%2C%20%5Cquad%200%20%5Cleq%20a_i%20%5Cleq%20C%2C%20%5Cquad%20i%3D1%2C2%2C…%2Cm%20%5Cqquad%20%2816%29%0A&id=NjtBJ)

这里的 $软间隔与正则化 - 图29$ 不仅要求大于等于0，还要求小于等于 $软间隔与正则化 - 图30$ 。

类似地，由于式（14）的约束条件是不等式约束，所以求解过程要求满足KKT（Karush-Kuhn-Tucker）条件：

$软间隔与正则化 - 图31$ -1%2B%5Cxi_i%20%5Cgeq%200%3B%0A%5C%5Ca_i%20(y_i%20f(%5Cmathbf%7Bx%7D_i)-1%2B%5Cxi_i)%20%3D%200%3B%0A%5C%5C%5Cxi_i%20%5Cgeq%200%3B%0A%5C%5C%5Cmu_i%5Cxi_i%20%3D%200.%0A%5Cend%7Barray%7D%0A%5Cright.#card=math&code=%5Cleft%0A%5C%7B%5Cbegin%7Barray%7D%0A%5C%5Ca_i%20%5Cgeq%200%3B%0A%5C%5C%5Cmu_i%20%5Cgeq%200%3B%0A%5C%5Cy_i%20f%28%5Cmathbf%7Bx%7D_i%29-1%2B%5Cxi_i%20%5Cgeq%200%3B%0A%5C%5Ca_i%20%28y_i%20f%28%5Cmathbf%7Bx%7D_i%29-1%2B%5Cxi_i%29%20%3D%200%3B%0A%5C%5C%5Cxi_i%20%5Cgeq%200%3B%0A%5C%5C%5Cmu_i%5Cxi_i%20%3D%200.%0A%5Cend%7Barray%7D%0A%5Cright.&id=LXvzf)

KKT条件可以理解为下面几点：

对任意训练样本，
- 要么对应的拉格朗日乘子 $软间隔与正则化 - 图32$ ；
- 要么函数间隔等于1和对应的松弛变量之差（ $软间隔与正则化 - 图33$ %20%3D%201-%5Cxi_i#card=math&code=y_i%28%5Cmathbf%7Bw%7D%5ET%5Cmathbf%7Bx%7D%2Bb%29%20%3D%201-%5Cxi_i&id=sWiyp)）。

如果一个样本的拉格朗日乘子 $软间隔与正则化 - 图34$ ，则它对模型没有任何影响，不需要保留。
如果一个样本的拉格朗日乘子大于0，则它是支持向量。
- 如果拉格朗日乘子 $软间隔与正则化 - 图35$ 小于 $软间隔与正则化 - 图36$ ，按照式（15）有 $软间隔与正则化 - 图37$ ，
  因此松弛变量 $软间隔与正则化 - 图38$ ，此时函数间隔为1，样本落在最大间隔边界上。
- 如果拉格朗日乘子等于，按照式（15）有，因此松弛变量。
  - 若 $软间隔与正则化 - 图43$ ，则样本落在间隔内，但依然被正确分类。
  - 若 $软间隔与正则化 - 图44$ ，则样本落在另一个类的间隔外，被错误分类

上图就展示了一个典型的软间隔支持向量机。图中就有一些异常点，这些点有的虽然在虚线与超平面之间（ $软间隔与正则化 - 图46$ %20%3C%201#card=math&code=0%20%3C%20y_i%28%5Cmathbf%7Bw%7D%5ET%5Cmathbf%7Bx%7D%2Bb%29%20%3C%201&id=AcdFE)），但也能被正确分类（比如 $软间隔与正则化 - 图47$ ）。有的点落到了超平面的另一侧，就会被误分类（比如 $软间隔与正则化 - 图48$ h和 $软间隔与正则化 - 图49$ ）。

特别地，在 R. Collobert. 的论文 Large Scale Machine Learning 中提到，常数 $软间隔与正则化 - 图50$ 一般取训练集大小的倒数（ $软间隔与正则化 - 图51$ ）。

支持向量机和逻辑回归的联系与区别

上面用的是hinge损失，不过我们也提到了还有其他一些替代损失函数，事实上，使用对率损失时，SVM得到的模型和LR是非常类似的。

支持向量机和逻辑回归的相同点：

都是线性分类器，模型求解出一个划分超平面；
两种方法都可以增加不同的正则化项；
通常来说性能相当。

支持向量机和逻辑回归的不同点：

LR使用对率损失，SVM一般用hinge损失；
在LR的模型求解过程中，每个训练样本都对划分超平面有影响，影响力随着与超平面的距离增大而减小，所以说LR的解受训练数据本身的分布影响；SVM的模型只与占训练数据少部分的支持向量有关，所以说，SVM不直接依赖数据分布，所得的划分超平面不受某一类点的影响；
如果数据类别不平衡比较严重，LR需要先做相应处理再训练，SVM则不用；
SVM依赖于数据表达的距离测度，需要先把数据标准化，LR则不用（但实际任务中可能会为了方便选择优化过程的初始值而进行标准化）。如果数据的距离测度不明确（特别是高维数据），那么最大间隔可能就变得没有意义；
LR的输出有概率意义，SVM的输出则没有；
LR可以直接用于多分类任务，SVM则需要进行扩展（但更常用one-vs-rest）；
LR使用的对率损失是光滑的单调递减函数，无法导出支持向量，解依赖于所有样本，因此预测开销较大；SVM使用的hinge损失有“零区域”，因此解具有稀疏性（书中没有具体说明这句话的意思，但按我的理解是解出的拉格朗日乘子 $软间隔与正则化 - 图52$ 具有稀疏性，而不是权重向量 $软间隔与正则化 - 图53$ ），从而不需用到所有训练样本。

在实际运用中，LR更常用于大规模数据集，速度较快；SVM适用于规模小，维度高的数据集。

在 Andrew NG 的课里讲到过：

如果Feature的数量很大，跟样本数量差不多，这时候选用LR或者是Linear Kernel的SVM；
如果Feature的数量比较小，样本数量一般，不算大也不算小，选用SVM+Gaussian Kernel；
如果Feature的数量比较小，而样本数量很多，需要手工添加一些feature变成第一种情况。

正则化

事实上，无论使用何种损失函数，SVM的目标函数都可以描述为以下形式：

$软间隔与正则化 - 图54$ %20%2B%20C%20%5Csum%7Bi%3D1%7D%5Em%20%5Cell(f(%5Cmathbf%7Bx%7D_i)%2C%20y_i)%20%5Cqquad%20(17)%0A#card=math&code=%5Cmin_f%20%5COmega%28f%29%20%2B%20C%20%5Csum%7Bi%3D1%7D%5Em%20%5Cell%28f%28%5Cmathbf%7Bx%7D_i%29%2C%20y_i%29%20%5Cqquad%20%2817%29%0A&id=uPrpE)

在SVM中第一项用于描述划分超平面的“间隔”的大小，第二项用于描述在训练集上的误差。

更一般地，第一项称为结构风险（structural risk），用来描述模型的性质。第二项称为经验风险（empirical risk），用来描述模型与训练数据的契合程度。参数 $软间隔与正则化 - 图55$ 用于权衡这两种风险。

前面学习的模型大多都是在最小化经验风险的基础上，再考虑结构风险（避免过拟合）。SVM却是从最小化结构风险来展开的。

从最小化经验风险的角度来看， $软间隔与正则化 - 图56$ #card=math&code=%5COmega%28f%29&id=q0DlD) 表述了我们希望得到具有何种性质的模型（例如复杂度较小的模型），为引入领域知识和用户意图提供了路径（比方说贝叶斯估计中的先验概率）。

另一方面， $软间隔与正则化 - 图57$ #card=math&code=%5COmega%28f%29&id=cjPJq) 还可以帮我们削减假设空间，从而降低模型过拟合的风险。从这个角度来看，可以称 $软间隔与正则化 - 图58$ #card=math&code=%5COmega%28f%29&id=f9wPD) 为正则化（regularization）项， $软间隔与正则化 - 图59$ 为正则化常数。正则化可以看作一种罚函数法，即对不希望出现的结果施以惩罚，从而使优化过程趋向于期望的目标。

$软间隔与正则化 - 图60$ 范数是常用的正则化项，其中 $软间隔与正则化 - 图61$ 范数 $软间隔与正则化 - 图62$ 倾向于 $软间隔与正则化 - 图63$ 的分量取值尽量稠密，即非零分量个数尽量多； $软间隔与正则化 - 图64$ 范数 $软间隔与正则化 - 图65$ 和 $软间隔与正则化 - 图66$ 范数 $软间隔与正则化 - 图67$ 则倾向于 $软间隔与正则化 - 图68$ 的分量取值尽量稀疏，即非零分量个数尽量少。