原型聚类

K-Means

K-Means的思想十分简单，首先随机指定类中心，根据样本与类中心的远近划分类簇，接着重新计算类中心，迭代直至收敛。但是其中迭代的过程并不是主观地想象得出，事实上，若将样本的类别看做为“隐变量”（latent variable），类中心看作样本的分布参数，这一过程正是通过EM算法的两步走策略而计算出，其根本的目的是为了最小化平方误差函数E：

K-Means的算法流程如下所示：

学习向量量化（LVQ）

LVQ也是基于原型的聚类算法，与K-Means不同的是，LVQ使用样本真实类标记辅助聚类，首先LVQ根据样本的类标记，从各类中分别随机选出一个样本作为该类簇的原型，从而组成了一个原型特征向量组，接着从样本集中随机挑选一个样本，计算其与原型向量组中每个向量的距离，并选取距离最小的原型向量所在的类簇作为它的划分结果，再与真实类标比较。

若划分结果正确，则对应原型向量向这个样本靠近一些 若划分结果不正确，则对应原型向量向这个样本远离一些 .

LVQ算法的流程如下所示：

高斯混合聚类

现在可以看出K-Means与LVQ都试图以类中心作为原型指导聚类，高斯混合聚类则采用高斯分布来描述原型。现假设每个类簇中的样本都服从一个多维高斯分布，那么空间中的样本可以看作由k个多维高斯分布混合而成。

对于多维高斯分布，其概率密度函数如下所示：

%20%3D%20%5Cfrac%7B1%7D%7B(2%5Cpi)%5E%7B%5Cfrac%7Bn%7D%7B2%7D%7D%7C%5Csum%7C%5E%7B%5Cfrac%7B1%7D%7B2%7D%7D%7De%5E%7B-%5Cfrac%7B1%7D%7B2%7D(x-%5Cmu)%5ET%5Csum%5E%7B-1%7D(x-%5Cmu)%7D%20%0A#card=math&code=p%28%5Cpmb%7Bx%7D%29%20%3D%20%5Cfrac%7B1%7D%7B%282%5Cpi%29%5E%7B%5Cfrac%7Bn%7D%7B2%7D%7D%7C%5Csum%7C%5E%7B%5Cfrac%7B1%7D%7B2%7D%7D%7De%5E%7B-%5Cfrac%7B1%7D%7B2%7D%28x-%5Cmu%29%5ET%5Csum%5E%7B-1%7D%28x-%5Cmu%29%7D%20%0A&id=KFSby)

其中u表示均值向量，∑表示协方差矩阵，可以看出一个多维高斯分布完全由这两个参数所确定。接着定义高斯混合分布为：

%20%3D%20%5Csum%7Bi%3D1%7D%5Ek%20%5Calpha_i%20%5Ccdot%20p(%5Cpmb%7Bx%7D%7C%5Cpmb%7B%5Cmu%7D_i%2C%5Csum%20i)%20%20%20%20%0A#card=math&code=p%5Cmathcal%7BM%7D%28%5Cpmb%7Bx%7D%29%20%3D%20%5Csum_%7Bi%3D1%7D%5Ek%20%5Calpha_i%20%5Ccdot%20p%28%5Cpmb%7Bx%7D%7C%5Cpmb%7B%5Cmu%7D_i%2C%5Csum%20i%29%20%20%20%20%0A&id=C6Aht)

α称为混合系数，这样空间中样本的采集过程则可以抽象为：（1）先选择一个类簇（高斯分布），（2）再根据对应高斯分布的密度函数进行采样，这时候贝叶斯公式又能大展身手了：

此时只需要选择PM最大时的类簇并将该样本划分到其中，看到这里很容易发现：这和那个传说中的贝叶斯分类不是神似吗，都是通过贝叶斯公式展开，然后计算类先验概率和类条件概率。但遗憾的是：这里没有真实类标信息，对于类条件概率，并不能像贝叶斯分类那样通过最大似然法美好地计算出来，因为这里的样本可能属于所有的类簇，这里的似然函数变为：

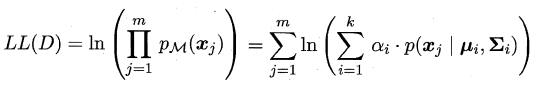
可以看出：简单的最大似然法根本无法求出所有的参数，这样PM也就没法计算。这里就要召唤出之前的EM大法，首先对高斯分布的参数及混合系数进行随机初始化，计算出各个PM（即γji，第i个样本属于j类），再最大化似然函数（即LL（D）分别对α、u和∑求偏导 ），对参数进行迭代更新。

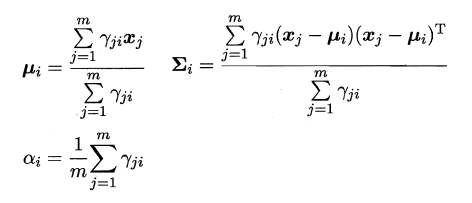
高斯混合聚类的算法流程如下图所示：