给定一个二分类数据集,正类标记为+1,负类标记为-1(对率回归中负类标记是0,这点是不同的)。
分类学习试图从样本空间中找到一个超平面,使得该超平面可以将不同类的样本分隔开。但是满足这样条件的平面可能有很多,哪一个才是最好的呢?
支持向量
在SVM中,我们试图找到处于两类样本正中间的超平面,因为这个超平面对训练数据局部扰动的容忍性最好,新样本最不容易被误分类。也就是说这个超平面对未见示例的泛化能力最强。
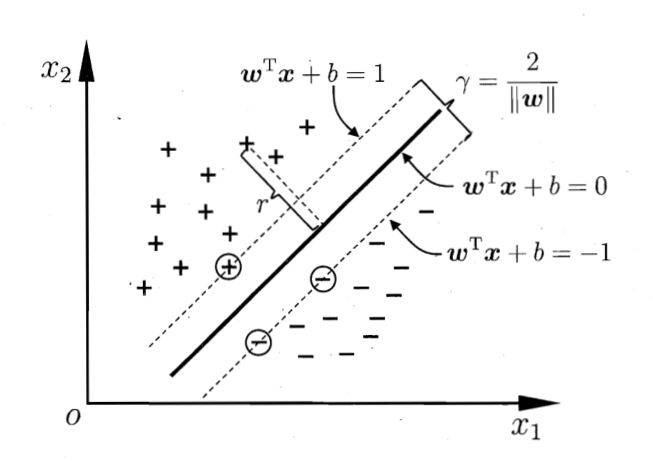
上图的实线就是划分超平面,在线性模型中可以通过方程 来描述,在二维样本空间中就是一条直线。
是线性模型的权重向量(又叫投影向量),也是划分超平面的法向量,决定着超平面的方向。偏置项
又被称为 位移项,决定了超平面和空间原点之间的距离。
假设超平面能够将所有训练样本正确分类,也即对于所有标记为+1的点有 ,所有标记为-1的点有
。只要这个超平面存在,那么我们必然可以对
和
进行适当的线性放缩,使得:
而SVM中定义使得上式等号成立的训练样本点就是支持向量(support vector)(如果叫作支持点可能更好理解一些,因为事实上就是样本空间中的数据点,但因为我们在表示数据点的时候一般写成向量形式,所以就称为支持向量),它们是距离超平面最近的几个样本点,也即上面图中两条虚线上的点(图中存在比支持向量距离超平面更近的点,这跟软间隔有关,这里先不讨论)。
在SVM中,我们希望实现的是最大化两类支持向量到超平面的距离之和,那首先就得知道怎么计算距离。
点到直线距离公式
假设直线方程为 ,那么有点到直线距离公式:
令 #card=math&code=%5Cmathbf%7Bw%7D%20%3D%20%28a%2Cb%29&id=esdLm),
#card=math&code=%5Cmathbf%7Bx%7D%20%3D%20%28x_1%2Cx_2%29&id=IIYw1),则可以把
写成向量形式
。把截距项设为
,则直线方程变为
,代入距离公式可得:
该式扩展到多维情况下也是通用的。
间隔
前面已经提到,希望实现的是最大化两类支持向量到超平面的距离之和,而根据定义,所有支持向量都满足:
代入前面的距离公式可以得到支持向量到超平面的距离为 。
定义间隔(margin)为两个异类支持向量到超平面的距离之和:
SVM的目标便是找到具有最大间隔(maximum margin)的划分超平面,也即找到使 最大的参数
和
:
%20%5Cgeq%201%2C%20%5Cquad%20%20i%3D1%2C2%2C…%2Cm%0A#card=math&code=%5Cmax_%7B%5Cmathbf%7Bw%7D%2Cb%7D%20%5Cfrac%7B2%7D%7B%5CVert%20%5Cmathbf%7Bw%7D%20%5CVert%7D%20%5Cquad%20s.t.%20%5Cquad%20y_i%28%5Cmathbf%7Bw%7D%5ET%5Cmathbf%7Bx%7D%2Bb%29%20%5Cgeq%201%2C%20%5Cquad%20%20i%3D1%2C2%2C…%2Cm%0A&id=ZwGXp)
约束部分指的是全部样本都被正确分类,此时标记值( 或
)乘上预测值(
或
)必定是一个
的数值。
看上去间隔大小只与 有关,但实际上位移项
也通过约束影响着
的取值,进而对间隔产生影响。
由于最大化 等价于最小化
,所以可以重写目标函数为:
%20%5Cgeq%201%2C%20%5Cquad%20%20i%3D1%2C2%2C…%2Cm%5Cqquad(1)%0A#card=math&code=%5Cmin_%7B%5Cmathbf%7Bw%7D%2Cb%7D%20%5Cfrac%7B1%7D%7B2%7D%20%5CVert%20%5Cmathbf%7Bw%7D%20%5CVert%5E2%20%5Cquad%20s.t.%20%5Cquad%20y_i%28%5Cmathbf%7Bw%7D%5ET%5Cmathbf%7Bx%7D%2Bb%29%20%5Cgeq%201%2C%20%5Cquad%20%20i%3D1%2C2%2C…%2Cm%5Cqquad%281%29%0A&id=fwODY)
引入 是为了求导时可以约去平方项的2,这便是支持向量机的基本型。
特别地,还有以下定义:
函数间隔:#card=math&code=y_i%28%5Cmathbf%7Bw%7D%5ET%5Cmathbf%7Bx%7D%2Bb%29&id=RDbpV)
几何间隔:%7D%7B%5CVert%20%5Cmathbf%7Bw%7D%20%5CVert%5E2%7D#card=math&code=%5Cfrac%7By_i%28%5Cmathbf%7Bw%7D%5ET%5Cmathbf%7Bx%7D%2Bb%29%7D%7B%5CVert%20%5Cmathbf%7Bw%7D%20%5CVert%5E2%7D&id=XIOZl)

