如何处理非线性划分
在现实任务中，我们更常遇到的是在原始样本空间中非线性可分的问题。对这样的问题，一种常用的思路是将样本从原始空间映射到一个更高维的特征空间，使得样本在该特征空间中线性可分。幸运的是，只要原始空间是有限维的（也即属性数目有限），那就必然存在一个高维特征空间使样本线性可分。
举个例子，二维平面上若干样本点呈如下分布：
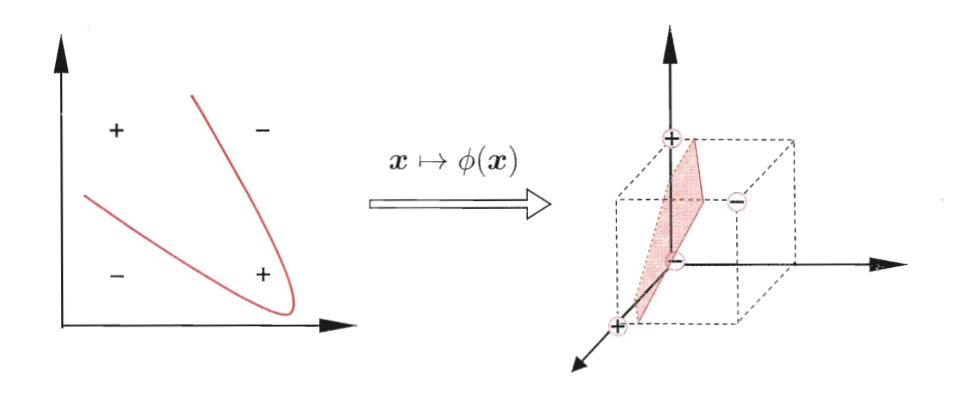
此时要划分两类样本，需要一个非线性的曲线。假设原始空间中两个属性是 
和 
，如果我们做一个映射，把样本点都映射到一个三维特征空间，可以看到这个时候，我们只需要一个线性超平面就可以将两类样本完全分开了，也就是说可以用前面的方法来求解了。
什么是核函数
在上面的例子中，我们是把每个样本对应的二维的特征向量 
映射为一个三维的特征向量，假设我们用 
#card=math&code=%5Cphi%28%5Cmathbf%7Bx%7D%29&id=Py2q5) 来表示映射所得的特征向量。则在映射的高维特征空间中，用于划分的线性超平面可以表示为：
%20%3D%20%5Cmathbf%7Bw%7D%5ET%20%5Cphi(%5Cmathbf%7Bx%7D)%20%2B%20b%0A#card=math&code=f%28%5Cmathbf%7Bx%7D%29%20%3D%20%5Cmathbf%7Bw%7D%5ET%20%5Cphi%28%5Cmathbf%7Bx%7D%29%20%2B%20b%0A&id=XLqoS)
类似式（1），可以得到此时的目标函数为：
%2Bb)%20%5Cgeq%201%2C%20%5Cquad%20%20i%3D1%2C2%2C…%2Cm%5Cqquad(9)%0A#card=math&code=%5Cmin_%7B%5Cmathbf%7Bw%7D%2Cb%7D%20%5Cfrac%7B1%7D%7B2%7D%20%5CVert%20%5Cmathbf%7Bw%7D%20%5CVert%5E2%20%5Cquad%20s.t.%20%5Cquad%20y_i%28%5Cmathbf%7Bw%7D%5ET%5Cphi%28%5Cmathbf%7Bx%7D%29%2Bb%29%20%5Cgeq%201%2C%20%5Cquad%20%20i%3D1%2C2%2C…%2Cm%5Cqquad%289%29%0A&id=fmFgD)
对应的对偶问题为：
%5ET%20%5Cphi(%5Cmathbf%7Bx%7Dj)%20%5Cquad%20s.t.%20%5Cquad%20%5Csum%7Bi%3D1%7D%5Em%20ai%20y_i%20%3D%200%2C%20%5Cquad%20a_i%20%5Cgeq%200%2C%20%5Cquad%20i%3D1%2C2%2C…%2Cm%20%5Cqquad%20(10)%0A#card=math&code=%5Cmax%7B%5Cmathbf%7Ba%7D%7D%20%5Csum%7Bi%3D1%7D%5Em%20a_i%20-%20%5Cfrac%7B1%7D%7B2%7D%20%5Csum%7Bi%3D1%7D%5Em%5Csum%7Bj%3D1%7D%5Em%20a_i%20a_j%20y_i%20y_j%20%5Cphi%28%5Cmathbf%7Bx%7D_i%29%5ET%20%5Cphi%28%5Cmathbf%7Bx%7D_j%29%20%5Cquad%20s.t.%20%5Cquad%20%5Csum%7Bi%3D1%7D%5Em%20a_i%20y_i%20%3D%200%2C%20%5Cquad%20a_i%20%5Cgeq%200%2C%20%5Cquad%20i%3D1%2C2%2C…%2Cm%20%5Cqquad%20%2810%29%0A&id=IJZRQ)
注意到对偶问题中，涉及到 
%5ET%20%5Cphi(%5Cmathbf%7Bx%7D_j)#card=math&code=%5Cphi%28%5Cmathbf%7Bx%7D_i%29%5ET%20%5Cphi%28%5Cmathbf%7Bx%7D_j%29&id=MCOvY) 的计算，也即 
和 
映射到高维特征空间后的内积（比如 
#card=math&code=x_i%20%3D%20%281%2C2%2C3%29&id=ebM0n)，
#card=math&code=x_j%20%3D%20%284%2C5%2C6%29&id=IdFjH)，那么内积 
就等于 
），由于特征空间维数可能很高，所以直接计算映射后特征向量的内积是很困难的，如果映射后的特征空间是无限维，根本无法进行计算。
为了解决这样的问题，就引入了核函数（kernel function）。
打个比方，假设输入空间是二维的，每个样本点有两个属性 
和 
，存在映射将每个样本点映射到三维空间：
%20%3D%20%5Cphi(x%2C%20y)%20%3D%20(x%5E2%2C%20%5Csqrt%7B2%7Dxy%2C%20y%5E2)%0A#card=math&code=%5Cphi%28%5Cmathbf%7Bx%7D%29%20%3D%20%5Cphi%28x%2C%20y%29%20%3D%20%28x%5E2%2C%20%5Csqrt%7B2%7Dxy%2C%20y%5E2%29%0A&id=s4otb)
给定原始空间中的两个样本点 
#card=math&code=%5Cmathbf%7Bv%7D_1%3D%28x_1%2Cy_1%29&id=xuMya) 和 
#card=math&code=%5Cmathbf%7Bv%7D_2%3D%28x_2%2Cy_2%29&id=hMCfs)，则它们映射到高维特征空间后的内积可以写作：
%5ET%20%5Cphi(%5Cmathbf%7Bv%7D_2)%20%26%3D%20%3C%5Cphi(%5Cmathbf%7Bv%7D_1)%2C%5Cphi(%5Cmathbf%7Bv%7D_2)%3E%5C%5C%0A%26%3D%3C(x_1%5E2%2C%20%5Csqrt%7B2%7Dx_1y_1%2C%20y_1%5E2)%2C(x_2%5E2%2C%20%5Csqrt%7B2%7Dx_2y_2%2C%20y_2%5E2)%3E%5C%5C%0A%26%3D%20x_1%5E2x_2%5E2%20%2B%202x_1x_2y_1y_2%20%2B%20y_1%5E2y_2%5E2%5C%5C%0A%26%3D%20(x_1x_2%20%2B%20y_1y_2)%5E2%5C%5C%0A%26%3D%20%3C%5Cmathbf%7Bv%7D_1%2C%5Cmathbf%7Bv%7D_2%3E%5E2%5C%5C%0A%26%3D%20%5Ckappa(%5Cmathbf%7Bv%7D_1%2C%5Cmathbf%7Bv%7D_2)%5C%5C%0A%5Cend%7Bsplit%7D#card=math&code=%5Cbegin%7Bsplit%7D%0A%5Cquad%20%5Cphi%28%5Cmathbf%7Bv%7D_1%29%5ET%20%5Cphi%28%5Cmathbf%7Bv%7D_2%29%20%26%3D%20%3C%5Cphi%28%5Cmathbf%7Bv%7D_1%29%2C%5Cphi%28%5Cmathbf%7Bv%7D_2%29%3E%5C%5C%0A%26%3D%3C%28x_1%5E2%2C%20%5Csqrt%7B2%7Dx_1y_1%2C%20y_1%5E2%29%2C%28x_2%5E2%2C%20%5Csqrt%7B2%7Dx_2y_2%2C%20y_2%5E2%29%3E%5C%5C%0A%26%3D%20x_1%5E2x_2%5E2%20%2B%202x_1x_2y_1y_2%20%2B%20y_1%5E2y_2%5E2%5C%5C%0A%26%3D%20%28x_1x_2%20%2B%20y_1y_2%29%5E2%5C%5C%0A%26%3D%20%3C%5Cmathbf%7Bv%7D_1%2C%5Cmathbf%7Bv%7D_2%3E%5E2%5C%5C%0A%26%3D%20%5Ckappa%28%5Cmathbf%7Bv%7D_1%2C%5Cmathbf%7Bv%7D_2%29%5C%5C%0A%5Cend%7Bsplit%7D&id=UCAsP)
可以看到在这个例子里，高维特征空间中两个点的内积，可以写成一个关于原始空间中两个点的函数 
#card=math&code=%5Ckappa%28%5Ccdot%3B%5Ccdot%29&id=sbhHe)，这就是核函数。
特别地，上面的例子中，映射用的是多项式核，多项式的次数 
取2。
为什么需要核函数
这里的例子为了计算方便，映射的空间维数依然很低，这里稍微解释一下为什么需要核函数？假设原始空间是二维的，那么对于两个属性 
和 
，取一阶二阶的组合只有5个（也即 
，
，
，
，
）。但当原始空间是三维的时候，仍然取一阶二阶，组合就多达19个了（也即 
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
）。随着原始空间维数增长，新空间的维数是呈爆炸性上升的。何况现实中我们遇到的问题的原始空间往往本来就已经是高维的，如果再进行映射，新特征空间的维度是难以想象的。
然而有了核函数，我们就可以在原始空间中通过函数 #card=math&code=%5Ckappa%28%5Ccdot%3B%5Ccdot%29&id=cQW6J) 计算（这称为核技巧（kernel trick）），而不必直接计算高维甚至无穷维特征空间中的内积。
使用核函数后，对偶问题式（10）可以重写为：
%20%5Cquad%20s.t.%20%5Cquad%20%5Csum%7Bi%3D1%7D%5Em%20a_i%20y_i%20%3D%200%2C%20%5Cquad%20a_i%20%5Cgeq%200%2C%20%5Cquad%20i%3D1%2C2%2C…%2Cm%20%5Cqquad%20(11)%0A#card=math&code=%5Cmax%7B%5Cmathbf%7Ba%7D%7D%20%5Csum%7Bi%3D1%7D%5Em%20a_i%20-%20%5Cfrac%7B1%7D%7B2%7D%20%5Csum%7Bi%3D1%7D%5Em%5Csum%7Bj%3D1%7D%5Em%20a_i%20a_j%20y_i%20y_j%20%5Ckappa%28%5Cmathbf%7Bx%7D_i%3B%5Cmathbf%7Bx%7D_j%29%20%5Cquad%20s.t.%20%5Cquad%20%5Csum%7Bi%3D1%7D%5Em%20a_i%20y_i%20%3D%200%2C%20%5Cquad%20a_i%20%5Cgeq%200%2C%20%5Cquad%20i%3D1%2C2%2C…%2Cm%20%5Cqquad%20%2811%29%0A&id=K1Yfm)
求解后得到的模型可以表示为：
%20%26%3D%20%5Cmathbf%7Bw%7D%5ET%20%5Cphi(%5Cmathbf%7Bx%7D)%20%2B%20b%5C%5C%0A%26%20%3D%20%5Csum%7Bi%3D1%7D%5Em%20a_i%20y_i%20%5Cphi(%5Cmathbf%7Bx%7D_i)%5ET%20%5Cphi(%5Cmathbf%7Bx%7D)%20%2B%20b%5C%5C%0A%26%20%3D%20%5Csum%7Bi%3D1%7D%5Em%20ai%20y_i%20%5Ckappa(%5Cmathbf%7Bx%7D_i%3B%5Cmathbf%7Bx%7D)%20%2B%20b%0A%5Cend%7Bsplit%7D#card=math&code=%5Cbegin%7Bsplit%7D%0Af%28%5Cmathbf%7Bx%7D%29%20%26%3D%20%5Cmathbf%7Bw%7D%5ET%20%5Cphi%28%5Cmathbf%7Bx%7D%29%20%2B%20b%5C%5C%0A%26%20%3D%20%5Csum%7Bi%3D1%7D%5Em%20ai%20y_i%20%5Cphi%28%5Cmathbf%7Bx%7D_i%29%5ET%20%5Cphi%28%5Cmathbf%7Bx%7D%29%20%2B%20b%5C%5C%0A%26%20%3D%20%5Csum%7Bi%3D1%7D%5Em%20a_i%20y_i%20%5Ckappa%28%5Cmathbf%7Bx%7D_i%3B%5Cmathbf%7Bx%7D%29%20%2B%20b%0A%5Cend%7Bsplit%7D&id=o8WSO)
这条式子表明了模型最优解可通过训练样本的核函数展开，称为支持向量展式（support vector expansion）。
在需要对新样本进行预测时，我们无需把新样本映射到高维（甚至无限维）空间，而是可以利用保存下来的训练样本（支持向量）和核函数 
进行求解。
注意，核函数本身不等于映射！！！它只是一个与计算两个数据点映射到高维空间之后的内积等价的函数。
当我们发现数据在原始空间线性不可分时，会有把数据映射到高维空间来实现线性可分的想法，比方说引入原有属性的幂或者原有属性之间的乘积作为新的维度。假设我们把数据点都映射到了一个维数很高甚至无穷维的特征空间，而模型求解和预测的过程需要用到映射后两个数据点的内积，这时直接计算就没辙了。但我们又幸运地发现，原来高维空间中两点的内积在数值上等于原始空间通过某个核函数算出的函数值，无需先映射再求值，就很好地解决了计算的问题了。
核函数的性质
核函数定理：给定一个输入空间 
，函数 #card=math&code=%5Ckappa%28%5Ccdot%3B%5Ccdot%29&id=B0spB) 是定义在 
上的对称函数。当且仅当对于任意数据集 
, 对应的核矩阵（kernel matrix）都是半正定的时候，
是核函数。
核矩阵是一个规模为 
的函数矩阵，每个元素都是一个函数，比如第 
行 
列的元素是 
#card=math&code=%5Ckappa%28%5Cmathbf%7Bx%7D_i%2C%5Cmathbf%7Bx%7D_j%29&id=vUIgx)。也即是说，任何一个核函数都隐式地定义了一个称为“再生核希尔伯特空间（Reproducing Kernel Hilbert Space，简称RKHS）”的特征空间。
做映射的初衷是希望样本在新特征空间上线性可分，新特征空间的好坏直接决定了支持向量机的性能，但是我们并不知道怎样的核函数是合适的。一般来说有以下几种常用核函数：
| 名称 |
表达式 |
参数 |
| 线性核 |
%3D%5Cmathbf%7Bx%7D_i%5ET%5Cmathbf%7Bx%7D_j#card=math&code=%5Ckappa%28%5Cmathbf%7Bx%7D_i%2C%5Cmathbf%7Bx%7D_j%29%3D%5Cmathbf%7Bx%7D_i%5ET%5Cmathbf%7Bx%7D_j&id=RyPWT) |
- |
| 多项式核 |
%3D(%5Cmathbf%7Bx%7D_i%5ET%5Cmathbf%7Bx%7D_j)%5Ed#card=math&code=%5Ckappa%28%5Cmathbf%7Bx%7D_i%2C%5Cmathbf%7Bx%7D_j%29%3D%28%5Cmathbf%7Bx%7D_i%5ET%5Cmathbf%7Bx%7D_j%29%5Ed&id=aAcDL) |
 为多项式的次数，d=1时退化为线性核 |
| 高斯核（亦称RBF核） |
%3D%5Cexp%20(-%5Cfrac%7B%5CVert%20%5Cmathbf%7Bx%7D_i-%5Cmathbf%7Bx%7D_j%20%5CVert%20%5E2%7D%7B2%5Csigma%5E2%7D)#card=math&code=%5Ckappa%28%5Cmathbf%7Bx%7D_i%2C%5Cmathbf%7Bx%7D_j%29%3D%5Cexp%20%28-%5Cfrac%7B%5CVert%20%5Cmathbf%7Bx%7D_i-%5Cmathbf%7Bx%7D_j%20%5CVert%20%5E2%7D%7B2%5Csigma%5E2%7D%29&id=xz3x9) |
 为高斯核的带宽（width） |
| 拉普拉斯核 |
%3D%5Cexp%20(-%5Cfrac%7B%5CVert%20%5Cmathbf%7Bx%7D_i-%5Cmathbf%7Bx%7D_j%20%5CVert%7D%7B%5Csigma%7D)#card=math&code=%5Ckappa%28%5Cmathbf%7Bx%7D_i%2C%5Cmathbf%7Bx%7D_j%29%3D%5Cexp%20%28-%5Cfrac%7B%5CVert%20%5Cmathbf%7Bx%7D_i-%5Cmathbf%7Bx%7D_j%20%5CVert%7D%7B%5Csigma%7D%29&id=BmFJg) |
 |
| Sigmoid核 |
%3D%5Ctanh(%5Cbeta%20%5Cmathbf%7Bx%7D_i%5ET%5Cmathbf%7Bx%7D_j%2B%5Ctheta)#card=math&code=%5Ckappa%28%5Cmathbf%7Bx%7D_i%2C%5Cmathbf%7Bx%7D_j%29%3D%5Ctanh%28%5Cbeta%20%5Cmathbf%7Bx%7D_i%5ET%5Cmathbf%7Bx%7D_j%2B%5Ctheta%29&id=epMo7) |
 为双曲正切函数， |
特别地，文本数据一般用线性核，情况不明可尝试高斯核。
除了这些常用的核函数，要产生核函数还可以使用组合的方式：
- 若
和 
都是核函数，则 
也是核函数，其中 
。 - 若
和 
都是核函数，则其直积 
%20%3D%20%5Ckappa_1(%5Cmathbf%7Bx%7D%2C%5Cmathbf%7Bz%7D)%5Ckappa_2(%5Cmathbf%7Bx%7D%2C%5Cmathbf%7Bz%7D)#card=math&code=%5Ckappa_1%20%5Cotimes%20%5Ckappa_2%28%5Cmathbf%7Bx%7D%2C%5Cmathbf%7Bz%7D%29%20%3D%20%5Ckappa_1%28%5Cmathbf%7Bx%7D%2C%5Cmathbf%7Bz%7D%29%5Ckappa_2%28%5Cmathbf%7Bx%7D%2C%5Cmathbf%7Bz%7D%29&id=vHXfe) 也是核函数。 - 若
是核函数，则对于任意函数 
#card=math&code=g%28%5Cmathbf%7Bx%7D%29&id=lGUGe)，
%20%3D%20g(%5Cmathbf%7Bx%7D)%20%5Ckappa_1(%5Cmathbf%7Bx%7D%2C%5Cmathbf%7Bz%7D)%20g(%5Cmathbf%7Bz%7D)#card=math&code=%5Ckappa%28%5Cmathbf%7Bx%7D%2C%5Cmathbf%7Bz%7D%29%20%3D%20g%28%5Cmathbf%7Bx%7D%29%20%5Ckappa_1%28%5Cmathbf%7Bx%7D%2C%5Cmathbf%7Bz%7D%29%20g%28%5Cmathbf%7Bz%7D%29&id=eyXVz) 也是核函数。
