假设检验

假设检验中的假设是对学习器泛化错误率分布的某种判断或者猜想。直观上，测试错误率与泛化错误率相差不大，可以根据测试错误率推出泛化错误率。

在进行比较检验前，完成了一次模型预测，已知测试错误率为。

一个泛化错误率为 的模型在 m 个样本上预测错 m’个样本的概率为：

，这个概率符合二项分布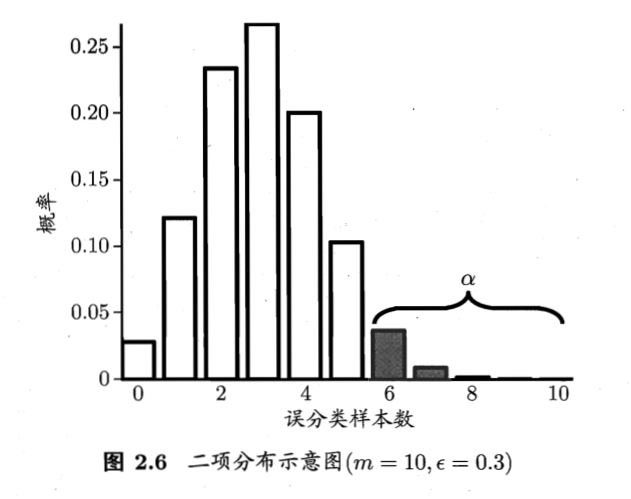

又因为已知测试错误率为，也即知道了该模型在m个样本上实际预测错了 个样本。代入公式，对求偏导会发现，给定这些条件时，的概率是最大的。

二项检验（binomial test）

假设泛化错误率，并且设定置信度为 。则可以这样定义错误率的阈值 ：

其中表示左式在右边条件满足时成立。右式计算的是发生不符合假设的事件的总概率，如果我们要有 的把握认为假设成立，那么发生不符合假设的事件的总概率就必须低过 。

在满足右式的所有中，选择最大的作为阈值。如果在测试集中观测到的测试错误率是小于阈值 的， 我们就能以 的把握认为假设成立，即该模型的泛化误差。

t检验

二项检验只用于检验某一次测试的性能度量，但实际任务中我们会进行多次的训练/测试，得到多个测试错误率，比方说进行了k次测试，得到 ,, … 。这次就会用到t检验(t-test)。

定义这 k 次测试的平均错误率 和方差：





注意！这里使用的是无偏估计的样本方差，分母是 k-1，因为当均值确定，并且已知 k-1个样本的值时，第 k个样本的值是可以算出来的，也可以说是受限的。

假设泛化错误率 ，并且设定显著度为 。计算统计量t：



该统计量服从自由度 k-1的t分布，如下图：



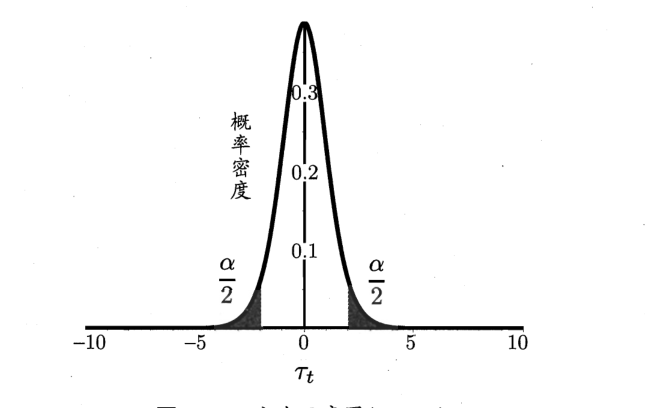
自由度越大，约接近于正态分布，自由度为无穷大时变为标准正态分布（，）。

如果计算出的t统计量落在临界值范围 [,] 之内（注：临界值由自由度 k和显著度 决定，通过查表得出），我们就能以 的把握认为假设成立，即该模型的泛化误差 。