5.1 迭代型Spark应用的分类及特点
迭代型Spark应用是指运行在Spark上,需要进行不断迭代才能得到最终结果的应用。
(1)迭代型Spark应用有哪些?
迭代型Spark应用主要包括机器学习应用和图计算应用。这两类应用都需要在数据上不断迭代计算、不断更新中间状态,最终达到一个收敛的结果。
(2)迭代型应用和非迭代型应用的编程方法有什么不同?
迭代型应用通常与算法结合较为紧密,有固定的计算流程。
(3)迭代型应用的逻辑处理流程和物理执行计划与非迭代型应用有哪些不同?
因为迭代型应用包含迭代计算,所以相应的Spark job个数或stage个数一般比非迭代型应用多,而且这些job和stage中很多是重复出现的。另外,在迭代计算的过程中,有些输入数据和中间数据常常是可以重复使用的,因此迭代型应用会比非迭代型应用更多地使用数据缓存。
5.2 迭代型机器学习应用SparkLR
5.2.1 应用描述
SparkLR是经典机器学习算法Logistic Regression的Spark分布式版本,可以在Spark项目自带的例子(Spark example包)中找到。
5.2.2 算法原理
Logistic Regression分类模型的数学表达式为:
其中w是一个参数向量,其值需要对模型不断训练得到。对于每个新样例,将其特征向量
代入
后,会得到
对应的分类结果为
的概率,如下:
当的分类类别为1的概率超过50%时,我们认为为正类。直观地说,这是因为
是一个Sigmoid函数。图5.1中Sigmoid的值域是(0,1),可以用来表示概率,进而可以用于表示
属于类别为1的概率。
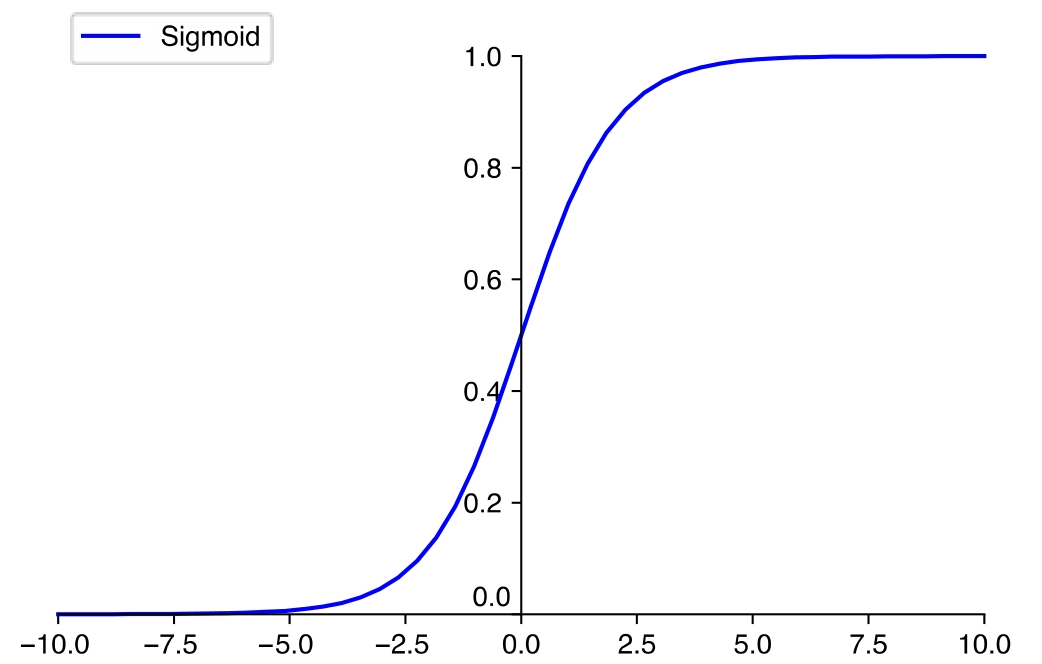
图5.1 Sigmoid函数图_
实际应用中Logistic Regression选取w的标准是使得正确预测每个样例的概率的乘积最大。如果采用形式化表示,就是使得下面的代代价函数
的值最大。这种方法被称为“最大似然估计”方法。
因为指数形式乘积的值可能会过小,所以我们对函数L(w)取对数:
在实际应用中,Logistic Regerssion通常采用下面所述的梯度下降法来求解w。
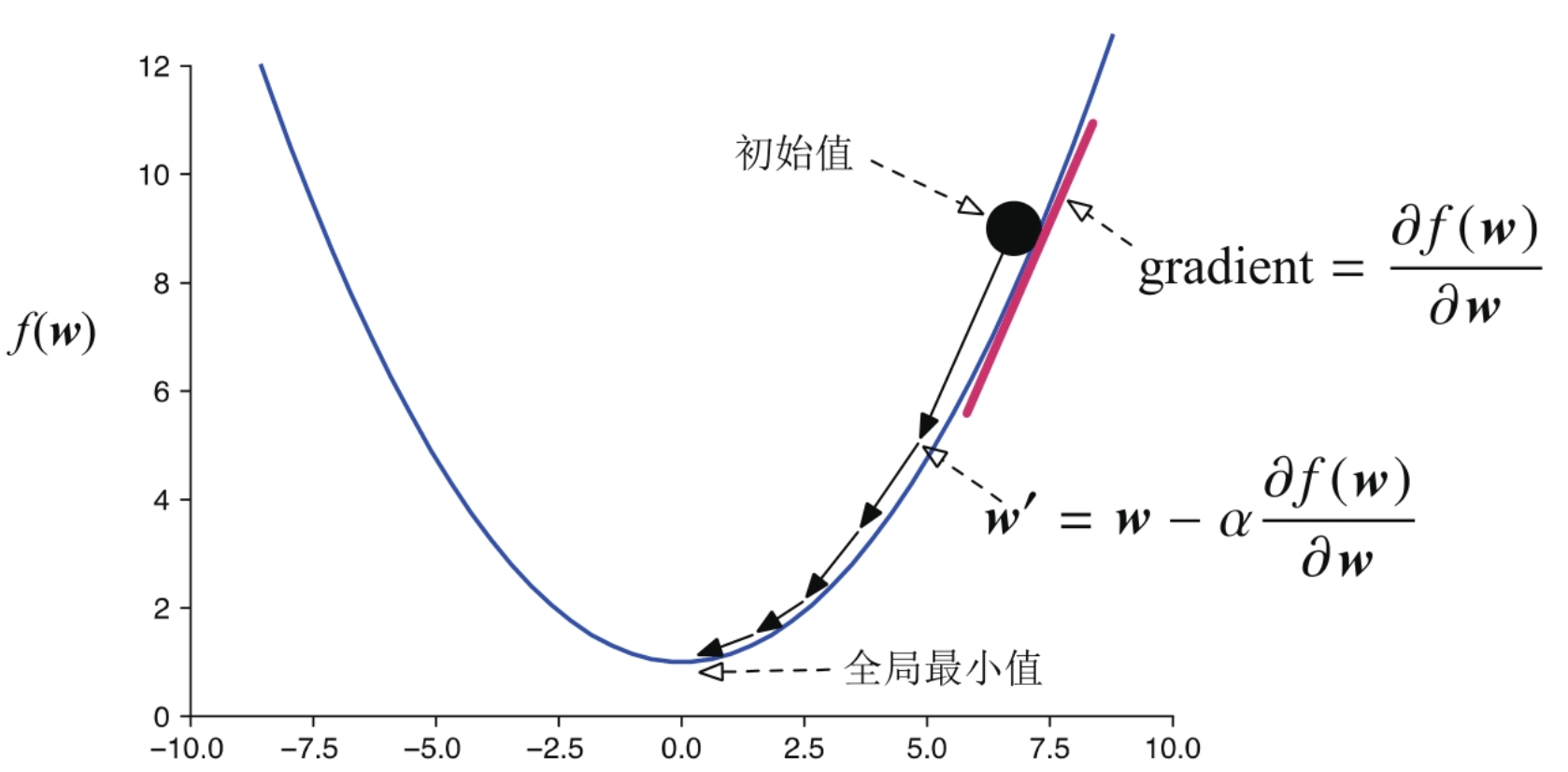
图5.2 梯度下降法图示
w的更新公式如下,其中α固定为1。
_
5.2.3 基于Spark的并行化实现
Logistic Regression模型的训练过程主要包含两个计算步骤:一是根据训练数据计算梯度,二是更新模型参数向量w。计算梯度(gradient)时需要读入每个样例,代入梯度公式计算,并对计算结果进行加和。由于在计算时每个样例可以独立代入公式,互相不影响,所以我们可以采用“数据并行化”的方法,即将训练样本划分为多个部分,每个task只计算部分样例上的梯度,然后将这些梯度进行加和得到最终的梯度。在更新参数向量w时,更新操作可以在一个节点上完成,不需要并行化。
我们可以画出SparkLR的并行化逻辑处理流程,如图5.3所示。
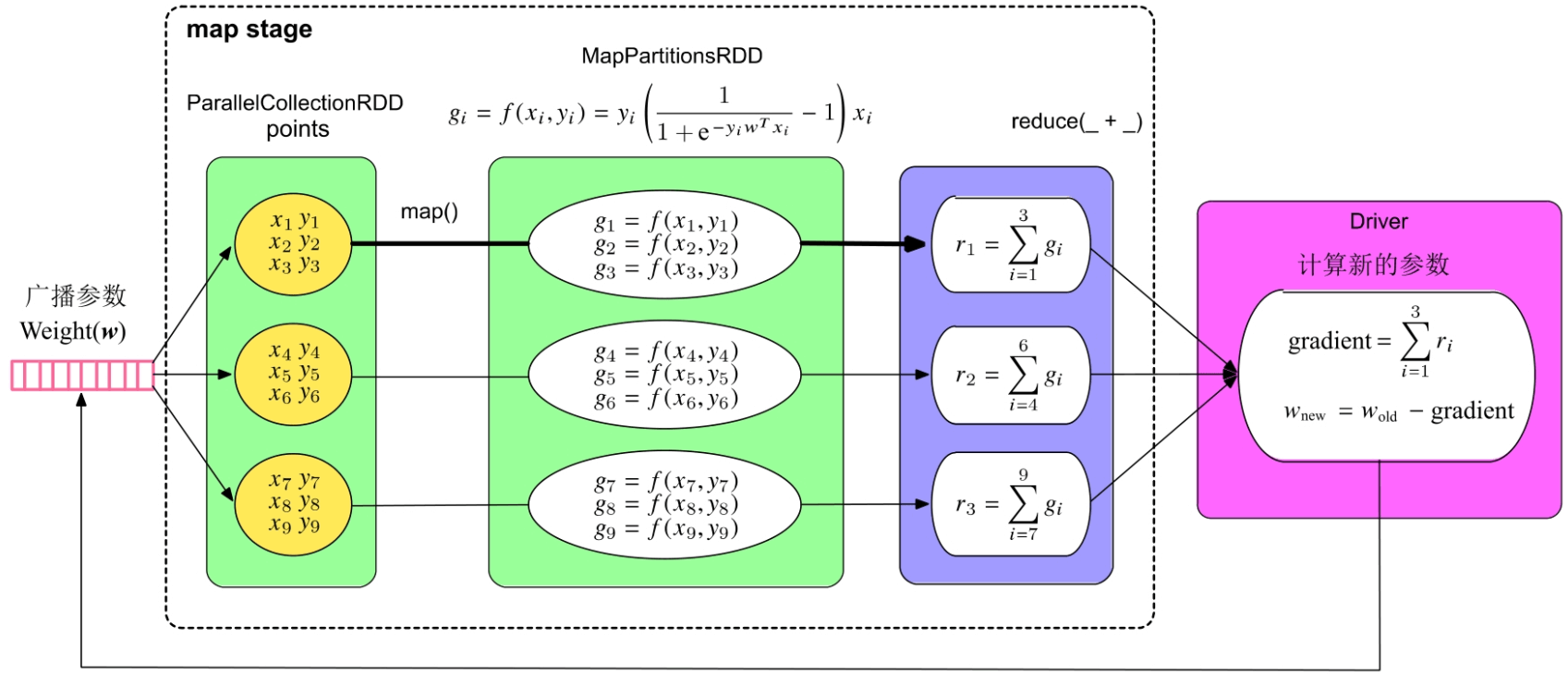
图5.3 迭代型机器学习应用SparkLR的并行化逻辑处理流程
在本例中使用的reduce()操作与reduceByKey()操作不同,reduce()是action()操作,并不会形成reduce stage,因此,SparkLR只包含一个不断重复运行的map stage。
SparkLR在实际运行时生成什么样的job和stage呢?当我们把迭代轮数设为5时,形成的job和stage如图5.4所示。可以看到在这个例子中,SparkLR一共生成了5个job,每个job只包含一个map stage。一个有趣的现象是,第1个job运行需要0.8s(800 ms),而第2个到第5个job只需要56~76ms。发生这一现象的原因是,SparkLR在第1个job运行时对训练数据(points:RDD)进行了缓存,使得后续的job只需要从内存中直接读取数据进行计算即可,这大大减小了数据加载到内存中的开销,从而加速了计算过程。在第7章中我们会详细讨论Spark缓存机制的设计和实现。
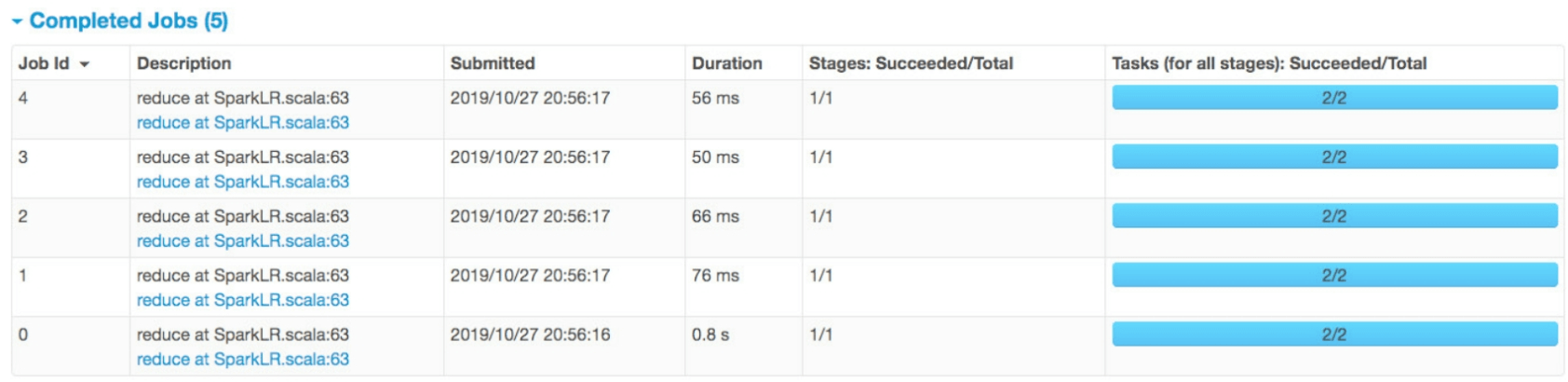
图5.4 SparkLR产生的job和stage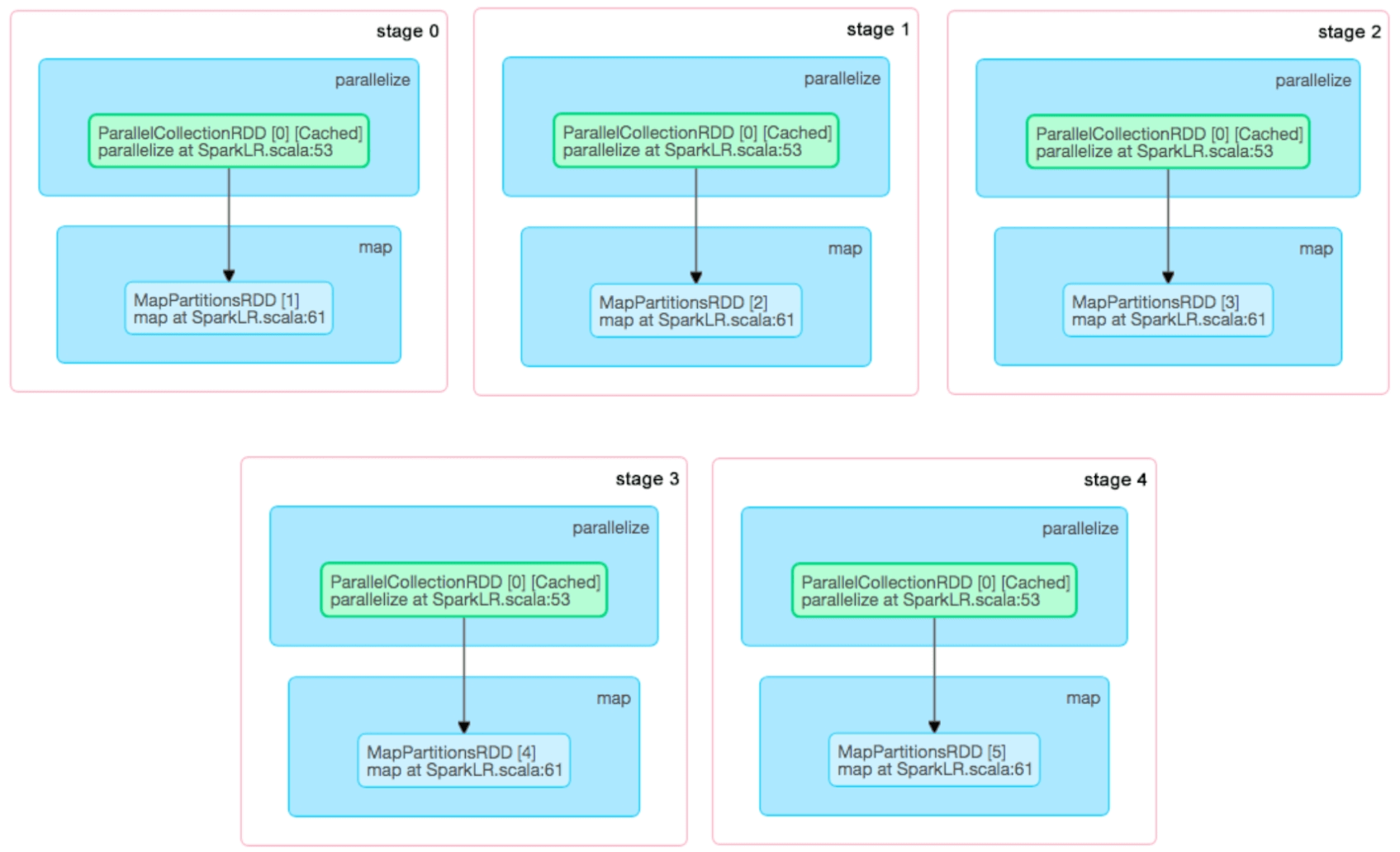
图5.4 SparkLR产生的job和stage(续)_
5.2.4 深入讨论
如果直接将SparkLR的实现方法应用于大规模数据训练,则还存在不少系统性能问题。
(1)数据聚合问题
为了将所有task计算的梯度进行加和,SparkLR使用了reduce()操作,这个操作需要将所有task的计算结果收集到Driver端进行统一聚合计算。尽管reduce()操作会提前(在task运行结束前)对每个record对应的梯度进行本地聚合,以减少数据传输量,但如果task过多且每个task本地聚合后的结果(单个graident)过大,那么统一传递到Driver端仍然会造成单点的网络瓶颈等问题。为了解决这一问题,Spark设计了性能更好的treeAggregate()操作,使用树形聚合方法来减少网络和计算延迟。我们将在下一个例子中详细介绍这一优化措施。
(2)参数存储问题
在SparkLR例子中,我们将w的维度设置为10,然而在大规模互联网应用中,w的维度可能是千万甚至上亿。这么大的模型参数会导致单点内存瓶颈问题,即在Driver端对w进行存储和计算可能会出现内存溢出、计算时间过长等性能和可靠性问题。为了解决这一问题,学术界和工业界提出了参数服务器的解决方案。但Spark目前还没有提供参数服务器的官方实现。
5.3 迭代型机器学习应用——广义线性模型
广义线性模型(GLM)统一了多种线性分类和回归模型,包括用于分类的Logistic Regression、Linear SVM模型,以及用于回归的Linear Regression、Lasso Regression、Ridge Regression模型等。那么,为什么可以将这些模型进行统一呢?原因是这些模型要解决的问题都可以被抽象为一个凸优化问题,而且模型的计算过程基本相同,不同点只是这些模型具有不同的计算函数(代价函数和梯度计算公式)。Spark通过对这些模型的计算过程进行抽象统一,同时支持不同的计算函数,可以实现广义线性模型。在此基础上,通过实现不同的计算函数就可以构建不同的模型。这样可以避免在Spark中实现不同模型算法的重复性。
线性分类和回归问题可以被抽象为一个凸优化问题,即找到一个合适的参数向量w来使下面的代价函数最小化:
是一个凸函数,包含两部分
和
。其中,
是正则化项,用来控制模型的复杂度,避免模型过拟合;
是损失函数,用来衡量模型的预测结果与实际结果的差距。
可以看作是以
和y为输入的函数,其中w是需要求解的参数向量。λ是一个大于等于零的固定参数,用来调整
和
的比例,即决定优化目标是更强调减少模型复杂度的(结构风险最小化)还是更强调减少训练误差(经验风险最小化)的。取较大的λ值将较大程度约束模型复杂度,反之,更强调减少训练误差。
这里需要计算相对于w的梯度。由于
包含正则化和损失函数两项,所以这里的梯度包含
相对于w的梯度
,以及
相对于w的梯度
。

表5.5 不同线性模型的损失函数及其梯度计算公式

表5.6 不同线性模型使用的正则化项及其梯度计算公式
直观上来说,L2正则化的作用是使得w的各维度值变得更平滑均衡,即将某些趋近于0的维度值变得大一些,同时将较大的维度值变得小一些。而L1正则化的作用是使得参数向量w中的维度值更加稀疏,也就是使得某些维度更趋近于0,从而避免不太重要的特征参与计算。另外,有些正则化方法可以兼顾L1正则化和L2正则化的优点,如Elastic net正则化,直观上来讲Elastic net正则化是L2和L1正则化的插值。
在得到相对于w的梯度后,我们可以使用w的计算公式,对w进行迭代更新,具体公式为:
这里再具体介绍一下不同线性机器学习模型的含义和为什么会这样选择。
(1)Logistic Regression(LR)分类模型
Logistic Regression的算法原理,这里为了约束模型的复杂度,添加了正则化项。由于Logistic Regression算法本身的目标是减少训练误差(经验风险最小化),所以可以搭配不同的结构风险最小化方法,如L2、L1和Elastic net正则化。
(2)Linear SVM分类模型
SVM算法的目标是最大化样本数据到分类超平面的间隔距离,即最小化,该目标函数与L2正则化的形式一致,因此SVM目标函数本身包含L2正则化,只需要考虑如何选择损失函数。因为Hinge loss损失函数可以较为精确地评价SVM模型的预测值与实际值误差,所以SVM选择使用Hinge loss损失函数。注意,如果我们强制把SVM中的L2正则化项替换为L1正则化项,就变成了线性规划问题。
(3)回归模型
3种回归模型都使用平方损失函数来度量预测值和实际值的误差,不同的是Linear Regression不使用正则化,Lasso Regression使用L1正则化,而Ridge Regression使用L2正则化。
5.3.2 基于Spark的并行化实现
对比广义线性模型与Logistic Regression的算法原理可以发现,两者的迭代计算过程是一样的,只是代价函数和梯度计算公式有所差别。因此,我们仍然可以采用数据并行化方法在Spark上实现广义线性模型。因为SparkLR实现方案还存在性能瓶颈,所以需要进一步优化。另外,需要为不同的广义线性模型变换梯度计算公式。下面,我们以问题的形式讨论在Spark上实现广义线性模型的具体流程和这样设计背后的原理。
(1)如何对w进行初始化?
在迭代开始时,在Driver端使用全零值或者任意随机值对w向量进行初始化。
(2)怎么划分训练数据?
采用水平划分方法,将包含n个样例的训练数据水平切分为m块,每一块包含的样例个数为ni。如图5.7所示,第1个分块中的样例个数为。如果这些输入数据存放在HDFS上,则默认每块数据大小为128MB。
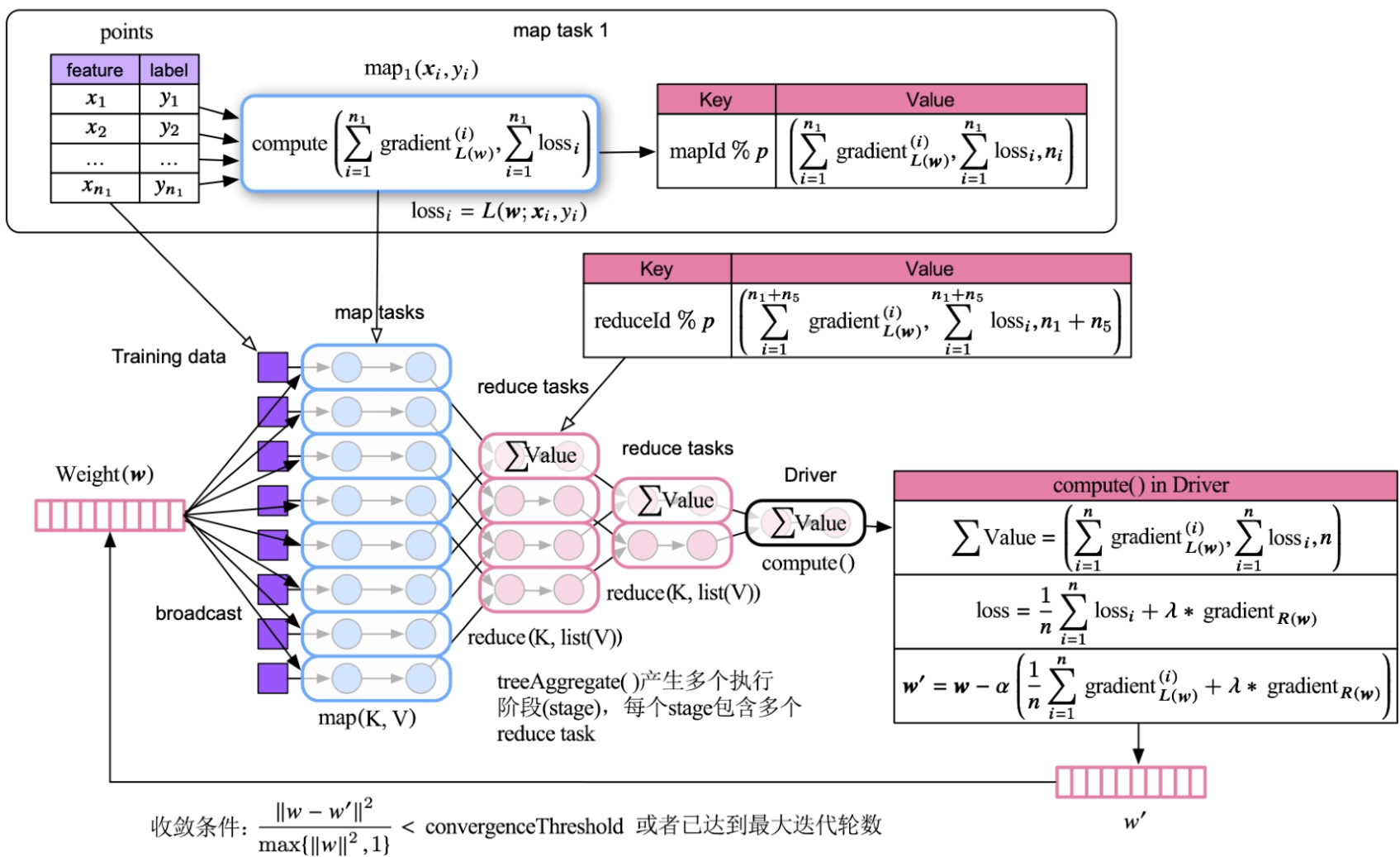
图5.7 广义线性模型的并行化迭代处理流程
(3)迭代的主要步骤是什么?
广义线性模型训练过程与Logistic Regression的训练过程类似,每轮迭代主要包含两步:第1步是计算梯度和
,第2步是对w进行如下更新。不断重复这个过程,直至收敛。
(4)如何并行化迭代过程?
上述的迭代步骤中,主要耗时在计算上,那么如何对其并行化?由于在每个样例
上计算
是可以独立进行的,所以可以采用数据并行化方法,也就是让每个task计算一部分样本数据上的
,然后统一累加得到
。
(5)如何更新参数w?
Driver端收集到所有task输出的梯度和损失等信息,将梯度进行累加得到,然后根据正则化项的梯度公式
及w的更新公式来对w进行更新。这里也对损失进行了累加,目的是记录
损失的变化过程,即迭代过程中训练误差的波动情况,用于后续的参数调优。在代码实现中,w是一个可变的向量变量,类型为DenseVector,采用Double数组实现,一直存放在Driver端的内存中。在每轮迭代开始时,Spark将向量变量w进行序列化,并广播到每个map task中。
我们进一步讨论其物理执行计划的一些细节问题:
- 在每轮迭代开始前,Spark将参数向量w的最新值广播到每个map task(确切说是task所在的Executor)中,然后每个task将其存放在本地内存中。如果w很大,则需要消耗大量内存空间。
- 使用treeAggregate()虽然可以解决Driver端单点数据聚合效率低下、内存不足等问题,但是会引入更多的stage和task,而且随着stage增加,越靠下游的stage,其可并行执行的task个数越小。这样,并行化程度不断降低将影响整体执行的效率。为了解决这个问题,Spark默认将树的层数设为两层,这样可以避免太多的执行阶段。
- 广义线性模型产生的Shuffle数据量很少。如图5.7所示,在广义线性模型的并行计算过程中,每个map/reduce task只输出一个record(梯度的累加值)。Shuffle阶段将这些task输出的record以round-robin的方式发送到下一阶段的task。为了实现round-robin的分发方式,record 的Key 被设计为taskId对下一阶段中task 个数(p)的取模,record的Value被设计为梯度的累加值。
- Driver端需要对w向量和gradient进行运算,如果训练数据的特征维度很高的话,则需要大量内存。
5.3.3 深入讨论
目前,基于Spark对机器学习进行并行化实现还存在不少问题。
(1)大规模参数存储问题
(2)计算同步问题
目前Spark迭代更新w参数的方法属于同步更新,即Spark需要等待所有的map/reduce task计算完成并得到最终的梯度后,再更新w。当一个stage中的task运行速速度不一样时,需要等待慢的task完成后才能进行下一步计算,这样会导致计算延迟。
对于一些大规模机器学习应用,其模型训练过程需要迭代上百轮,甚至上千轮,这个等待延迟就会很长。当某些task失败需要重启时,带来的计算延时更长。
如果采用异步更新,即允许运行快的task使用还未更新的w进行下一轮计算,虽然可以加快计算速度,但是由于异步更新会使用旧的参数进行迭代计算,则会造成收敛速度慢等问题。为了平衡计算速度和收敛速度,一些学者提出了半异步更新协议SSP,该方法的核心思想是允许在一定时限内使用旧的参数进行计算,即参数“旧”的程度不能超过m轮。此方法可以在一定程度上缓解同步更新等待时延长和异步更新收敛速度慢的问题,然而还不能从根本上解决问题,更具体的细节可以参考相关论文。
(3)task的频繁启停问题
每轮迭代都需要启动和停止task,如果迭代轮数太多,则也会带来比较长的延迟。一个可能的解决方案是采用task重用技术,即task一直运行,每接收到新的数据和请求,就立即开始计算来降低延迟。
5.4 迭代型图计算应用——PageRank
5.4.1 应用描述
PageRank可以被用于度量节点重要性,是网页排序的经典算法。在基于PageRank的网页排序中,一个节点(网站)被链接的次数越多,说明该节点越重要。
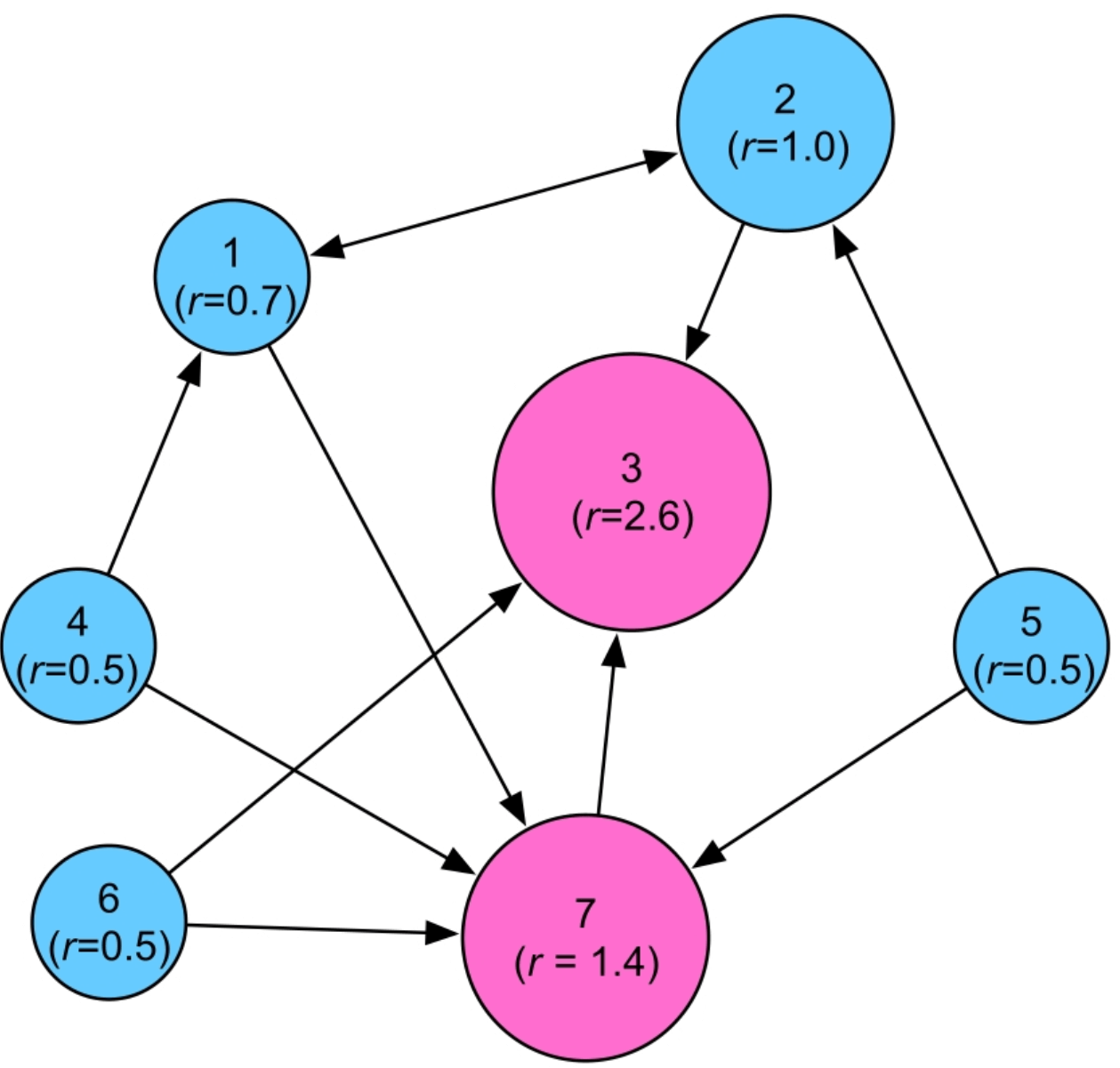
图5.8 PageRank算法示例,节点的rank (r)值越大节点越重要
从编程角度来说,PageRank计算主要包含以下3个步骤:
- 初始化每个节点的rank值(如1.0)。
- 将每个节点的rank值传递给其邻居节点。
- 每个节点根据所有邻居发送来的rank值计算和更新自身的rank值。
不断重复和迭代上述后两个步骤,直至每个节点的rank值不再改变或者改变的值很小。当图的规模很大时,图的存储和迭代计算代价将会很高,因此基于集群的并行化处理变得非常必要。接下来我们将讨论如何在Spark上实现PageRank算法的并行化。
5.4.2 基于Spark的并行化实现
如何对大规模图算法进行并行化处理是一个重要的研究问题,目前并行化的主要思想是将大图切分为多个子图,然后将这些子图分布到不同机器上进行并行计算,在必要时进行跨机器通信同步计算得出结果。学术界和工业界提出了多种将大图切分为子图的图划分方法,主要包含两种:边划分(Edge Cut)和点划分(Vertex Cut)。
边划分
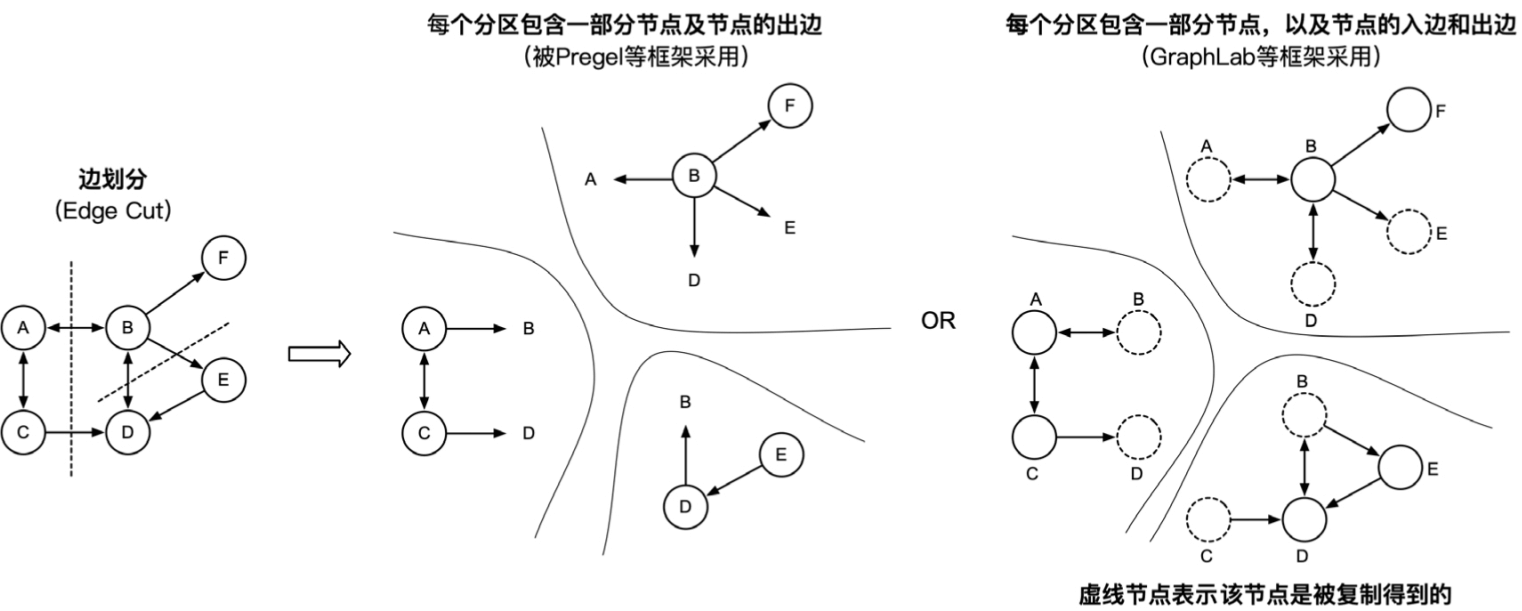
图5.9 基于边划分的并行化方法,该图被划分为三个分区
边划分的优点是可以保留节点的邻居信息,缺点是容易出现划分不均衡,如对于度很高的节点,其关联的边都被分到一个分区中,造成其他分区中的边可能很少。另外,如图5.9中最右边的图所示,边划分可能存在边冗余。
点划分
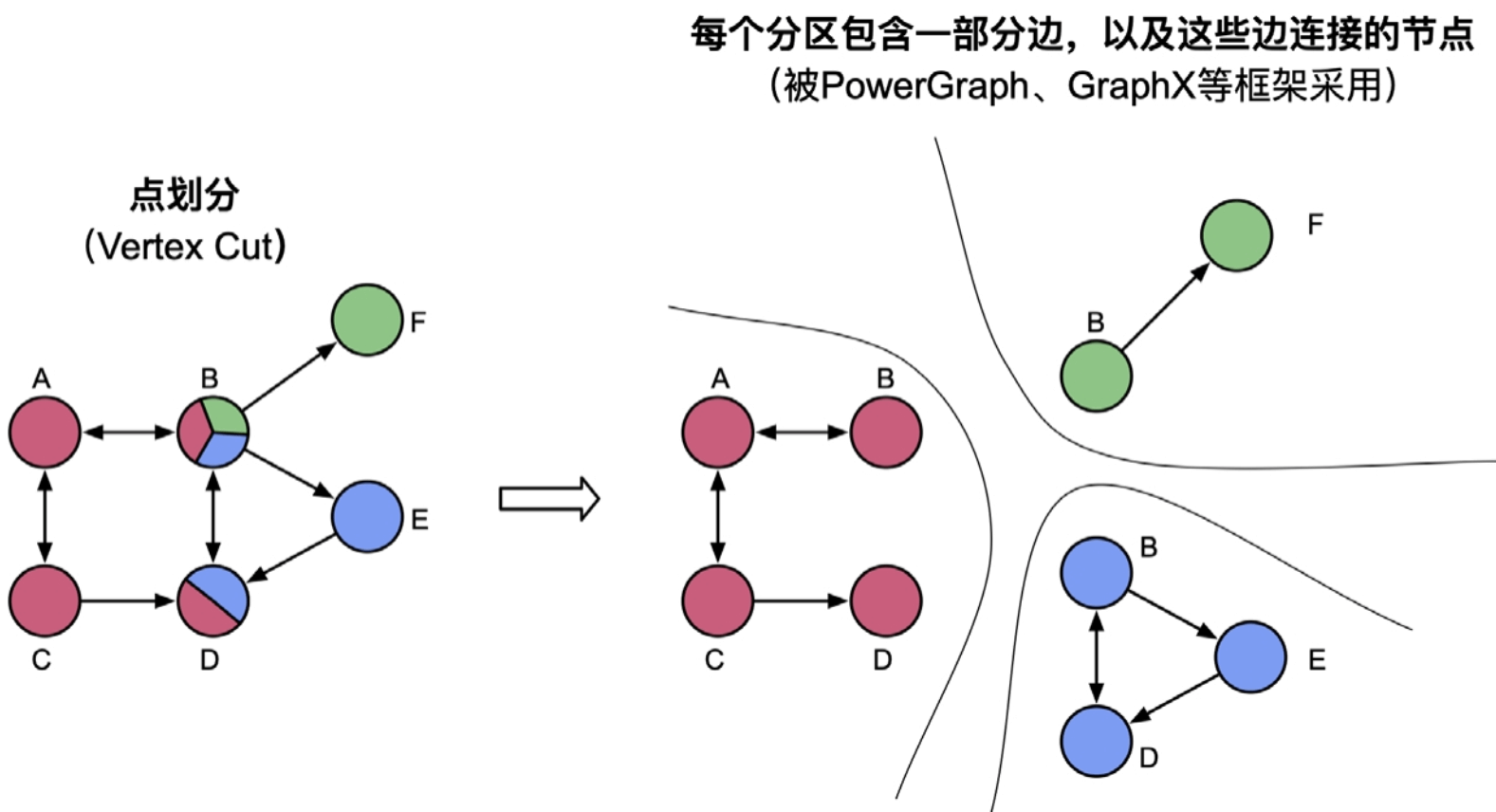
图5.10 基于点划分的并行化方法,该图被划分为三个分区
点划分的优缺点与边划分的优缺点正好相反,可以将边较为平均地分配到不同机器中,但没有保留节点的邻居关系。
总的来说,边划分将节点分布到不同机器中,而点划分将边分布到不同机器中。
下面通过对关键问题进行分析来详细讨论具体的实现流程和原理。
(1)如何对图数据进行表示、存储及访问?
我们知道图的表示方式有多种:邻接矩阵、邻接表、边集合等。邻接矩阵主要在数学运算中使用,如PageRank 计算公式中使用的状态转移矩阵A。直接使用邻接矩阵方式存储图需要O(n2)的存储空间,其中n为图中顶点的个数。这种表示和存储方式的缺点是当图很大时,需要消耗大量存储空间,而且容易出现稀疏问题,即邻接矩阵中大量元素为空。邻接表只存储边信息,可以降低图的存储空间,而且保存了每个顶点的邻居信息。很多图算法,如PageRank,是基于邻居间的消息传播来进行迭代计算的,因此可以选择邻接表来存储图数据。
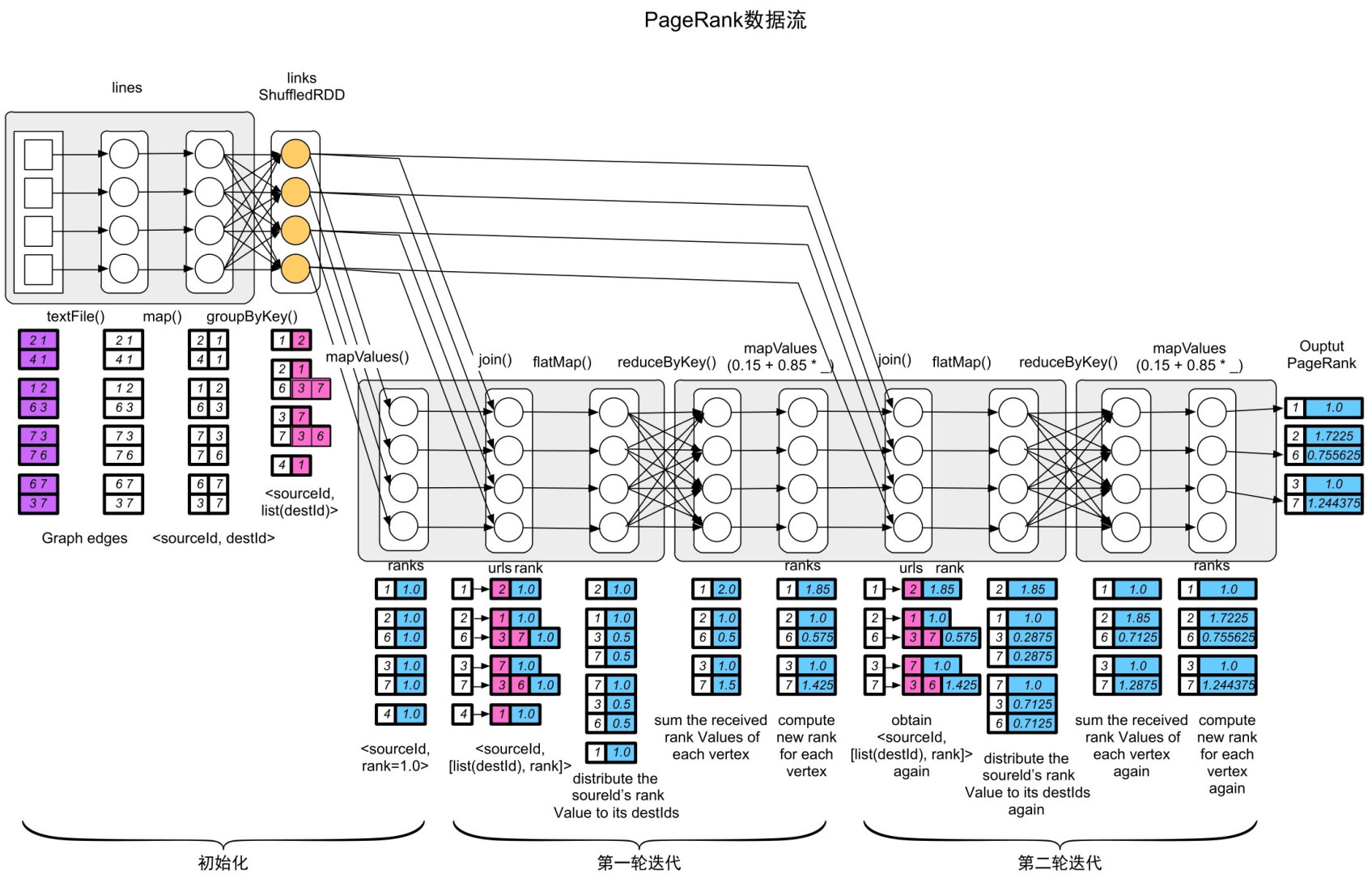
图5.11 SparkPageRank的逻辑处理流程,包含两轮迭代
_
(2)如何对节点的rank值进行初始化?
在迭代计算之前,我们还需要对节点的rank值进行初始化。初始化过程可以分两步执行:第1步是获取输入图中包含的所有节点信息,如图5.11所示,可以执行对邻接表
(3)如何进行迭代计算?
第1步是分发消息,将每个节点的rank值均分到其邻居节点,我们已经有邻接表links:
第2步是收集消息,通过Spark的Shuffle阶段来收集每个节点接收到的邻居消息。具体地,通过reduceByKey(sum)操作,每个节点可以将其收到的rank权重信息聚合在一起,如在图5.11中,节点7收到节点6发来的rank 信息<7,0.5>和节点3发来的rank信息<7,1.0>,经过reduceByKey()后,得到<7,0.5+1.0=1.5>的rank信息,然而这个结果并不是节点7当前的rank值,还需要执行第3步。
第3步是对消息进行聚合计算,在第2步中已经计算了每个节点收到的rank权重之和,我们还需要进一步处理。
之后,不断重复迭代,也就是不断重复以上3个步骤,直至达到最大迭代轮数或收敛(每个节点的rank值变化很小)。本例是简化的PageRank,只使用迭代轮数来控制。
(4)PageRank形成的物理执行计划是什么样的?
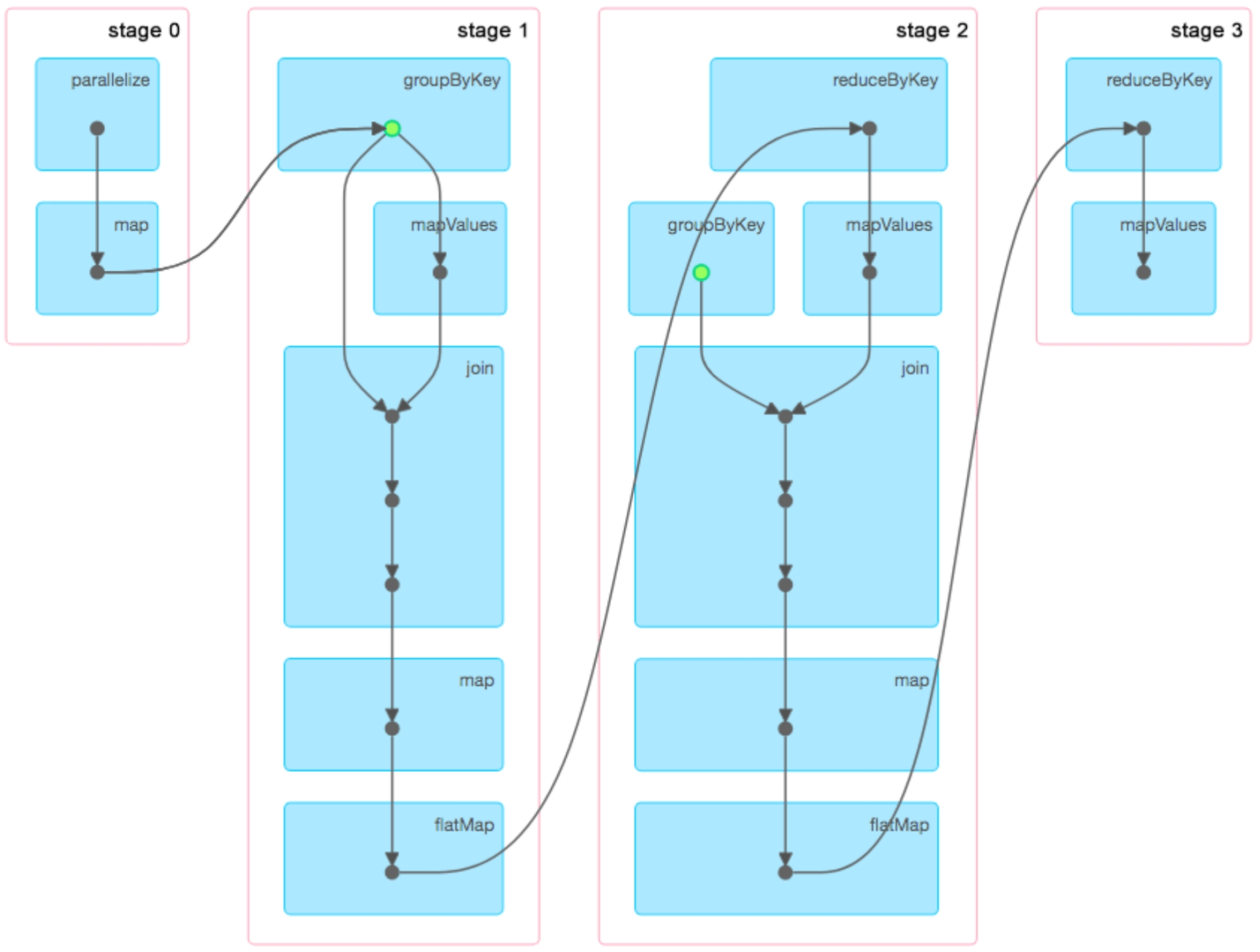
图5.12 SparkPageRank形成的物理执行计划,包含两轮迭代
5.4.3 深入讨论
图计算的编程模型:对于图算法开发者来说,如何将单机的图算法进行并行化以支持大规模图的实现是一个难题。为了解决这个问题,系统研究人员设计了多种编程模型来辅助图算法的并行化实现,包括以顶点为中心(Vertex-Centric)和以边为中心(Edge-Centric)的编程模型等,而最为常用的是以顶点为中心的(Vertex-Centric)编程模型,如PowerGraph系统中采用的Gather-Apply-Scatter (GAS)编程模型等。
我们先回顾一下PageRank在Spark上实现时每轮迭代需要执行的3个步骤:第1步是分发消息(Scatter)阶段,即将节点状态分发给邻居节点;第2步是收集消息(Gather),即通过Shuffle阶段来收集每个节点需要接收到的邻居消息;第3步是对消息进行聚合计算(Apply),根据收到的邻居消息来更新各个节点状态。如果从物理执行计划(stage的角度)来看,如图5.11和图5.12所示,每个stage都执行了3个步骤:收集消息(Gather)→分发消息(Scatter)→对消息进行聚合计算(Apply),这就是GAS模型的计算步骤。当然,在PowerGraph中的GAS模型的具体执行过程要比这个更复杂,采用了异步执行等机制。
如图5.13所示,假设我们将stage命名为超步(superstep),并将stage与stage之间的Shuffle阶段定义为barrier,那么GAS的执行流程符合并行计算领域经典的BulkSynchronous Parallel (BSP)模型,也就是每执行完一个超步(这里是Gather→Apply→Scatter 3个步骤)后同步一次,即所有节点收到邻居节点传播来的消息后,再执行下一个超步。之所以将Shuffle阶段抽象为barrier,是因为Shuffle阶段是stage的分界线,而且只有当上游stage中的所有task完成时才能开始执行下游stage。算法开发人员可以使用Vertex-Centric/GAS编程模型和BSP并行执行模型去实现并行化的图算法,而不用直接去接触MapReduce/Spark的基本操作。
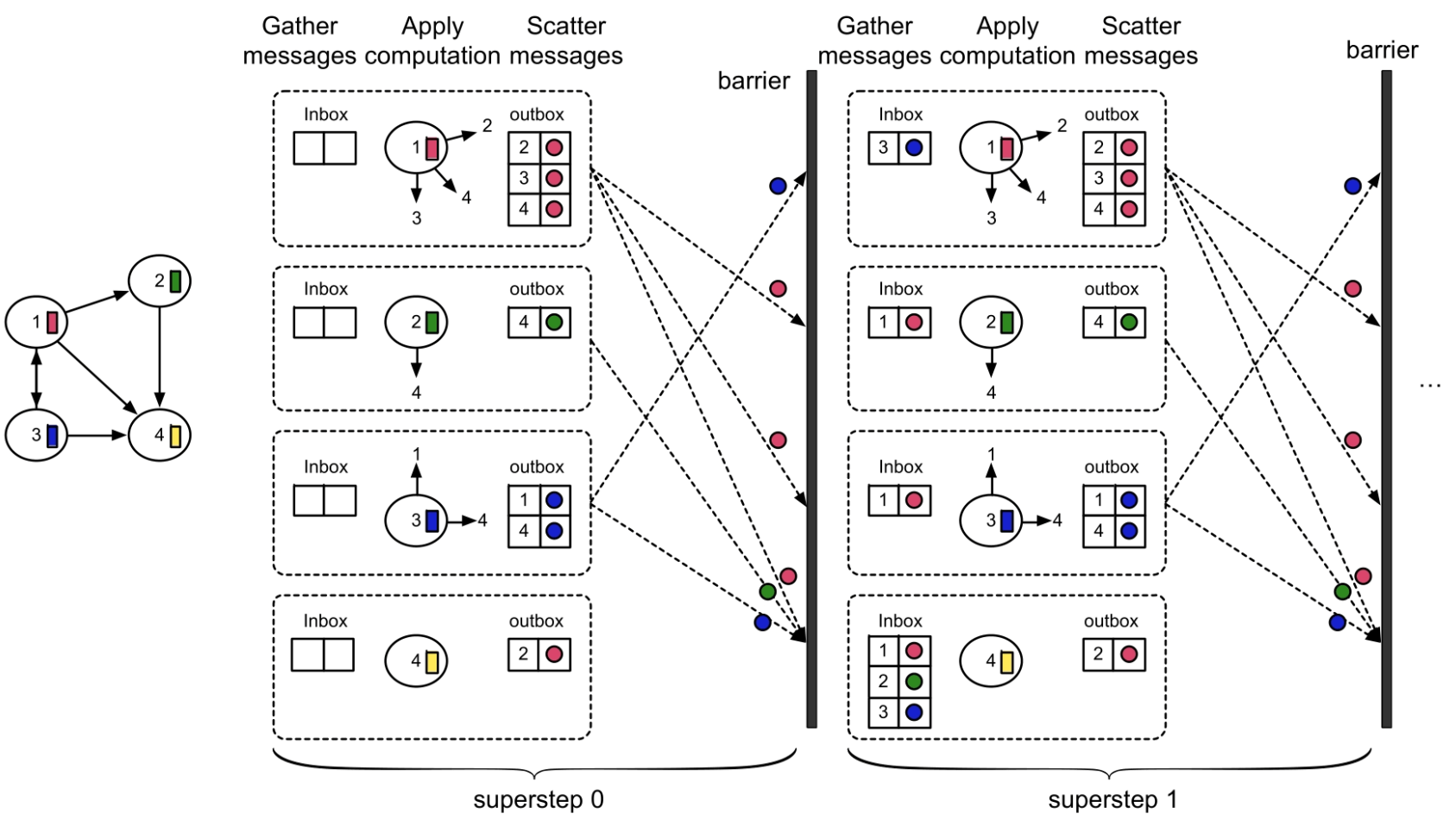
图5.13 以顶点为中心的编程模型

