层次狄利克雷过程（Hierarchical Dirichlet Processes）

提出层次Dirichlet过程的出发点

统计学中，如何将数据分组是一个反复出现的问题。这个问题也就是聚类。传统的聚类方法，如K-Means等都需要人们指定数据中类别的数量，然后模型根据一定的规则求出分组的结果。而Dirichlet过程混合模型（Dirichlet Process Mixture Model， DPMM）则是一种可以自动确定类别数量的聚类方法。与之不同，本文的层次狄利克雷过程模型是另一种分层聚类的模型，它不仅可以自动确定聚类的数量，而且是针对很多组数据建模的。在这个模型中，假设数据是由很多组的，每一组数据都有不知道数量的类别存在。层次狄利克雷模型就是为了找出每一组数据中包含的聚类结果。

首先我们举个例子，在信息检索领域，每个文档都有很多个主题，主题的数量我们不知道。如果只有一个文档，文档中有很多个词语，这些词语都是来自不同的主题，这可以使用DPMM解决。当有了多个文档后，DPMM就只能将它们合成一个大文档进行建模了。而分层狄利克雷模型（Hierarchical Dirichlet Process）可以针对这些不同的文档进行分层建模。
这里要注意与LDA的区别，在LDA模型中，主题的数量是人为确定的，也就是说每个文档下面的词语所属的主题都是来自于这K个主题，但是，当主题数量不知道的时候，使用Dirichlet过程作为先验导致的问题是不同文档下面的相同的主题编号代表了不同的含义。这就无法进行下去了。

我们还是举例来说明。我们是需要解决多组数据的组内聚类问题，因此可以假设对每个小组 j 都有一个与之相关的随机测度的集合 。而 是可以通过与该小组相关的一个Dirichlet过程得到，即。对于不同组的数据聚类，我们可以把不同小组的DP连接起来（意思就是我们为不同的小组数据做组内聚类，而组与组之间的类别可能是相同的，在文档建模中就是每个文档都是一组数据，都有很多个主题组成，我们既要能对每个文档内的主题进行建模，同时也要保证不同文档之间的相同的主题编号代表了同一个主题，所以需要把文档之间连起来）。
有个很简单的思路就能做到这些，就是把不同小组的当做来自于同一个先验的结果，它们都共享一个DP先验，即。但是这里有个问题，当是一个连续分布的时候，尽管我们能通过DP的方式得到的离散的抽样结果，但是这些抽样的结果都不具有相同的原子（atom）。也就是说，尽管组内的数据可以通过DP先验得到一系列的聚类结果，但是组与组之间的聚类标签却是不同的。所以，作者限制了这里的必须是离散的。最简单的做法就是把当做是来自于某个DP先验分布的结果。这样就一定是离散的了。这就是层次狄利克雷过程的基本思想的出发点。

问题描述

首先，我们感兴趣的是具有多个小组的观测值数据。组内的数据与组间的数据都是可交换的。即假设我们用j 表示小组的索引，它是第j 组数据，i 是组内数据点的索引。那么，就是第j 组数据中的数据点。这些数据点都是可交换的。在组级别的数据中，假设表示第j 个小组中的所有的数据，那么也是可交换的。
同时，每个观测点数据都是独立的从一个混合分布中抽取的，也就是说对于每个观测数据来说，都有一个与之相关的混合成分（mixture component）。用表示与观测点相关的混合成分（分布）的参数。我们把称为因子（factors）。注意，这些因子并不一定都是不同的。同时，我们用表示给定因子情况下的分布。假设是第 j 个小组中所有因子的先验分布。我们假设，在给定情况下都是条件独立的，那么，我们有如下的概率模型：

概率图模型

我们根据图1（这个图来自于分层Dirichlet过程及其应用综述）来描述一下J 个文档的生成过程。假设所有文档的主题分布都来自于某个分布H ，那么可以用λ和H作为参数的Dirichlet分布作为先验，在生成某篇文档的时候，我们首先从该先验中抽取一个分布，作为这篇文档的主题分布的先验，然后将和作为参数构造一个Dirichlet分布，抽取一个主题分布作为第 j 篇文档的主题分布，接下来从该主题分布中抽取第 i 个单词的主题，最终从该主题中抽取一个单词。由于所有的文档都共享一个主题分布的先验的参数H，而每个文档主题分布的先验都是从一个以H为基分布的DP中抽取的，因此所有的文档都共享了相同的主题先验了（因为是离散的结果）。

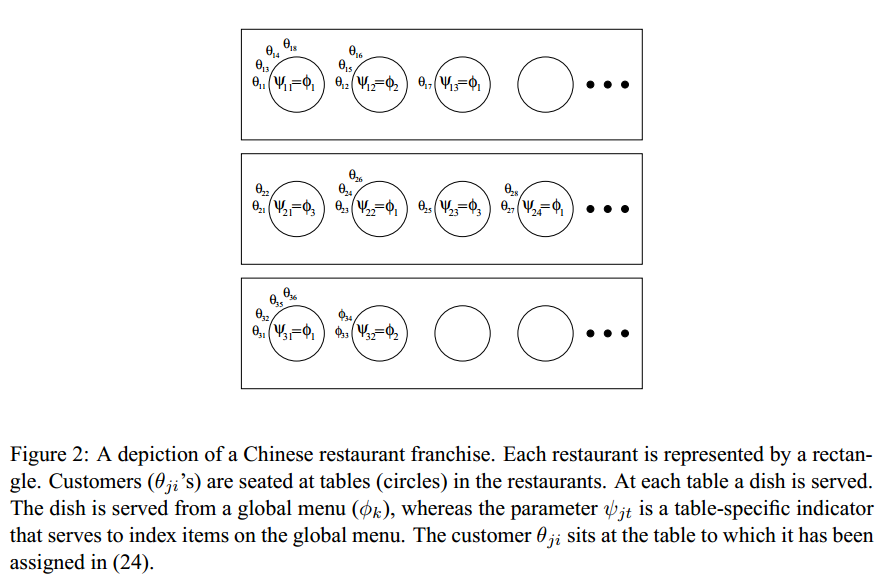
中餐馆特许经营（Chinese Restaurant Franchise）

我们都知道，Dirichlet过程是关于分布的分布，从DP本身的定义中，我们是无法构造一个Dirichlet过程的。层次Dirichlet过程也是一样。这里作者引用了一个叫“中餐馆特许经营”（Chinese Restaurant Franchise，CRF）的构造过程。
假设我们有个有特许经营权的中国餐馆。我们在很多地方都开了这种餐馆，并且他们都拥有相同的菜单。每个特许经验的餐馆中都有无数多的桌子，每个桌子上可以做无数多的人。第一个顾客进来之后选择了一个桌子，并点了一道菜。第二个顾客进来之后既可以选择第一个桌子，也可以选择第二个桌子，这里有一个概率。注意，每个桌子的后来者点的菜都是与坐该桌子第一个顾客点的菜一样，因此，当第二个顾客坐在第一个顾客那张桌子后，菜就不用新点了。而当用户坐在第二张桌子上之后，就要重新点个菜了。这时候，点的菜既可以是和第一张桌子一样，也可以是新的，这也是一个概率选择的问题。不同的桌子可以点到相同的菜，不同餐馆的不同桌子也可能点到相同的菜。一直下去，直到所有的用户落座就结束了。
这里每个餐馆j 都相当于一组数据，每个客户都是一个数据点所属的混合分布的参数，每个桌子都有个指示变量，它对应着一道菜，这道菜就是我们之前理解的文档中的主题了，它就是来自于H 的大家共享的一个参数（注意，这里实际上是来自于H 分布的一个抽样结果，也就是我们之前说的每个数据点来自的分布F 的参数θ，只是一个指示变量，表明每个客户是来自哪个主题ϕ的）。因此，该过程一句话就是顾客i 走进餐馆j ，坐在了桌子边，而餐馆j 中的这个桌子t 对应着一道菜。