习题7.2

习题7.2

  已知正例点，负例点，试求最大间隔分离平面和分类决策函数，并在图中挂出分离超平面、间隔边界及支持向量。

解答：

%matplotlib inline
from sklearn.svm import SVC
# 加载数据
X = [[1, 2], [2, 3], [3, 3], [2, 1], [3, 2]]
y = [1, 1, 1, -1, -1]
# 训练SVM模型
clf = SVC(kernel='linear', C=10000)
clf.fit(X, y)
print("w =", clf.coef_)
print("b =", clf.intercept_)
print("support vectors =", clf.support_vectors_)
w = [[-1.  2.]]
b = [-2.]
support vectors = [[3. 2.]
 [1. 2.]
 [3. 3.]]

最大间隔分离超平面：
分类决策函数：
支持向量：

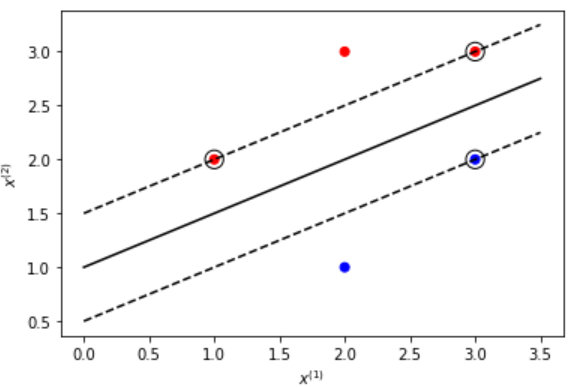
import matplotlib.pyplot as plt
import numpy as np
# 绘制数据点
color_seq = ['red' if v == 1 else 'blue' for v in y]
plt.scatter([i[0] for i in X], [i[1] for i in X], c=color_seq)
# 得到x轴的所有点
xaxis = np.linspace(0, 3.5)
w = clf.coef_[0]
# 计算斜率
a = -w[0] / w[1]
# 得到分离超平面
y_sep = a * xaxis - (clf.intercept_[0]) / w[1]
# 下边界超平面
b = clf.support_vectors_[0]
yy_down = a * xaxis + (b[1] - a * b[0])
# 上边界超平面
b = clf.support_vectors_[-1]
yy_up = a * xaxis + (b[1] - a * b[0])
# 绘制超平面
plt.plot(xaxis, y_sep, 'k-')
plt.plot(xaxis, yy_down, 'k--')
plt.plot(xaxis, yy_up, 'k--')
# 绘制支持向量
plt.xlabel('$x^{(1)}$')
plt.ylabel('$x^{(2)}$')
plt.scatter(clf.support_vectors_[:, 0],
            clf.support_vectors_[:, 1],
            s=150,
            facecolors='none',
            edgecolors='k')
plt.show()