参照图3.1，在二维空间中给出实例点，画出k为1和2时的k近邻法构成的空间划分，并对其进行比较，体会k值选择与模型复杂度及预测准确率的关系。

    解：

    1. import numpy as np
    2. import matplotlib.pyplot as plt
    3. from matplotlib.colors import ListedColormap
    4. from sklearn.neighbors import KNeighborsClassifier
    6. # 实例点
    7. x = np.array(
    8.     [[0.5, 0.9], [0.7, 2.8], [1.3, 4.6], [1.4, 2.8], [1.7, 0.8], [1.9, 1.4], [2, 4], [2.3, 3], [2.5, 2.5], [2.9, 2],
    9.      [2.9, 3], [3, 4.5], [3.3, 1.1], [4, 3.7], [4, 2.2], [4.5, 2.5], [4.6, 1], [5, 4]])
    11. # 类别
    12. y = np.array([0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0])
    14. # 设置二维网格的边界
    15. x_min, x_max = 0, 6
    16. y_min, y_max = 0, 6
    18. # 设置不同类别区域的颜色
    19. cmap_light = ListedColormap(['#FFFFFF', '#BDBDBD'])
    21. # 生成二维网格
    22. h = .01
    23. xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    25. # 这里的参数n_neighbors就是k近邻法中的k
    26. knn = KNeighborsClassifier(n_neighbors=2)
    27. knn.fit(x, y)
    29. # ravel()实现扁平化，比如将形状为3*4的数组变成1*12
    30. # np.c_()在列方向上连接数组，要求被连接数组的行数相同
    31. Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
    32. Z = Z.reshape(xx.shape)
    34. plt.figure()
    36. # 设置坐标轴的刻度
    37. plt.xticks(tuple([x for x in range(6)]))
    38. plt.yticks(tuple([y for y in range(6) if y != 0]))
    40. # 填充不同分类区域的颜色
    41. plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
    43. # 设置坐标轴标签
    44. plt.xlabel('$x^{(1)}$')
    45. plt.ylabel('$x^{(2)}$')
    47. # 绘制实例点的散点图
    48. plt.scatter(x[:, 0], x[:, 1], c=y)
    50. plt.show()

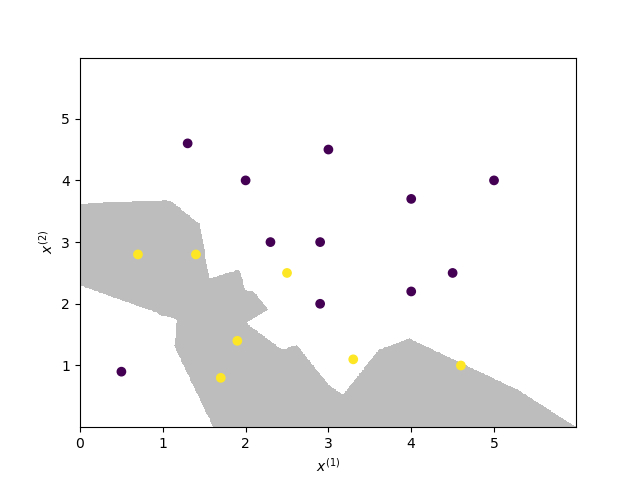
    k=1时的KNN算法构成的空间划分：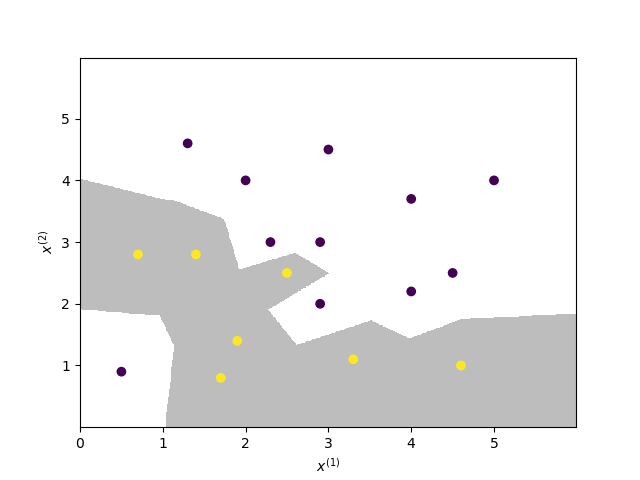
    Figure_1.png
    k=2时的KNN算法构成的空间划分：
    Figure_2.png