习题7.1

习题7.1

  比较感知机的对偶形式与线性可分支持向景机的对偶形式。

解答：

感知机算法的原始形式：

给定一个训练数据集

其中，，求参数，使其为以下损失函数极小化问题的解：

其中M为误分类点的集合。
上式等价于：

补充： 合页损失函数

下标“+”表示以下取正数的函数。

当样本点被正确分类且函数间隔（确信度）大于1时，损失是0，否则损失是。

感知机算法的对偶形式：

![](https://cdn.nlark.com/yuque/0/2020/svg/1061864/1602060887349-1f9da4d0-9d98-4c5d-ade6-79b58df8c7ac.svg#align=left&display=inline&height=13&margin=%5Bobject%20Object%5D&originHeight=13&originWidth=30&size=0&status=done&style=none&width=30)表示为![](https://cdn.nlark.com/yuque/0/2020/svg/1061864/1602060887734-58c6ab88-437c-4032-bec9-25c4bea193b8.svg#align=left&display=inline&height=29&margin=%5Bobject%20Object%5D&originHeight=29&originWidth=52&size=0&status=done&style=none&width=52)的线性组合的形式，求其系数（线性组合的系数）![](https://cdn.nlark.com/yuque/0/2020/svg/1061864/1602060884926-eea52dc8-8d53-4328-a02f-2415e1309e68.svg#align=left&display=inline&height=47&margin=%5Bobject%20Object%5D&originHeight=47&originWidth=192&size=0&status=done&style=none&width=192)，满足：<br />![](https://cdn.nlark.com/yuque/0/2020/svg/1061864/1602060885262-e9ba115b-be65-4e61-92fb-c5f1edd7fefe.svg#align=left&display=inline&height=23&margin=%5Bobject%20Object%5D&originHeight=23&originWidth=528&size=0&status=done&style=none&width=528)

线性可分支持向量机的原始问题：

线性可分支持向量机的对偶问题：

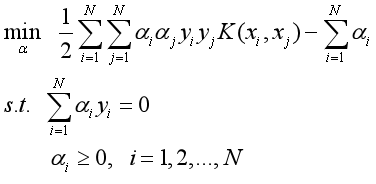
根据书上定理7.2，可得，可以看出实质上也是将其表示为的线性组合形式。