5.1

根据表5.1所给的训练数据集，利用信息增益比（C4.5算法）生成决策树.

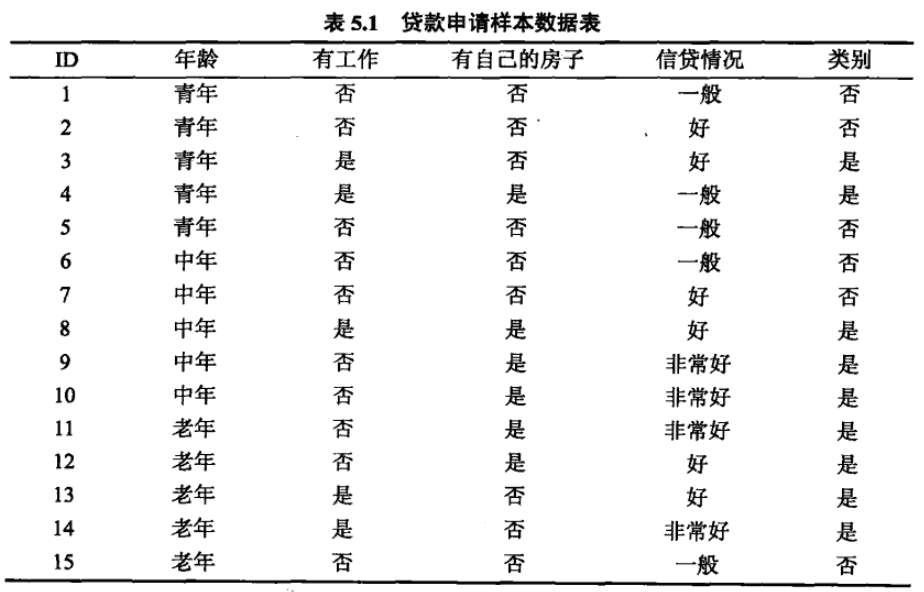
image.png
先计算每个特征的信息增益比，信息增益比第五章习题 - 图2。
其中D关于特征A的熵第五章习题 - 图3（n为A特征的取值个数）
D关于特征A的条件熵
信息增益 第五章习题 - 图4
分别以第五章习题 - 图5表示年龄、有工作、有自己的房子和信贷情况4个特征。
经验熵第五章习题 - 图6：
第五章习题 - 图7
第五章习题 - 图8
第五章习题 - 图9
第五章习题 - 图10

例题5.2已经计算了各个特征的信息增益：
第五章习题 - 图11 第五章习题 - 图12 第五章习题 - 图13 第五章习题 - 图14

得信息增益比：
第五章习题 - 图15 第五章习题 - 图16 第五章习题 - 图17 第五章习题 - 图18

选择信息增益比最大的特征第五章习题 - 图19作为根节点特征，将训练集分为两个子集第五章习题 - 图20和第五章习题 - 图21，由于第五章习题 - 图22中只有同一类样本点，所以它是一个叶节点，标记为“是”,对第五章习题 - 图23从第五章习题 - 图24中选择新的特征，第五章习题 - 图25中的元素有：

第五章习题 - 图26
重新计算各个特征的信息增益比
经验熵：
第五章习题 - 图27

信息增益：
第五章习题 - 图28
其中第五章习题 - 图29分别表示第五章习题 - 图30中第五章习题 - 图31取值为青年，中年，老年的样本子集。

第五章习题 - 图32
其中第五章习题 - 图33分别表示第五章习题 - 图34中第五章习题 - 图35取值为否，是的样本子集。

第五章习题 - 图36
其中第五章习题 - 图37分别表示第五章习题 - 图38中第五章习题 - 图39取值为一般，好，非常好的样本子集。

信息增益比：
第五章习题 - 图40

第五章习题 - 图41

第五章习题 - 图42
选择信息增益比最大的特征第五章习题 - 图43作为节点的特征，从这一结点引出两个子结点：一个对应“是”（有工作）的子结点，包含3个样本，它们属于同一类，所以这是一个叶结点，类标记为“是”；另一个是对应“否”（无工作）的子结点，包含6个样本，它们也属于同一类，所以这也是一个叶结点，类标记为“否”。
最终的决策树如图：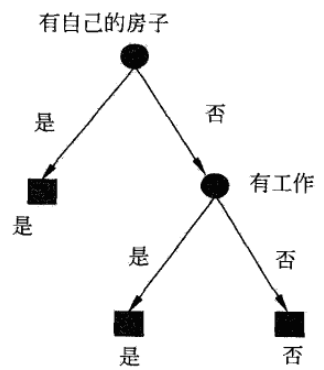
image.png

代码：

例题5.3用ID3算法生成决策树（信息增益）

  1. import numpy as np
  2. from math import log
  4. def loadData():
  5.     datasets = [['青年', '否', '否', '一般', '否'],
  6.                ['青年', '否', '否', '好', '否'],
  7.                ['青年', '是', '否', '好', '是'],
  8.                ['青年', '是', '是', '一般', '是'],
  9.                ['青年', '否', '否', '一般', '否'],
  10.                ['中年', '否', '否', '一般', '否'],
  11.                ['中年', '否', '否', '好', '否'],
  12.                ['中年', '是', '是', '好', '是'],
  13.                ['中年', '否', '是', '非常好', '是'],
  14.                ['中年', '否', '是', '非常好', '是'],
  15.                ['老年', '否', '是', '非常好', '是'],
  16.                ['老年', '否', '是', '好', '是'],
  17.                ['老年', '是', '否', '好', '是'],
  18.                ['老年', '是', '否', '非常好', '是'],
  19.                ['老年', '否', '否', '一般', '否'],
  20.                ]
  21.     labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']
  22.     # 返回数据集和每个维度的名称
  23.     return datasets, labels
  25. # 计算熵
  26. def calc_entropy(datasets):
  27.     label_count = {}
  28.     for dataset in datasets:
  29.         label =  dataset[-1]
  30.         if label not in label_count:
  31.             label_count[label] = 0
  32.         label_count[label] += 1
  33.     entropy = -sum([(p/len(datasets))*log(p/len(datasets),2) for p in label_count.values()])
  34.     return entropy
  36. # 计算条件熵
  37. def calc_conditional_entropy(datasets, index = 0):
  38.     feature_data = {}
  39.     for dataset in datasets:
  40.         feature = dataset[index]
  41.         if feature not in feature_data:
  42.             feature_data[feature] = []
  43.         feature_data[feature].append(dataset)
  44.     condEntropy = sum([(len(p)/len(datasets))*calc_entropy(p) for p in feature_data.values()])
  45.     return condEntropy
  47. # 计算信息增益
  48. def info_gain(entropy, condEntropy):
  49.     return entropy - condEntropy
  51. def info_gain_train_childTree(datasets, labels):
  52.     entropy = calc_entropy(datasets)
  53.     features = []
  54.     for index in range(len(datasets[0])-1):
  55.         condEntropy = calc_conditional_entropy(datasets, index)
  56.         c_info_gain = info_gain(entropy, condEntropy)
  57.         features.append((index, c_info_gain))
  58.         print("特征({})的信息增益为{:.3f}".format(labels[index], c_info_gain))
  59.     best_feature = max(features, key=lambda x: x[-1])
  60.     print("特征({})的信息增益最大，选择为当前节点特征".format(labels[best_feature[0]]))
  61.     return best_feature
  63. def info_gain_train(datasets, labels):
  64.     label_count = {}
  65.     for dataset in datasets:
  66.         label = dataset[-1]
  67.         if label not in label_count:
  68.             label_count[label] = 0
  69.         label_count[label] += 1
  70.     if len(label_count.keys()) == 1:
  71.         key = list(label_count.keys())[0]
  72.         print("此时类别均为{}".format(key))
  73.         return
  74.     best_feature = info_gain_train_childTree(datasets, labels)
  76.     feature_data = {}
  77.     for dataset in datasets:
  78.         feature = dataset[best_feature[0]]
  79.         if feature not in feature_data:
  80.             feature_data[feature] = []
  81.         feature_data[feature].append(dataset)
  83.     for data in zip(feature_data.keys(), feature_data.values()):
  84.         print("当{}为{}".format(labels[best_feature[0]], data[0]))
  85.         info_gain_train(data[1], labels)
  88. if __name__ == "__main__":
  89.     datasets, labels = loadData()
  90.     info_gain_train(datasets, labels)

运行结果：

  1. 特征(年龄)的信息增益为0.083
  2. 特征(有工作)的信息增益为0.324
  3. 特征(有自己的房子)的信息增益为0.420
  4. 特征(信贷情况)的信息增益为0.363
  5. 特征(有自己的房子)的信息增益最大，选择为当前节点特征
  6. 当有自己的房子为否
  7. 特征(年龄)的信息增益为0.252
  8. 特征(有工作)的信息增益为0.918
  9. 特征(有自己的房子)的信息增益为0.000
  10. 特征(信贷情况)的信息增益为0.474
  11. 特征(有工作)的信息增益最大，选择为当前节点特征
  12. 当有工作为否
  13. 此时类别均为否
  14. 当有工作为是
  15. 此时类别均为是
  16. 当有自己的房子为是
  17. 此时类别均为是

C4.5生成算法（信息增益比）

  1. import numpy as np
  2. from math import log
  4. def loadData():
  5.     datasets = [['青年', '否', '否', '一般', '否'],
  6.                ['青年', '否', '否', '好', '否'],
  7.                ['青年', '是', '否', '好', '是'],
  8.                ['青年', '是', '是', '一般', '是'],
  9.                ['青年', '否', '否', '一般', '否'],
  10.                ['中年', '否', '否', '一般', '否'],
  11.                ['中年', '否', '否', '好', '否'],
  12.                ['中年', '是', '是', '好', '是'],
  13.                ['中年', '否', '是', '非常好', '是'],
  14.                ['中年', '否', '是', '非常好', '是'],
  15.                ['老年', '否', '是', '非常好', '是'],
  16.                ['老年', '否', '是', '好', '是'],
  17.                ['老年', '是', '否', '好', '是'],
  18.                ['老年', '是', '否', '非常好', '是'],
  19.                ['老年', '否', '否', '一般', '否'],
  20.                ]
  21.     labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']
  22.     # 返回数据集和每个维度的名称
  23.     return datasets, labels
  25. def calc_entropy(datasets, index=-1):
  26.     label_count = {}
  27.     for dataset in datasets:
  28.         label =  dataset[index]
  29.         if label not in label_count:
  30.             label_count[label] = 0
  31.         label_count[label] += 1
  32.     entropy = -sum([(p/len(datasets))*log(p/len(datasets),2) for p in label_count.values()])
  33.     return entropy
  35. def calc_conditional_entropy(datasets, index = 0):
  36.     feature_data = {}
  37.     for dataset in datasets:
  38.         feature = dataset[index]
  39.         if feature not in feature_data:
  40.             feature_data[feature] = []
  41.         feature_data[feature].append(dataset)
  42.     condEntropy = sum([(len(p)/len(datasets))*calc_entropy(p) for p in feature_data.values()])
  43.     return condEntropy
  45. def info_gain(entropy, condEntropy):
  46.     return entropy - condEntropy
  48. def info_gain_ratio(c_info_gain, c_entropy):
  49.     return 0 if c_info_gain == 0 else c_info_gain / c_entropy
  51. def info_gain_train_childTree(datasets, labels):
  52.     entropy = calc_entropy(datasets)
  53.     features = []
  54.     for index in range(len(datasets[0])-1):
  55.         condEntropy = calc_conditional_entropy(datasets, index)
  56.         c_info_gain = info_gain(entropy, condEntropy)
  57.         c_entropy = calc_entropy(datasets, index)
  58.         c_info_gain_ratio = info_gain_ratio(c_info_gain, c_entropy)
  59.         features.append((index, c_info_gain_ratio))
  60.         print("特征({})的信息增益比为{:.3f}".format(labels[index], c_info_gain_ratio))
  61.     best_feature = max(features, key=lambda x: x[-1])
  62.     print("特征({})的信息增益比最大，选择为当前节点特征".format(labels[best_feature[0]]))
  63.     return best_feature
  65. def info_gain_train(datasets, labels):
  66.     label_count = {}
  67.     for dataset in datasets:
  68.         label = dataset[-1]
  69.         if label not in label_count:
  70.             label_count[label] = 0
  71.         label_count[label] += 1
  72.     if len(label_count.keys()) == 1:
  73.         key = list(label_count.keys())[0]
  74.         print("此时类别均为{}".format(key))
  75.         return
  76.     best_feature = info_gain_train_childTree(datasets, labels)
  78.     feature_data = {}
  79.     for dataset in datasets:
  80.         feature = dataset[best_feature[0]]
  81.         if feature not in feature_data:
  82.             feature_data[feature] = []
  83.         feature_data[feature].append(dataset)
  85.     for data in zip(feature_data.keys(), feature_data.values()):
  86.         print("当{}为{}".format(labels[best_feature[0]], data[0]))
  87.         info_gain_train(data[1], labels)
  90. if __name__ == "__main__":
  91.     datasets, labels = loadData()
  92.     info_gain_train(datasets, labels)

运行结果：

  1. 特征(年龄)的信息增益比为0.052
  2. 特征(有工作)的信息增益比为0.352
  3. 特征(有自己的房子)的信息增益比为0.433
  4. 特征(信贷情况)的信息增益比为0.232
  5. 特征(有自己的房子)的信息增益比最大，选择为当前节点特征
  6. 当有自己的房子为否
  7. 特征(年龄)的信息增益比为0.164
  8. 特征(有工作)的信息增益比为1.000
  9. 特征(有自己的房子)的信息增益比为0.000
  10. 特征(信贷情况)的信息增益比为0.340
  11. 特征(有工作)的信息增益比最大，选择为当前节点特征
  12. 当有工作为否
  13. 此时类别均为否
  14. 当有工作为是
  15. 此时类别均为是
  16. 当有自己的房子为是
  17. 此时类别均为是

5.2

已知下表所示的训练数据，试用平方误差损失准则生成一个二叉回归树.

x__i 1 2 3 4 5 6 7 8 9 10
y__i 4.50 4.75 4.91 5.34 5.80 7.05 7.70 8.23 8.70 9.00

回归树的建立算法：
image.png

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  4. #节点定义
  5. class TreeNode(object):
  6.     def __init__(self, tempR, tempc):
  7.         self.R = tempR
  8.         self.c = tempc
  9.         self.left = None
  10.         self.right = None
  12. # y的值
  13. y = np.array([4.5, 4.75, 4.91, 5.34, 5.8, 7.05, 7.9, 8.23, 8.7, 9]) 
  15. #CART算法建立回归树
  16. def CART(start, end):
  17.     # 切点s的选择表示R1为x值小于等于s的点，R2为大于s的点
  18.     if(end - start >= 1):
  19.         result = []
  20.         for s in range(start+1, end+1):  # s在(start, end]之间取值
  21.             y1 = y[start : s]   # y1取索引为[start, s]之间的值
  22.             y2 = y[s: end+1]    # y2取索引为[s+1, end]之间的值
  23.             result.append((y1.std()**2)*y1.size + (y2.std()**2)*y2.size)
  24.             # std即标准差函数，求标准差的时候默认除以元素的个数，因此平方后乘以元素个数才是要求的平方差
  25.         index1 = result.index(min(result)) + start # 取平方差误差最小的索引值
  26.         root = TreeNode(y[start:end+1], min(result))
  27.         # 索引值为0-9，x值为1-10，即s的值比求的索引值多1
  28.         print("节点元素值为",y[start:end+1], "  s =",index1+1, "  最小平方误差为",min(result))#输出s值和最小平方误差
  29.         root.left = CART(start, index1)   # 对列表的左侧生成左子树
  30.         root.right = CART(index1+1, end)  # 对列表的右侧生成右子树
  31.     else:
  32.         root = None
  33.     return root
  36. if __name__ == "__main__":
  37.     root = CART(0, 9)

运行结果：

  1. 节点元素值为 [4.5  4.75 4.91 5.34 5.8  7.05 7.9  8.23 8.7  9.  ]   s = 5   最小平方误差为 3.3587199999999986
  2. 节点元素值为 [4.5  4.75 4.91 5.34 5.8 ]   s = 3   最小平方误差为 0.1912
  3. 节点元素值为 [4.5  4.75 4.91]   s = 1   最小平方误差为 0.012800000000000023
  4. 节点元素值为 [4.75 4.91]   s = 2   最小平方误差为 0.0
  5. 节点元素值为 [5.34 5.8 ]   s = 4   最小平方误差为 0.0
  6. 节点元素值为 [7.05 7.9  8.23 8.7  9.  ]   s = 7   最小平方误差为 0.6625166666666665
  7. 节点元素值为 [7.05 7.9 ]   s = 6   最小平方误差为 0.0
  8. 节点元素值为 [8.23 8.7  9.  ]   s = 8   最小平方误差为 0.04500000000000021
  9. 节点元素值为 [8.7 9. ]   s = 9   最小平方误差为 0.0

计算过程：
以根节点为例，变换切分点s，选择使得平方误差最小的切分点
s=1:
即第五章习题 - 图46
此时有第五章习题 - 图47，第五章习题 - 图48
然后依次将s从2取值到10，计算平方误差，选其中平方误差最小的s为根节点s，将元素分为左右子树后，再对左右子树进行相同的处理。