一、算法概念
1. 介绍
算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。
算法中的指令描述的是一个计算,当其运行时能从一个初始状态和(可能为空的)初始输入开始,经过一系列有限而清晰定义的状态,最终产生输出并停止于一个终态。一个状态到另一个状态的转移不一定是确定的。随机化算法在内的一些算法,包含了一些随机输入。
2. 特征
- 输入:一个算法必须有零个或以上输入量。
- 输出:一个算法应有一个或以上输出量,输出量是算法计算的结果。
- 明确性:算法的描述必须无歧义,以保证算法的实际执行结果是精确地符合要求或期望,通常要求实际执行结果是确定的。
- 有限性:依据图灵的定义,一个演算法是能够被任何图灵完备系统模拟的一串运算,而图灵机只有有限个状态、有限个输入符号和有限个转移函数(指令)。而一些定义更规定演算法必须在有限个步骤内完成任务。
- 有效性:又称可行性。能够实现,算法中描述的操作都是可以通过已经实现的基本运算执行有限次来实现。
3. 如何测算算法的优劣
1. 时间测算
- 计算算法时间差
- 幅度不够循环来凑(使不同算法之间的时间差更加明显)
2. 空间测算
3. 常数项时间(实现细节决定)
4. 如何编写算法
- 由简单到复杂
- 验证一步走一步
- 多打印中间结果
- 先局部后整体
- 没思路时先细分
- 先粗糙后精细
- 变量更名
- 语句合并
- 边界处理
4. 复杂度(Big O)
时间——问题(数据)的规模
- 不考虑必须要做的操作:循环、赋初值、程序初始化
- 不考虑常数项:2n —> n
- 不考虑低次项:n平方+n —> n平方
1. 时间复杂度
在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况
为了计算时间复杂度,我们通常会估计算法的操作单元数量,每个单元运行的时间都是相同的。因此,总运行时间和算法的操作单元数量最多相差一个常量系数。
相同大小的不同输入值仍可能造成算法的运行时间不同,因此我们通常使用算法的最坏情况复杂度,记为T(n),定义为任何大小的输入n所需的最大运行时间。另一种较少使用的方法是平均情况复杂度,通常有特别指定才会使用。时间复杂度可以用函数T(n) 的自然特性加以分类,举例来说,有着T(n) =O(n) 的算法被称作“线性时间算法”;而T(n) =O(M^n) 和M= O(T(n)) ,其中M≥n> 1 的算法被称作“指数时间算法”
对数与指数
2. 空间复杂度
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度,记做S(n)=O(f(n))。比如直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度了,因为每次递归都要存储返回信息。一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量
类似于时间复杂度的讨论,一个算法的空间复杂度S(n)定义为该算法所耗费的存储空间,它也是问题规模n的函数。渐近空间复杂度也常常简称为空间复杂度。空间复杂度(SpaceComplexity)是对一个算法在运行过程中临时占用存储空间大小的量度
一个算法在计算机存储器上所占用的存储空间,包括存储算法本身所占用的存储空间,算法的输入输出数据所占用的存储空间和算法在运行过程中临时占用的存储空间这三个方面。算法的输入输出数据所占用的存储空间是由要解决的问题决定的,是通过参数表由调用函数传递而来的,它不随本算法的不同而改变。
二、排序算法
1. 选择排序
如何验证算法是否正确
- 肉眼观察
- 产生足够多的随机样本
- 用确定正确的算法计算样本结果
- 对比被验证算法的结果
对数器
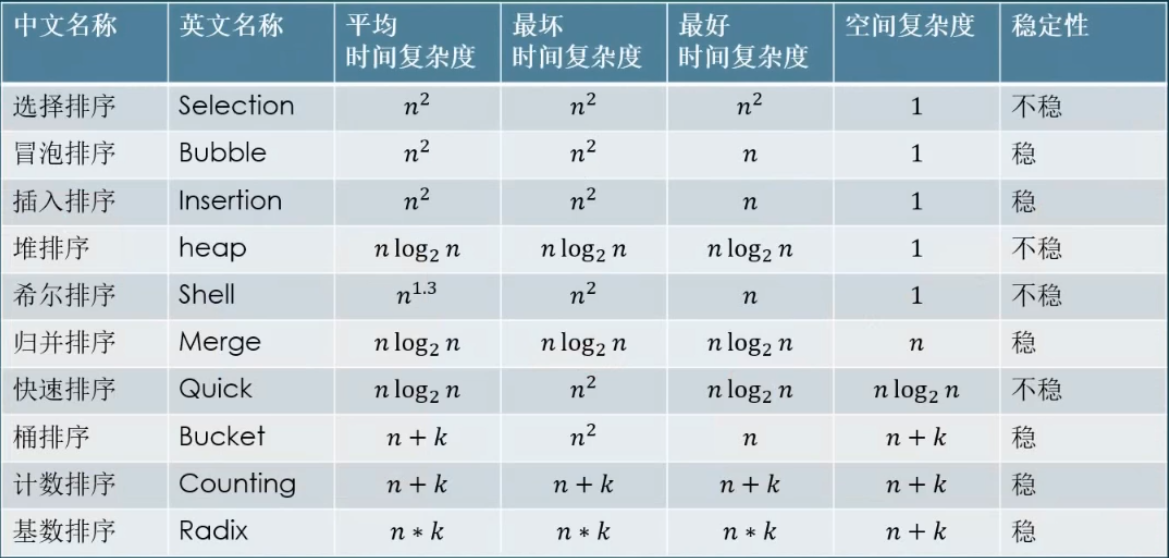
2. 排序算法总结
- 不基于比较的排序,对样本数据有严格要求,不易改写(基数、计数、桶)
- 基于比较的排序,只要规定好两个样本是怎么比较的就可以直接复用
- 基于比较的排序,时间复杂度的极限是O(N*logN)
- 时间复杂度O(N*logN),额外空间复杂度低于O(N),且稳定的基于比较的排序是不存在的
- 为了绝对的速度选择快排,为了节省空间选择堆排,为了稳定选择归并
常见的坑
- 归并排序的额外空间复杂度可以变为O(1),“归并排序内部缓存法”但是将不再稳定
- “原地归并排序”是垃圾贴,会让时间复杂度变为O(N^2)
- 快速排序稳定性改进,“01 stable sort”但是会对样本数据要求更多
3. JAVA底层对排序的优化
Java底层对排序算法做了大量复杂优化

