快速排序

数组和链表

• 计算机内存犹如一大堆抽屉。
• 需要存储多个元素时，可使用数组或链表。
• 数组的元素都在一起。
• 链表的元素是分开的，其中每个元素都存储了下一个元素的地址。
• 数组的读取速度很快。
• 链表的插入和删除速度很快。
• 在同一个数组中，所有元素的类型都必须相同（都为int、double等）。

分而治之

分而治之 （divide and conquer，D&C）——一种著名的递归式问题解决方法。

D&C的工作原理：

1. 找出简单的基线条件；
2. 确定如何缩小问题的规模，使其符合基线条件。
   D&C并非可用于解决问题的算法，而是一种解决问题的思路

提示

编写涉及数组的递归函数时，基线条件通常是数组为空或只包含一个元素。陷入困境时，请检查基线条件是不是这样的。

快速排序

分析工作原理

1. 根本不需要排序的数组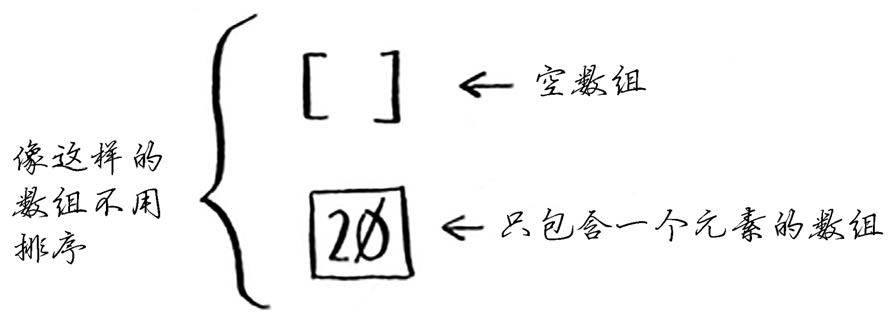

基线条件为数组为空或只包含一个元素

def quicksort(array):
   if len(array) < 2:
       return array

2. 两个元素的数组进行排序

3. 三个元素排序
使用D&C，因此需要将数组分解，直到满足基线条件。
首先，从数组中选择一个元素，这个元素被称为基准值（pivot）。

暂时将数组的第一个元素用作基准值，接下来，找出比基准值小的元素以及比基准值大的元素。

这被称为分区（partitioning）。现在你有：

• 一个由所有小于基准值的数字组成的子数组；
• 基准值；
• 一个由所有大于基准值的数组组成的子数组。

然后对子数组再进行排序

quicksort([15, 10]) + [33] + quicksort([]) > [10, 15, 33] 一个有序数组

三个元素的数组进行排序了，步骤如下。

1. 选择基准值。
2. 将数组分成两个子数组：小于基准值的元素和大于基准值的元素。
3. 对这两个子数组进行快速排序。

下面是快速排序的代码

平均情况和最糟情况

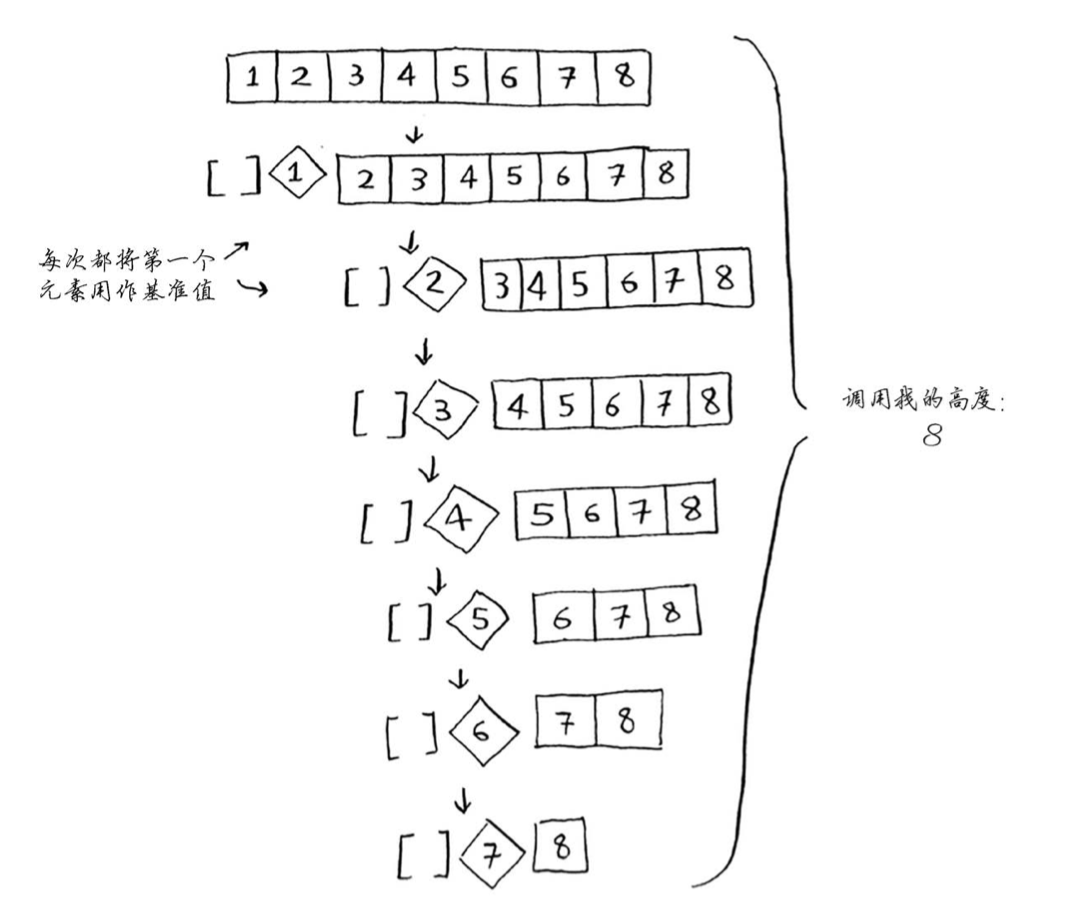
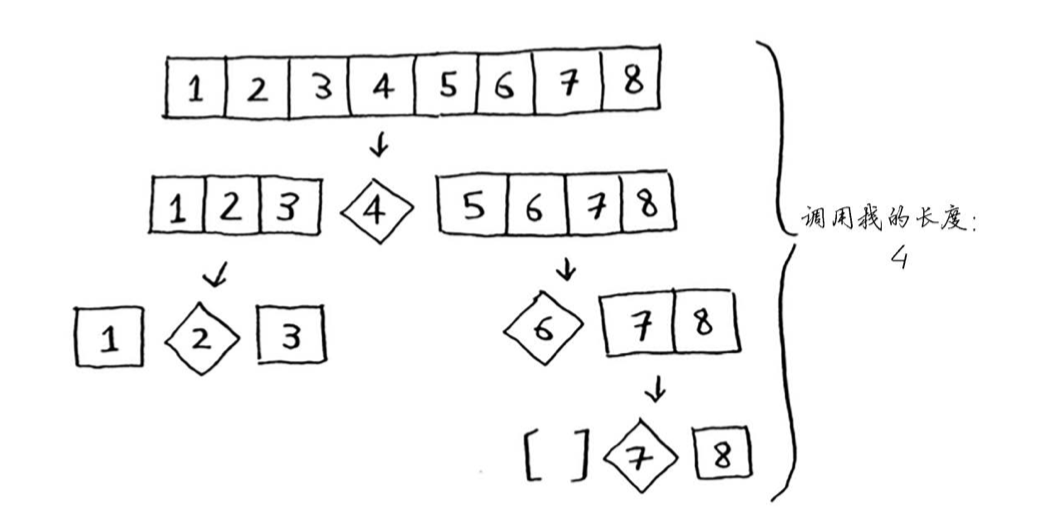
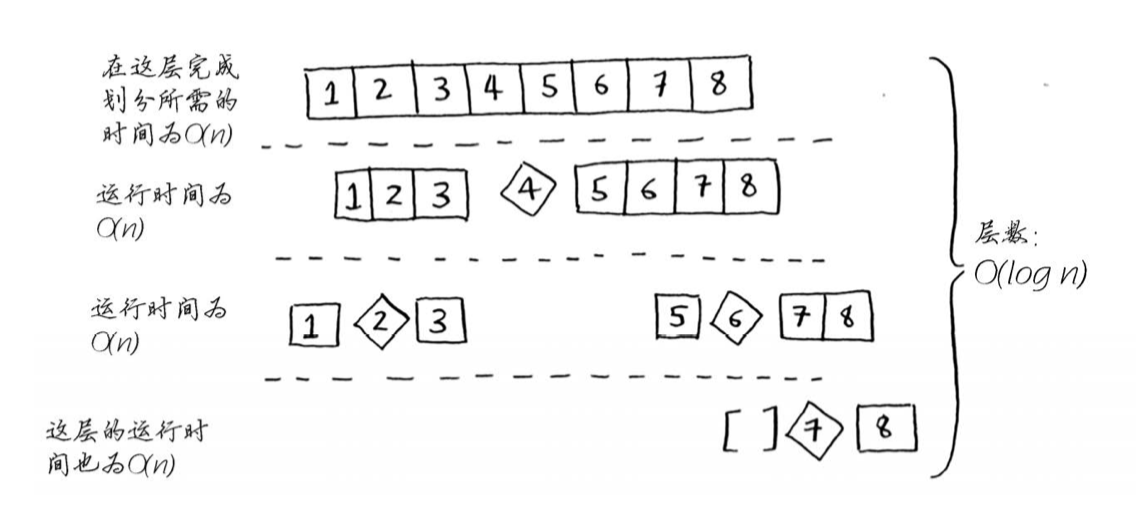
完成每层所需的时间都为O(n)

• 最佳情况：层数为（用技术术语说，调用栈的高度为O(log n)），时间为。
• 最糟情况：运行时间为。

最佳情况也是平均情况。只要你每次都随机地选择一个数组元素作为基准值，快速排序的平均运行时间就将为O(n log n)。

小结

• D&C将问题逐步分解。使用D&C处理列表时，基线条件很可能是空数组或只包含一个元
  素的数组。
• 实现快速排序时，请随机地选择用作基准值的元素。快速排序的平均运行时间为O(n log n)。
• 大O表示法中的常量有时候事关重大，这就是快速排序比合并排序快的原因所在。
• 比较简单查找和二分查找时，常量几乎无关紧要，因为列表很长时，O(log n)的速度比O(n) 快得多。
• 快速排序是最快的排序算法之一，也是D&C典范。