神经元模型

MP神经元，多个加权后减去阈值，最后通过激活函数
激活函数最好的就是阶跃函数，但是不连续不可导
可以用Sigmoid代替

感知机和多层网络

感知机由两层神经元组成，输入层接受外界输入信号传递给输出层，输出层是MP
神经元（阈值逻辑单元）感知机能够容易地实现逻辑与、或、非运算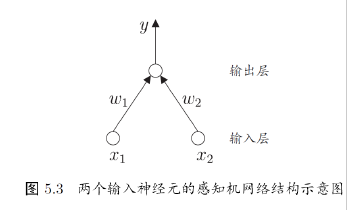

若两类模式线性可分, 则感知机的学习过程一定会收敛；否则感知机的学习过程将会发生震荡
单层感知机的学习能力非常有限, 只能解决线性可分问题。事实上, 与、或、非问题是线性可分的, 因此感知机学习过程能够求得适当的权值向量，而异或问题不是线性可分的, 感知机学习不能求得合适解。可以用多层感知机

输出层与输入层之间的一层神经元, 被称之为隐层或隐含层, 隐含层和输出层神经元都是具有激活函数的功能神经元

多层前馈神经网络
每层神经元与下一层神经元全互联, 神经元之间不存在同层连接也不存在跨层连接

误差逆传播算法

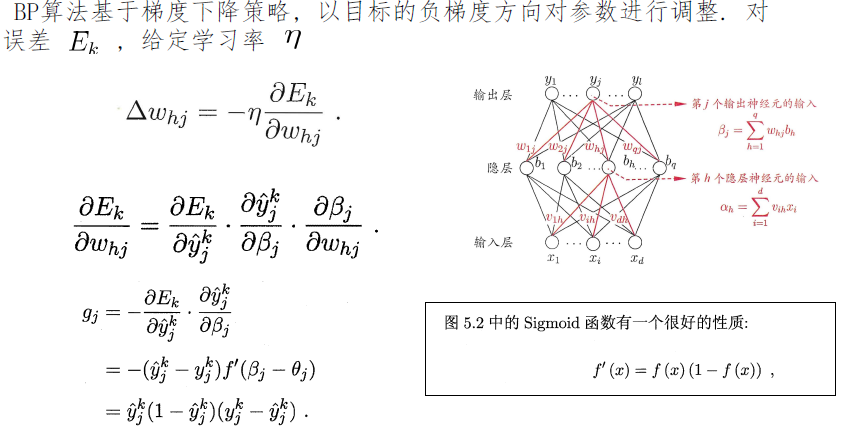
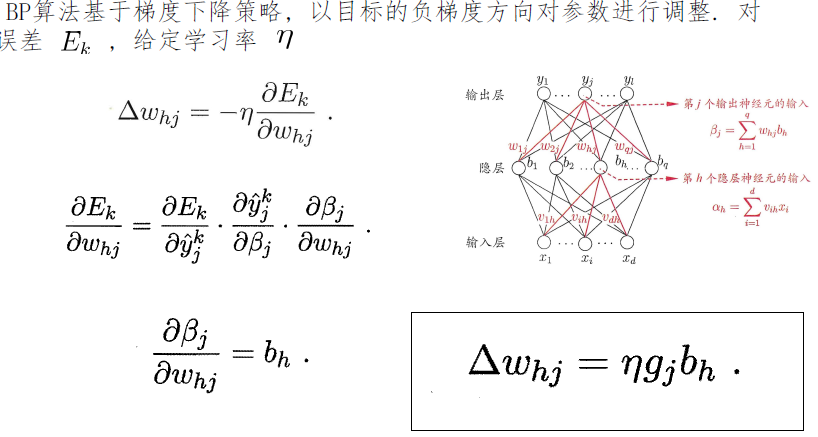
1. 标准 BP 算法
   1. 每次针对单个训练样例更新权值与阈值.
   2. 参数更新频繁, 不同样例可能抵消, 需要多次迭代.
2. 累计 BP 算法
   1. 其优化的目标是最小化整个训练集上的累计误差
   2. 读取整个训练集一遍才对参数进行更新, 参数更新频率较低.

但在很多任务中, 累计误差下降到一定程度后, 进一步下降会非常缓慢,这时标准BP算法往往会获得较好的解, 尤其当训练集非常大时效果更明显.

多层前馈网络表示能力
只需要一个包含足够多神经元的隐层, 多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数

多层前馈网络局限

1. 神经网络由于强大的表示能力, 经常遭遇过拟合。表现为：训练误差持续降低, 但测试误差却可能上升
2. 如何设置隐层神经元的个数仍然是个未决问题. 实际应用中通常使用“试错法”调整

缓解过拟合的策略

1. 早停：在训练过程中, 若训练误差降低, 但验证误差升高, 则停止训练
2. 正则化：在误差目标函数中增加一项描述网络复杂程度的部分, 例如连接权值与阈值的平方和

全局最小与局部极小

梯度为零，且误差函数小于周边即局部最小
可能有多个局部最小，但是只有一个全局最小

1. 模拟退火技术 [Aarts and Korst, 1989]. 每一步都以一定的概率接受比当前解更差的结果, 从而有助于跳出局部极小.
2. 随机梯度下降. 与标准梯度下降法精确计算梯度不同, 随机梯度下降法在计算梯度时加入了随机因素.
3. 遗传算法 [Goldberg, 1989]. 遗传算法也常用来训练神经网络以更好地逼近全局极小.

其他常见神经网络

RBF神经网络

ART网络

SOM网络

级联相关网络

Elman网络

Boltzmann 机

深度学习

1. 增加隐层神经元的数目 (模型宽度)
2. 加隐层数目（模型深度）
3. 从增加模型复杂度的角度看, 增加隐层的数目比增加隐层神经元的数目更有效. 这是因为增加隐层数不仅增加额拥有激活函数的神经元数目,还增加了激活函数嵌套的层数
4. 多隐层网络难以直接用经典算法（例如标准BP算法）进行训练, 因为误差在多隐层内逆传播时, 往往会”发散”而不能收敛到稳定状态.

复杂模型训练方法

预训练+微调的方法

1. 预训练就是逐层进行训练
2. 微调就是预训练结束之后，在整个网络进行微调

联合局部最优找全局最优

权共享

一组神经元使用相同的连接权值.
权共享策略在卷积神经网络(CNN)[LeCun and Bengio, 1995; LeCun et al. , 1998]中发挥了重要作用.

卷积神经网络

1. 卷积层
2. 池化层
3. 连接层

一般用max(0,x)替换Sigmoid