线性模型的优点

• 形式简单、易于建模
• 可解释性
• 非线性模型的基础
• 引入层级结构或高维映射

回归任务

目的：学得一个线性模型以尽可能准确地预测实值输出标记

对于属性的处理，注意区分

1. 有“序”关系：连续化为连续值
2. 无“序”关系：有k个属性值，则转换为k维向量

参数估计：最小二乘法
最小化均方误差，分别对w和b求导可以得到闭式解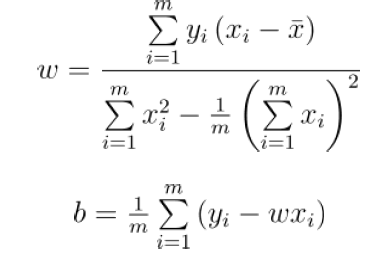

多元线性回归
齐次表达，在X的最后加上一列1，然后就可以把w和b拼接
还是使用最小二乘法进行估计

还有可能是在线性函数的外面套上一层函数，比如说对数线性回归
这个函数的反函数成为联系函数，单调可微函数

二分类任务

对数几率回归

把线性回归的结果和分类标记联系
单位阶跃函数，很可惜不连续

代替函数：对数几率函数，Sigmoid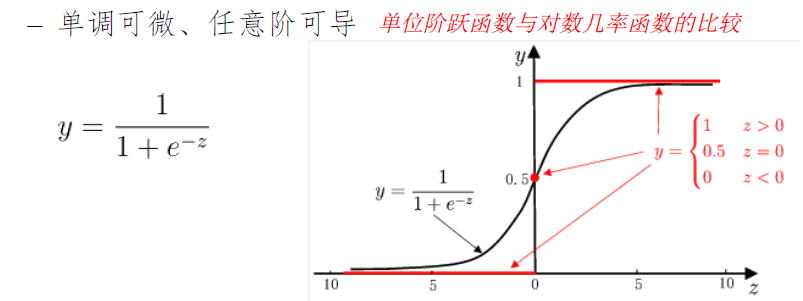

对数几率回归的优势

1. 无需事先假设数据分布
2. 可得到“类别”的近似概率预测
3. 可直接应用现有数值优化算法求取最优解

y理解为样本是正例的概率，进而有

也就是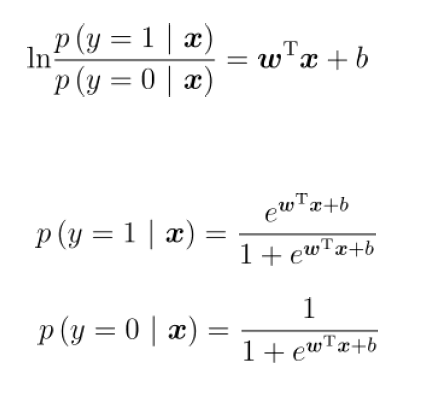

怎么估计参数：极大似然方法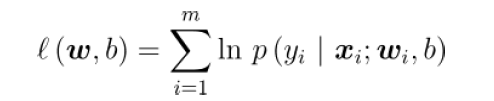

主要的思路

1. 引入了Sigmoid函数，把线性回归和离散的标签之间建立了联系
2. Sigmoid光滑，高阶可导
3. 可以直接得到类别的概率估计

4. 转化为一个极大似然函数的求解

   优势

5. 有类别概率估计输出

6. 可以拓展到多类
7. 逻辑回归有唯一最优解（凸函数）

线性判别分析

让同类尽可能的近，不同类尽可能的远，可用做聚类降维

1. 欲使同类样例的投影点尽可能接近，可以让同类样例投影点的协方差尽可能小
2. 欲使异类样例的投影点尽可能远离，可以让类中心之间的距离尽可能大

分子是类间距离
分母是类内距离
分子分母分别化简得到类内散度矩阵和类间散度矩阵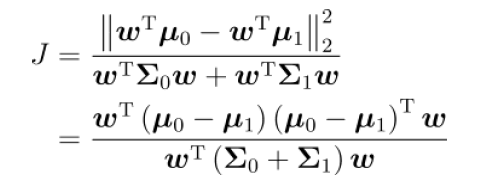

主要建模思想：

1. 寻找线性超平面，使得同类样例的投影点尽可能接近，异类样例的投影点尽可能远离
2. 得到广义瑞利商形式，设计巧妙

3. 得到最优解，是个闭式解

   历史地位

4. LDA能够用于分类任务，但是因为其目标函数不直接对应经验风险，性能不如直接优化经验风险的方法

5. 因LDA投影点有效地得到类别区分方向，保留大量类别之前的判别信息，LDA成为数据降维最主流的方法之一

多分类任务

多分类学习方法

1. 利用二分类分类器解决问题
2. 对问题拆分，多个二分类分类器
3. 最后集成得到结果

一对一 OvO

N个类别两两配对，即N(N-1)/2 个二类任务
每一个任务都有一个分类器
新样本提交给所有分类器预测N(N-1)/2 个分类结果
投票产生最终分类结果，被预测最多的类别为最终类别

一对其余 OvR

某一类是正例，其他的都是反例，N个分类任务
预测的时候就有N个结果，比较一下分类器的置信度

多对多 MvM

把几类作为正类，把几类作为负类

纠错输出码ECOC
以下图为例子
设置5次划分，从纵向来看可以得到下表

然后理论上
f1对测试样本输出1，则说明样本理论上是2，同理其他的分类器
因此从横向看可以得到理论上某一类的样本得到各个分类器的回答
进而可以让测试样例得到的输出去匹配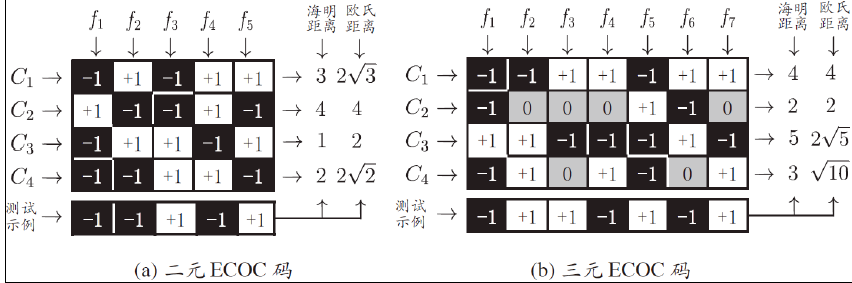

学习策略对比

一对一

1. 存储和测试的开销时间大
   1. 有n^2级别的分类器
   2. 测试的时候需要把测试数据放入n^2的分类器
2. 但是训练时间短，因为对于每一个分类器而言，只需要训练自己所在的两个类别的数据，如果不是A也不是B的样本就不用训练了

一对其余

1. 存储和测试的时间短，因为只有N个分类器
2. 训练的时候每一个分类器需要用到所有的样本，每一个分类都可以构造出是自己类和不是自己类的数据

预测性能和数据的分布有关系
**

类别不平衡问题

欠采样：直接删除一部分的负例
过采样：增加一部分的正例
阈值移动