概述

决策树的建立就是对数据进行划分
递归终止条件

1. 所有的数据都是同一个类别的
2. 当前属性集为空，或所有样本在所有属性上取值相同
3. 当前结点包含的样本集合为空

划分选择

怎么选择最优的划分属性
希望划分之后尽可能的都是一个类别的，进而起到分类的作用
即希望划分之后纯度上升

1. 信息增益
2. 增益率
3. 基尼系数

信息熵

信息增益

问题：
信息增益指标偏好于取值数目较多的属性
比如把编号作为一个划分属性，因为划分的更细，每一个类的内部更纯

增益率

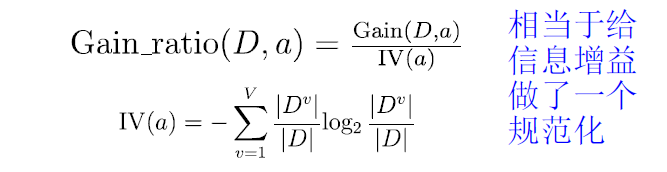
如果说属性a的可以取的值越多，则IV就会越大
问题：增益率准则 偏好 取值数较少的属性
C4.5实现：先找出 信息增益 ⾼于平均⽔平的属性。从中选 增益率 最⾼的属性

基尼系数

用基尼系数度量数据内部的混乱程度
随机选择两个样本，他们不同的概率即基尼系数
基尼系数越低越纯

剪枝处理

决策树容易过拟合，决策树决策分⽀过多
以致于把训练集⾃⾝的⼀些特点当做所有数据都具有的⼀般性质⽽导致的过拟合

预剪枝

在决策树生成的时候就要判断当前的划分能不能带来提升，如果不能就不划分了
停止划分并标记当前最多的样本类别作为这个节点的类别
优点

1. 降低过拟合⻛险
2. 显著减少训练时间和测试时间开销

缺点

1. ⽋拟合⻛险：有些分⽀的当前划分虽然不能提升泛化性能，但在其基础上进⾏的后续划分却有可能导致性能显著提⾼。
2. 预剪枝基于“贪⼼”本质禁⽌这些分⽀展开，带来了⽋拟合⻛险

后剪枝

建立好整个树之后
从底层开始扫描，尝试合并节点
优点

1. 后剪枝⽐预剪枝保留了更多的分⽀，⽋拟合⻛险⼩泛化性能往往优于预剪枝决策树

缺点

1. 训练时间开销⼤：后剪枝过程是在⽣成完全决策树之后进⾏的，需要⾃底向上对所有⾮叶结点逐⼀考察；其训练时间要远⼤于预剪枝决策树

数据处理

连续值处理

使用二分法，把两个数值之间的中点作为划分点
连续值的属性在后面的子节点还能用

缺失值处理

缺失值的属性怎么评价优劣？
在数据集A属性上没有缺失的子集上评价
最外层是无缺失占总体，内部是某取值的样本占的比例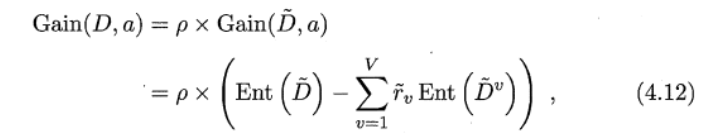

带有缺失值的属性怎么划分？
没有缺失的样本直接弄就行
带有缺失的样本算进所有的子节点，但是乘上了取值样本的占比加入

多变量决策树

单变量的决策树的非叶节点是一个单变量的不等式判断
多变量的决策树可以是多个变量的不等式，举个例子就是一个多元线性回归的式子，使用了多个变量