基本贝叶斯定理
两个问题

  1. 怎么表示文档
  2. 怎么在文档表示和类别概率之间交互

文本表示例子：词袋模型

直接统计一个文档里面所有词的出现的次数

  1. Bernoulli document model：使用一个二元的数组，表示一个词的出现与否
  2. Multinomial document model：使用一个整数数组，表示出现的频率

Bernoulli document model

计算某个类别内，含有词语x的文档数量，除这个类别的文档数目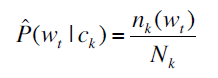
image.png
某个类别文档数目除于总的：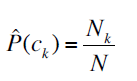
image.png

第一个和第二个公式是在描述一个观察到类别，看到文档的概率，乘上类别概率就是全概率
中间的所有变量从上面可以获取。D_it是一个词是否在这个文档里的标识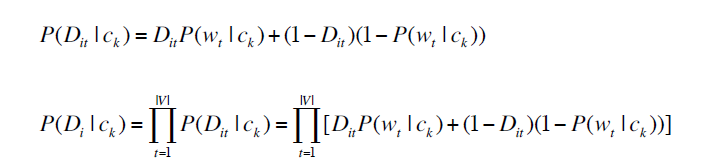
image.png

Multinomial document model

ni是i文档总得词数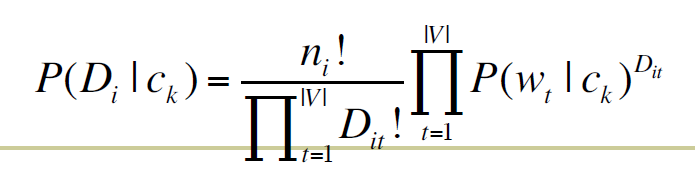
image.png
模型所需要的参数和上一个模型是一样的

分子是某个类别里的文档含有这个词的数量
分母是同样的，只不过是对所有的词都进行统计和累加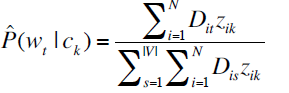
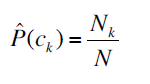
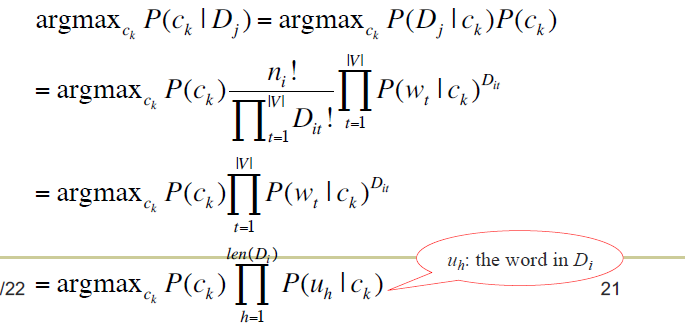
image.png
image.png
image.png

仍然还是会出现零概率的问题，就需要进行平滑操作：加一平滑策略

重构问题

特征向量

认为原文输入一个特征向量
image.png
image.png
然后每一个类别都有一个线性函数，根据这个特征计算一个分数，然后选择最大

线性函数

比如说：线性函数可以是贝叶斯
和前面差不多，把这种概率作为分数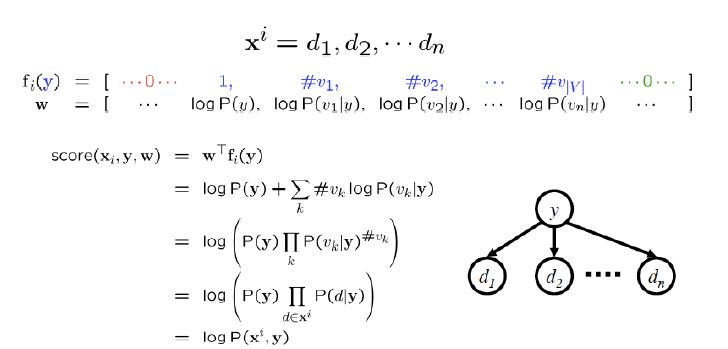
image.png

怎么学习权重
用一个损失函数来衡量错误的代价，然后最小化错误代价

最大化熵
image.png
image.png

文本表示问题

特征选择

  1. 高维空间
  2. 消除噪音特征和低消特征
  3. 选择一个子集构造鲁棒的模型

特征清洗利用

  1. 停用词
  2. 词频
  3. 互信息（选择高互信息）
  4. 卡方

互信息

image.png
image.png

卡方

可以检测两个东西的无关性
image.png
高的卡方结果说明独立假设不成立
如果说二者不相关，那就说明这个东西对推断分类有用，也就是好特征

一个是预期，预期如果不相关就应该 P（AB）=P（A）P(B)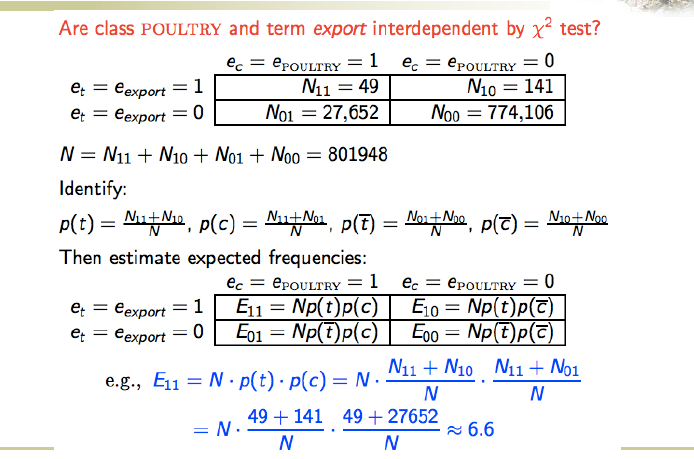
image.png

TF-IDF

tf是重要词的频率，具体的计算就是频率除于最高频
idf希望过滤掉在很多文档里都高频的词，df即包含词语i的文档个数，idf是log2（N/df）
最后的权重就是tf*idf

评估策略

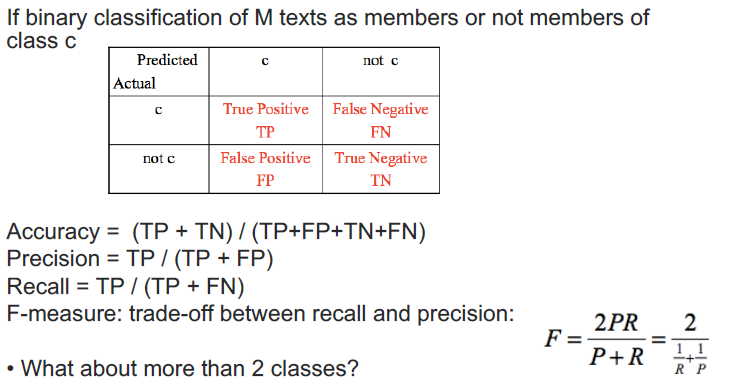
image.png
Acc准确率就是正确率的除于总的
Precision是把Positive挑出来的能力，即模型认为的positive里多少是真的
Recall是所有的正确你挑出来多少，主要侧重点涵盖的完全

多类别的计算

  1. macro：分别计算后平均
  2. micro：混淆矩阵，即合并