原文地址

前言

前段时间在掘金看到一个热帖 今天又懒得加班了，能写出这两个算法吗？带你去电商公司写商品中心，里面提到了一个比较有意思故事，大意就是一个看似比较简单的电商 sku 的全排列组合算法，但是却有好多人没能顺利写出来。有一个毕业生小伙子在面试的时候给出了思路，但是进去以后还是没写出来，羞愧跑路~
其实排列组合是一个很经典的算法，也是对递归回溯法的一个实践运用，本篇文章就以带你学习一个标准「排列组合求解模板」，耐心看完，你会有更多收获。

需求

需求描述起来很简单，有这样三个数组：

  1. let names = ["iPhone X", "iPhone XS"]
  3. let colors = ["黑色", "白色"]
  5. let storages = ["64g", "256g"]

需要把他们的所有组合穷举出来，最终得到这样一个数组：

  1. [
  2.   ["iPhone X", "黑色", "64g"],
  3.   ["iPhone X", "黑色", "256g"],
  4.   ["iPhone X", "白色", "64g"],
  5.   ["iPhone X", "白色", "256g"],
  6.   ["iPhone XS", "黑色", "64g"],
  7.   ["iPhone XS", "黑色", "256g"],
  8.   ["iPhone XS", "白色", "64g"],
  9.   ["iPhone XS", "白色", "256g"],
  10. ]

由于这些属性数组是不定项的，所以不能简单的用三重的暴力循环来求解了。

思路

如果我们选用递归回溯法来解决这个问题，那么最重要的问题就是设计我们的递归函数。

思路分解

以上文所举的例子来说，比如我们目前的属性数组就是：names、colors、storages，首先我们会处理 names 数组，很显然对于每个属性数组，都需要去遍历它，然后一个一个选择后再去和 下一个数组的每一项进行组合。
我们设计的递归函数接受两个参数：

  • index 对应当前正在处理的下标，是 names 还是 colors 或是 storage。
  • prev 上一次递归已经拼接成的结果，比如 [‘iPhone X’, ‘黑色’]。

进入递归函数：

  1. 处理属性数组的下标0：假设我们在第一次循环中选择了 iPhone XS，那此时我们有一个未完成的结果状态，假设我们叫它 prev，此时 prev = [‘iPhone XS’]。
  2. 处理属性数组的下标1：那么就处理到 colors 数组的了，并且我们拥有 prev，在遍历 colors 的时候继续递归的去把 prev 拼接成 prev.concat(color)，也就是 [‘iPhone XS’, ‘黑色’] 这样继续把这个 prev 交给下一次递归。
  3. 处理属性数组的下标2：那么就处理到 storages 数组的了，并且我们拥有了 name + color 的 prev，在遍历 storages 的时候继续递归的去把 prev 拼接成 prev.concat(storage)，也就是 [‘iPhone XS’, ‘黑色’, ‘64g’]，并且此时我们发现处理的属性数组下标已经到达了末尾，那么就放入全局的结果变量 res 中，作为一个结果。

    编码实现

  1. let names = ["iPhone X", "iPhone XS"]
  3. let colors = ["黑色", "白色"]
  5. let storages = ["64g", "256g"]
  7. let combine = function (...chunks) {
  8.   let res = []
  10.   let helper = function (chunkIndex, prev) {
  11.     let chunk = chunks[chunkIndex]
  12.     let isLast = chunkIndex === chunks.length - 1
  13.     for (let val of chunk) {
  14.       let cur = prev.concat(val)
  15.       if (isLast) {
  16.         // 如果已经处理到数组的最后一项了 则把拼接的结果放入返回值中
  17.         res.push(cur)
  18.       } else {
  19.         helper(chunkIndex + 1, cur)
  20.       }
  21.     }
  22.   }
  24.   // 从属性数组下标为 0 开始处理
  25.   // 并且此时的 prev 是个空数组
  26.   helper(0, [])
  28.   return res
  29. }
  31. console.log(combine(names, colors, storages))

递归树图

画出以 iPhone X 这一项为起点的递归树图，当然这个问题是一个多个根节点的树，请自行脑补 iPhone XS 为起点的树，子结构是一模一样的。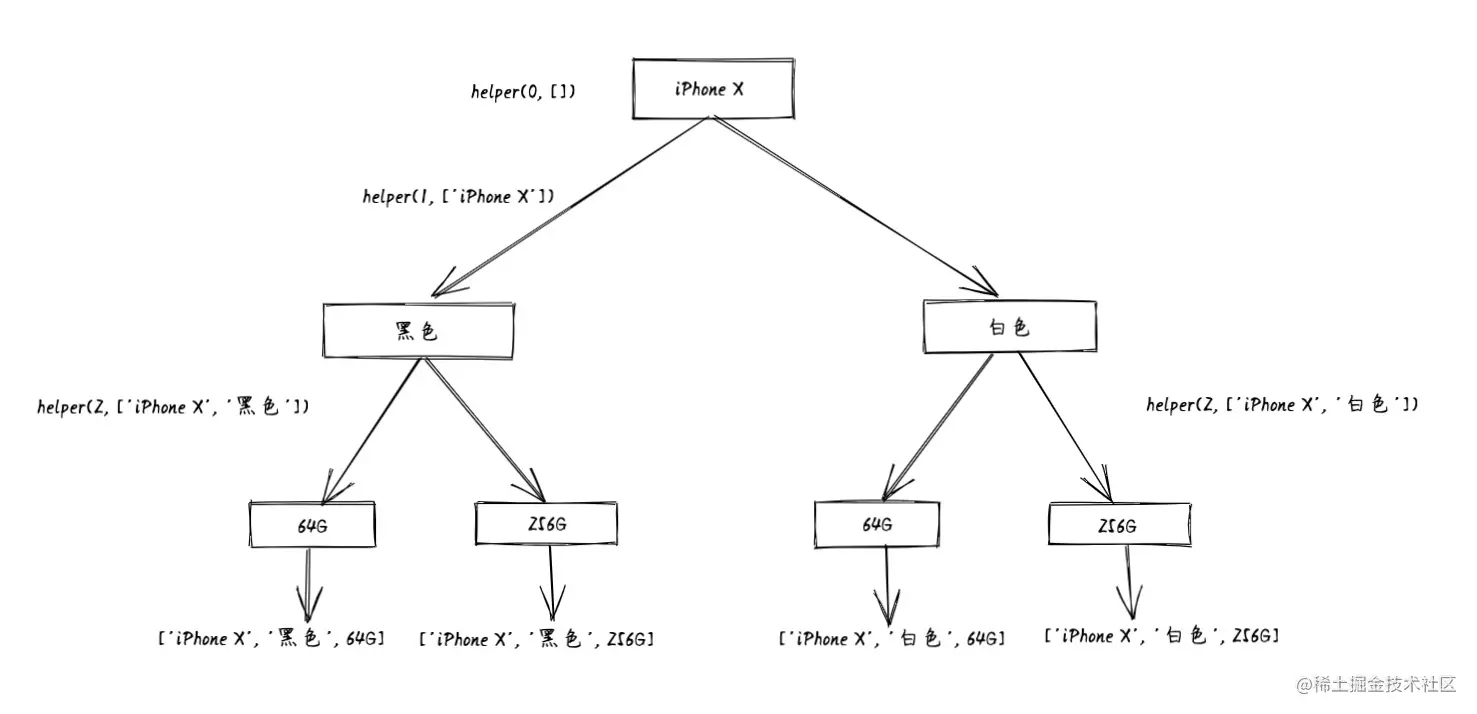
2021/03/01 【 前端电商 sku 的全排列算法很难吗？学会这个套路，彻底掌握排列组合。】 - 图1

万能模板

为什么说这种接法是排列组合的「万能模板呢」？来看一下 LeetCode 上的真题。

组合-77

77. 组合 这是一道难度为 medium 的问题，其实算是比较有难度的问题了：

问题

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。
示例:

  1. 输入: n = 4, k = 2
  2. 输出:
  3. [
  4.   [2,4],
  5.   [3,4],
  6.   [2,3],
  7.   [1,2],
  8.   [1,3],
  9.   [1,4],
  10. ]
  1. let combine = function (n, k) {
  2.   let ret = []
  4.   let helper = (start, prev) => {
  5.     let len = prev.length
  6.     if (len === k) {
  7.       ret.push(prev)
  8.       return
  9.     }
  11.     for (let i = start; i <= n; i++) {
  12.       helper(i + 1, prev.concat(i))
  13.     }
  14.   }
  15.   helper(1, [])
  16.   return ret
  17. }

可以看出这题和我们求解电商排列组合的代码竟然如此相似。只需要设计一个接受 start排列起始位置、prev上一次拼接结果为参数的递归 helper函数，
然后对于每一个起点下标 start，先拼接上 start位置对应的值，再不断的再以其他剩余的下标作为起点去做下一次拼接。当 prev 这个中间状态的拼接数组到达题目的要求长度 k后，就放入结果数组中。

优化

在这个解法中，有一些递归分支是明显不可能获取到结果的，我们每次递归都会循环尝试 <= n的所有项去作为start，假设我们要求的数组长度 k = 3，最大值 n = 4。
而我们以 prev = [1]，再去以 n = 4 为 start 作为递归的起点，那么显然是不可能得到结果的，因为 n = 4 的话就只剩下 4这一项可以拼接了，最多也就拼接成 [1, 4]，不可能满足 k = 3 的条件。
所以在进入递归之前，就果断的把这些“废枝”给减掉。这就叫做「剪枝」

  1. let combine = function (n, k) {
  2.   let ret = []
  4.   let helper = (start, prev) => {
  5.     let len = prev.length
  6.     if (len === k) {
  7.       ret.push(prev)
  8.       return
  9.     }
  11.     // 还有 rest 个位置待填补
  12.     let rest = k - prev.length
  13.     for (let i = start; i <= n; i++) {
  14.       if (n - i + 1 < rest) {
  15.         continue
  16.       }
  17.       helper(i + 1, prev.concat(i))
  18.     }
  19.   }
  20.   helper(1, [])
  21.   return ret
  22. }

相似题型

当然，力扣中可以套用这个模板的相似题型还有很多，而且大多数难度都是 medium的，比如快手的面试题子集 II-90，可以看出排列组合的递归解法还是有一定的难度的。

总结

排列组合问题并不是空中楼阁，在实际工作中也会经常遇到这种场景，掌握了递归回溯的标准模板当然不是为了让你死记硬背套公式，而是真正的理解它。遇到需要递归解决的问题。

  1. 画出递归树状图，找出递归公式。
  2. 对于不可能达成条件的分支递归，进行合理的「剪枝」。

希望阅读完本篇文章的你，能对递归和排列组合问题有进一步的理解和收获。