我们现在要开始做题啦！
万里长征第一步，仍然是数组。
单纯针对数组来考察的题目，总体来说，都不算太难——数组题目要想往难了出，基本都要结合排序、二分和动态规划这些相对复杂的算法思想才行。
咱们本节要解决的正是这一类“不算太难”的数组题目——并不是只有难题才拥有成为真题的入场券，一道好题不一定会难，它只要能够反映问题就可以了。
本节所涉及的题目在面试中普遍具有较高的出镜率、同时兼具一定的综合性，对培养大家的通用解题能力大有裨益 。
相信这节你会学得很开心，在轻松中收获自己的第一份算法解题锦囊。

Map 的妙用——两数求和问题

真题描述： 给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。

示例:

给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9 所以返回 [0, 1]

思路分析：

一个“淳朴”的解法

这道题相信很多同学看一眼就很快能得出一个最基本的思路：两层循环来遍历同一个数组；第一层循环遍历的值记为 a，第二层循环时遍历的值记为 b；若 a+b = 目标值，那么 a 和 b 对应的数组下标就是我们想要的答案。

对“淳朴”解法的反思

大家以后做算法题的时候，要有这样的一种本能：当发现自己的代码里有两层循环时，先反思一下，能不能用空间换时间，把它优化成一层循环。
因为两层循环很多情况下都意味着 O(n^2) 的复杂度，这个复杂度非常容易导致你的算法超时。即便没有超时，在明明有一层遍历解法的情况下，你写了两层遍历，面试官对你的印象分会大打折扣。

空间换时间，Map 来帮忙

拿我们这道题来说，其实二层遍历是完全不必要的。
大家记住一个结论：几乎所有的求和问题，都可以转化为求差问题。 这道题就是一个典型的例子，通过把求和问题转化为求差问题，事情会变得更加简单。
我们可以在遍历数组的过程中，增加一个 Map 来记录已经遍历过的数字及其对应的索引值。然后每遍历到一个新数字的时候，都回到 Map 里去查询 targetNum 与该数的差值是否已经在前面的数字中出现过了。若出现过，那么答案已然显现，我们就不必再往下走了。
我们以 nums = [2, 7, 11, 15] 这个数组为例，来模拟一下这个思路：
第一次遍历到 2，此时 Map 为空：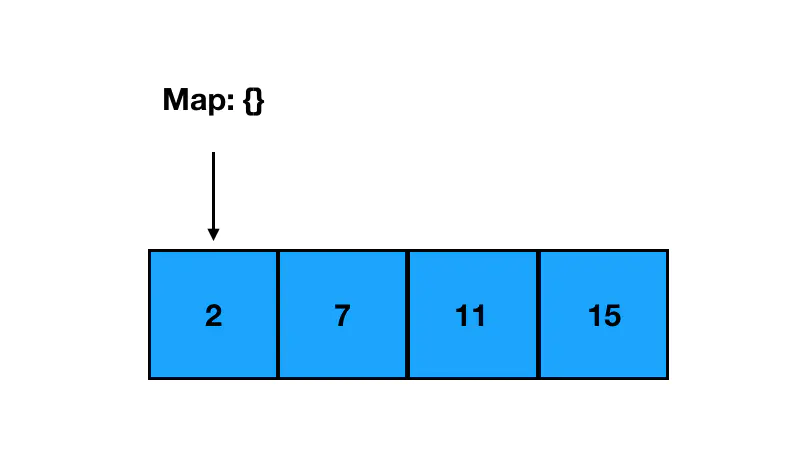
7 | 数组的应用——真题归纳与解读 - 图1
以 2 为 key，索引 0 为 value 作存储，继续往下走；遇到了 7：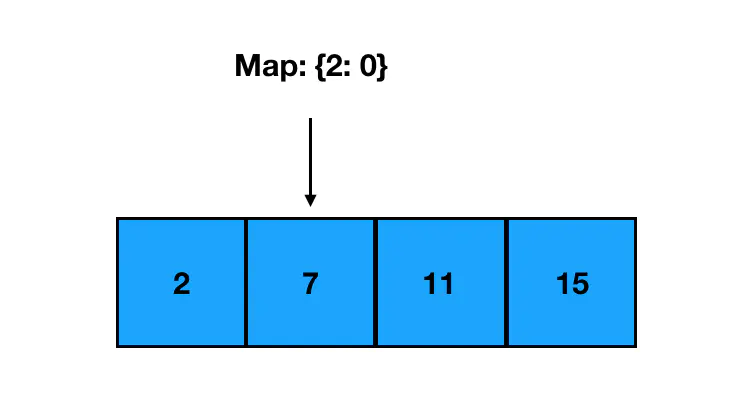
7 | 数组的应用——真题归纳与解读 - 图2
计算 targetNum 和 7 的差值为2，去 Map 中检索 2 这个 key，发现是之前出现过的值：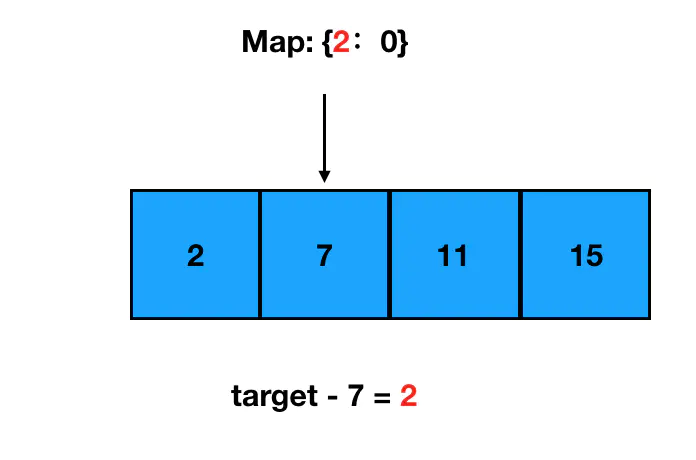
7 | 数组的应用——真题归纳与解读 - 图3 那么 2 和 7 的索引组合就是这道题的答案啦。
键值对存储我们可以用 ES6 里的 Map 来做，如果图省事，直接用对象字面量来定义也没什么问题。

编码实现

  1. /**
  2.  * @param {number[]} nums
  3.  * @param {number} target
  4.  * @return {number[]}
  5.  */
  6. const twoSum = function(nums, target) {
  7.     // 这里我用对象来模拟 map 的能力
  8.     const diffs = {}
  9.     // 缓存数组长度
  10.     const len = nums.length
  11.     // 遍历数组
  12.     for(let i=0;i<len;i++) {
  13.         // 判断当前值对应的 target 差值是否存在（是否已遍历过）
  14.         if(diffs[target-nums[i]]!==undefined) {
  15.             // 若有对应差值，那么答案get！
  16.             return [diffs[target - nums[i]], i]
  17.         }
  18.         // 若没有对应差值，则记录当前值
  19.         diffs[nums[i]]=i
  20.     }
  21. };

tips：这道题也可以用 ES6 中的 Map 来做，你试试呢？

强大的双指针法

合并两个有序数组

真题描述：给你两个有序整数数组 nums1 和 nums2，请你将 nums2 合并到 nums1 中，使 nums1 成为一个有序数组。

说明: 初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。 你可以假设 nums1 有足够的空间（空间大小大于或等于 m + n）来保存 nums2 中的元素。

示例:

输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
输出: [1,2,2,3,5,6]

思路分析

标准解法

这道题没有太多的弯弯绕绕，标准解法就是双指针法。首先我们定义两个指针，各指向两个数组生效部分的尾部：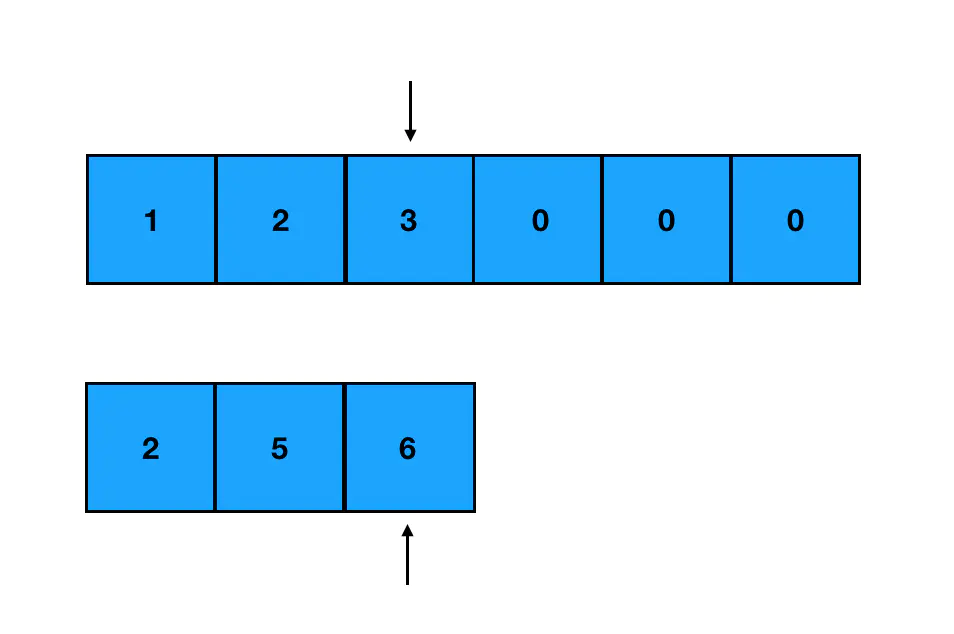
7 | 数组的应用——真题归纳与解读 - 图4
每次只对指针所指的元素进行比较。取其中较大的元素，把它从 nums1 的末尾往前面填补：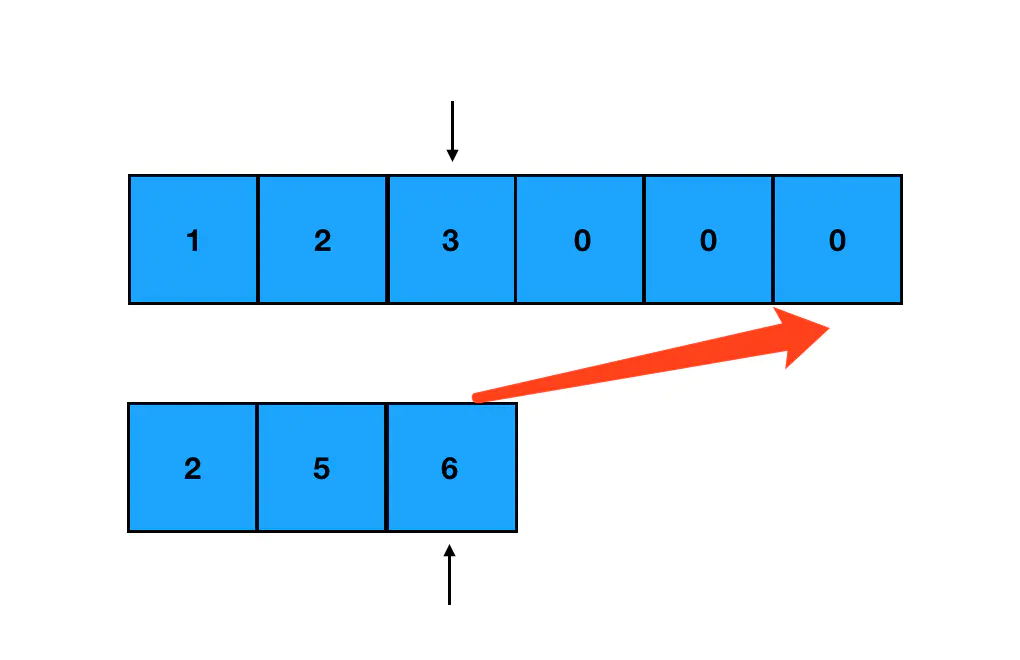
7 | 数组的应用——真题归纳与解读 - 图5 这里有一点需要解释一下：
为什么是从后往前填补？因为是要把所有的值合并到 nums1 里，所以说我们这里可以把 nums1 看做是一个“容器”。但是这个容器，它不是空的，而是前面几个坑有内容的。如果我们从前往后填补，就没法直接往对应的坑位赋值了（会产生值覆盖）。
从后往前填补，我们填的都是没有内容的坑，这样会省掉很多麻烦。
由于 nums1 的有效部分和 nums2 并不一定是一样长的。我们还需要考虑其中一个提前到头的这种情况：

  1. 如果提前遍历完的是 nums1 的有效部分，剩下的是 nums2。那么这时意味着 nums1 的头部空出来了，直接把 nums2 整个补到 nums1 前面去即可。

  2. 如果提前遍历完的是 nums2，剩下的是 nums1。由于容器本身就是 nums1，所以此时不必做任何额外的操作。

    编码实现：

    1. /**
    2. * @param {number[]} nums1
    3. * @param {number} m
    4. * @param {number[]} nums2
    5. * @param {number} n
    6. * @return {void} Do not return anything, modify nums1 in-place instead.
    7. */
    8. const merge = function(nums1, m, nums2, n) {
    9.  // 初始化两个指针的指向，初始化 nums1 尾部索引k
    10.  let i = m - 1, j = n - 1, k = m + n - 1
    11.  // 当两个数组都没遍历完时，指针同步移动
    12.  while(i >= 0 && j >= 0) {
    13.      // 取较大的值，从末尾往前填补
    14.      if(nums1[i] >= nums2[j]) {
    15.          nums1[k] = nums1[i] 
    16.          i-- 
    17.          k--
    18.      } else {
    19.          nums1[k] = nums2[j] 
    20.          j-- 
    21.          k--
    22.      }
    23.  }
    25.  // nums2 留下的情况，特殊处理一下 
    26.  while(j>=0) {
    27.      nums1[k] = nums2[j]  
    28.      k-- 
    29.      j--
    30.  }
    31. };

    找点乐子：
    上面我们给出的，是面试官最喜欢看到的一种解法，这种解法适用于各种语言。
    但是就 JS 而言，我们还可以“另辟蹊径”，仔细想想，你有什么妙招？

    三数求和问题

    双指针法能处理的问题多到你想不到。不信来瞅瞅两数求和它儿子——三数求和问题！
    俗话说，青出于蓝而胜于蓝，三数求和虽然和两数求和只差了一个字，但是思路却完全不同。

    真题描述：给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例：

给定数组 nums = [-1, 0, 1, 2, -1, -4]， 满足要求的三元组集合为： [ [-1, 0, 1], [-1, -1, 2] ]

思路分析

三数之和延续两数之和的思路，我们可以把求和问题变成求差问题——固定其中一个数，在剩下的数中寻找是否有两个数和这个固定数相加是等于0的。
虽然乍一看似乎还是需要三层循环才能解决的样子，不过现在我们有了双指针法，定位效率将会被大大提升，从此告别过度循环~
（这里大家相信已经能察觉出来双指针法的使用场景了，一方面，它可以做到空间换时间；另一方面，它也可以帮我们降低问题的复杂度。）
双指针法用在涉及求和、比大小类的数组题目里时，大前提往往是：该数组必须有序。否则双指针根本无法帮助我们缩小定位的范围，压根没有意义。因此这道题的第一步是将数组排序：

  1. nums = nums.sort((a,b)=>{
  2.     return a-b
  3. })

然后，对数组进行遍历，每次遍历到哪个数字，就固定哪个数字。然后把左指针指向该数字后面一个坑里的数字，把右指针指向数组末尾，让左右指针从起点开始，向中间前进：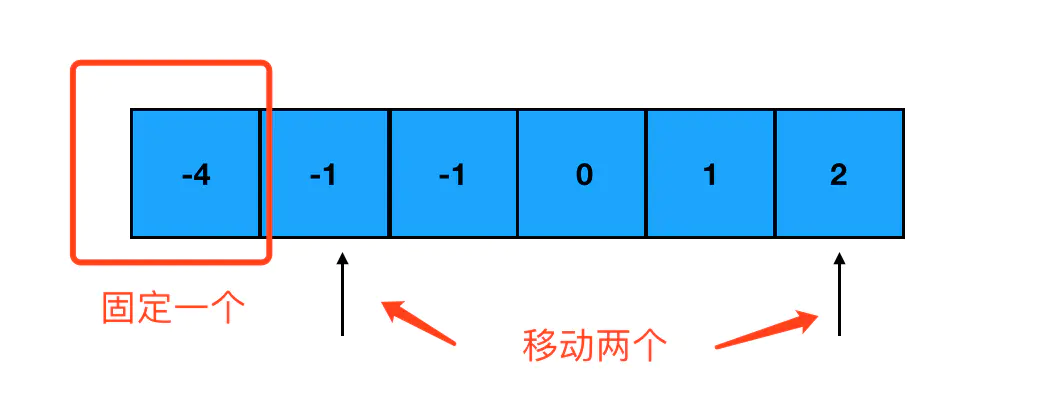
7 | 数组的应用——真题归纳与解读 - 图6 每次指针移动一次位置，就计算一下两个指针指向数字之和加上固定的那个数之后，是否等于0。如果是，那么我们就得到了一个目标组合；否则，分两种情况来看：

  • 相加之和大于0，说明右侧的数偏大了，右指针左移
  • 相加之和小于0，说明左侧的数偏小了，左指针右移

tips：这个数组在题目中要求了“不重复的三元组”，因此我们还需要做一个重复元素的跳过处理。这一点在编码实现环节大家会注意到。

编码实现

  1. /**
  2.  * @param {number[]} nums
  3.  * @return {number[][]}
  4.  */
  5. const threeSum = function(nums) {
  6.     // 用于存放结果数组
  7.     let res = [] 
  8.     // 给 nums 排序
  9.     nums = nums.sort((a,b)=>{
  10.         return a-b
  11.     })
  12.     // 缓存数组长度
  13.     const len = nums.length
  14.     // 注意我们遍历到倒数第三个数就足够了，因为左右指针会遍历后面两个数
  15.     for(let i=0;i<len-2;i++) {
  16.         // 左指针 j
  17.         let j=i+1 
  18.         // 右指针k
  19.         let k=len-1   
  20.         // 如果遇到重复的数字，则跳过
  21.         if(i>0&&nums[i]===nums[i-1]) {
  22.             continue
  23.         }
  24.         while(j<k) {
  25.             // 三数之和小于0，左指针前进
  26.             if(nums[i]+nums[j]+nums[k]<0){
  27.                 j++
  28.                // 处理左指针元素重复的情况
  29.                while(j<k&&nums[j]===nums[j-1]) {
  30.                     j++
  31.                 }
  32.             } else if(nums[i]+nums[j]+nums[k]>0){
  33.                 // 三数之和大于0，右指针后退
  34.                 k--
  36.                // 处理右指针元素重复的情况
  37.                while(j<k&&nums[k]===nums[k+1]) {
  38.                     k--
  39.                 }
  40.             } else {
  41.                 // 得到目标数字组合，推入结果数组
  42.                 res.push([nums[i],nums[j],nums[k]])
  44.                 // 左右指针一起前进
  45.                 j++  
  46.                 k--
  48.                 // 若左指针元素重复，跳过
  49.                 while(j<k&&nums[j]===nums[j-1]) {
  50.                     j++
  51.                 }  
  53.                // 若右指针元素重复，跳过
  54.                while(j<k&&nums[k]===nums[k+1]) {
  55.                     k--
  56.                 }
  57.             }
  58.         }
  59.     }
  61.     // 返回结果数组
  62.     return res
  63. };

双指针法中的“对撞指针”法

在上面这道题中，左右指针一起从两边往中间位置相互迫近，这样的特殊双指针形态，被称为“对撞指针”。
什么时候你需要联想到对撞指针？
这里我给大家两个关键字——“有序”和“数组”。
没错，见到这两个关键字，立刻把双指针法调度进你的大脑内存。普通双指针走不通，立刻想对撞指针！
即便数组题目中并没有直接给出“有序”这个关键条件，我们在发觉普通思路走不下去的时候，也应该及时地尝试手动对其进行排序试试看有没有新的切入点——没有条件，创造条件也要上。
对撞指针可以帮助我们缩小问题的范围，这一点在“三数求和”问题中体现得淋漓尽致：因为数组有序，所以我们可以用两个指针“画地为牢”圈出一个范围，这个范围以外的值不是太大就是太小、直接被排除在我们的判断逻辑之外，这样我们就可以把时间花在真正有意义的计算和对比上。如此一来，不仅节省了计算的时间，更降低了问题本身的复杂度，我们做题的速度也会大大加快。