4 | 快速上手——从0到1掌握算法面试需要的数据结构（三）

本节我们一起来认识一下树与二叉树。

理解树结构

在理解计算机世界的树结构之前，大家不妨回忆一下现实世界中的树有什么特点：一棵树往往只有一个树根，向上生长后，却可以伸展出无数的树枝、树枝上会长出树叶。由树根从泥土中吸收水、无机盐等营养物质，源源不断地输送到树枝与树叶的那一端。一棵树往往呈现这样的基本形态：

数据结构中的树，首先是对现实世界中树的一层简化：

• 把树根抽象为“根结点”，
• 树枝抽象为“边”，
• 树枝的两个端点抽象为“结点”，
• 树叶抽象为“叶子结点”。

抽象后的树结构如下：

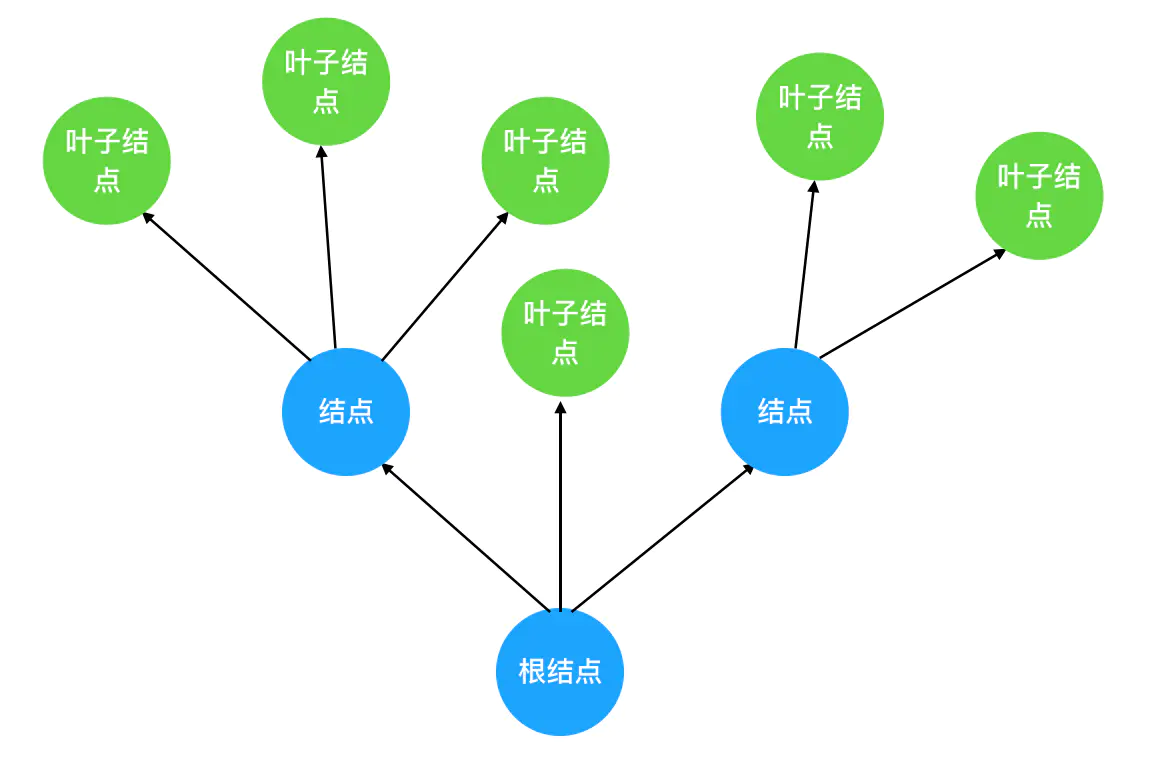
把这棵抽象后的树颠倒一下，就得到了计算机中的树结构：

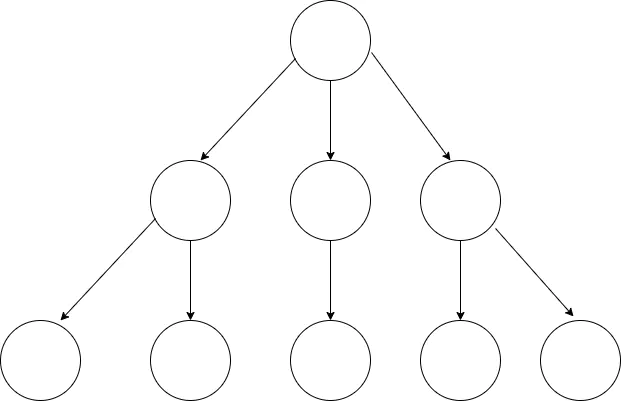
结合这张图，我们来讲解树的关键特性和重点概念。希望大家可以牢记以下几点：

• 树的层次计算规则：根结点所在的那一层记为第一层，其子结点所在的就是第二层，以此类推。
• 结点和树的“高度”计算规则：叶子结点高度记为1，每向上一层高度就加1，逐层向上累加至目标结点时，所得到的的值就是目标结点的高度。树中结点的最大高度，称为“树的高度”。
• “度”的概念：一个结点开叉出去多少个子树，被记为结点的“度”。比如我们上图中，根结点的“度”就是3。
• “叶子结点”：叶子结点就是度为0的结点。在上图中，最后一层的结点的度全部为0，所以这一层的结点都是叶子结点。

  理解二叉树结构

二叉树是指满足以下要求的树：

• 它可以没有根结点，作为一棵空树存在
• 如果它不是空树，那么必须由根结点、左子树和右子树组成，且左右子树都是二叉树。如下图：
  

注意，二叉树不能被简单定义为每个结点的度都是2的树。普通的树并不会区分左子树和右子树，但在二叉树中，左右子树的位置是严格约定、不能交换的。对应到图上来看，也就意味着 B 和 C、D 和 E、F 和 G 是不能互换的。

二叉树的编码实现

在 JS 中，二叉树使用对象来定义。它的结构分为三块：

• 数据域
• 左侧子结点（左子树根结点）的引用
• 右侧子结点（右子树根结点）的引用

在定义二叉树构造函数时，我们需要把左侧子结点和右侧子结点都预置为空：

// 二叉树结点的构造函数
function TreeNode(val) {
    this.val = val;
    this.left = this.right = null;
}

当你需要新建一个二叉树结点时，直接调用构造函数、传入数据域的值就行了：

const node  = new TreeNode(1)

如此便能得到一个值为 1 的二叉树结点，从结构上来说，它长这样：

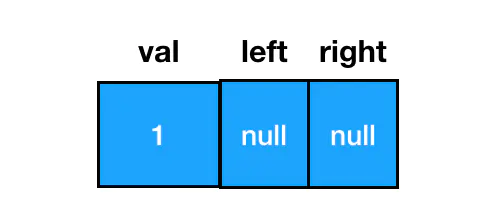
以这个结点为根结点，我们可以通过给 left/right 赋值拓展其子树信息，延展出一棵二叉树。因此从更加细化的角度来看，一棵二叉树的形态实际是这样的：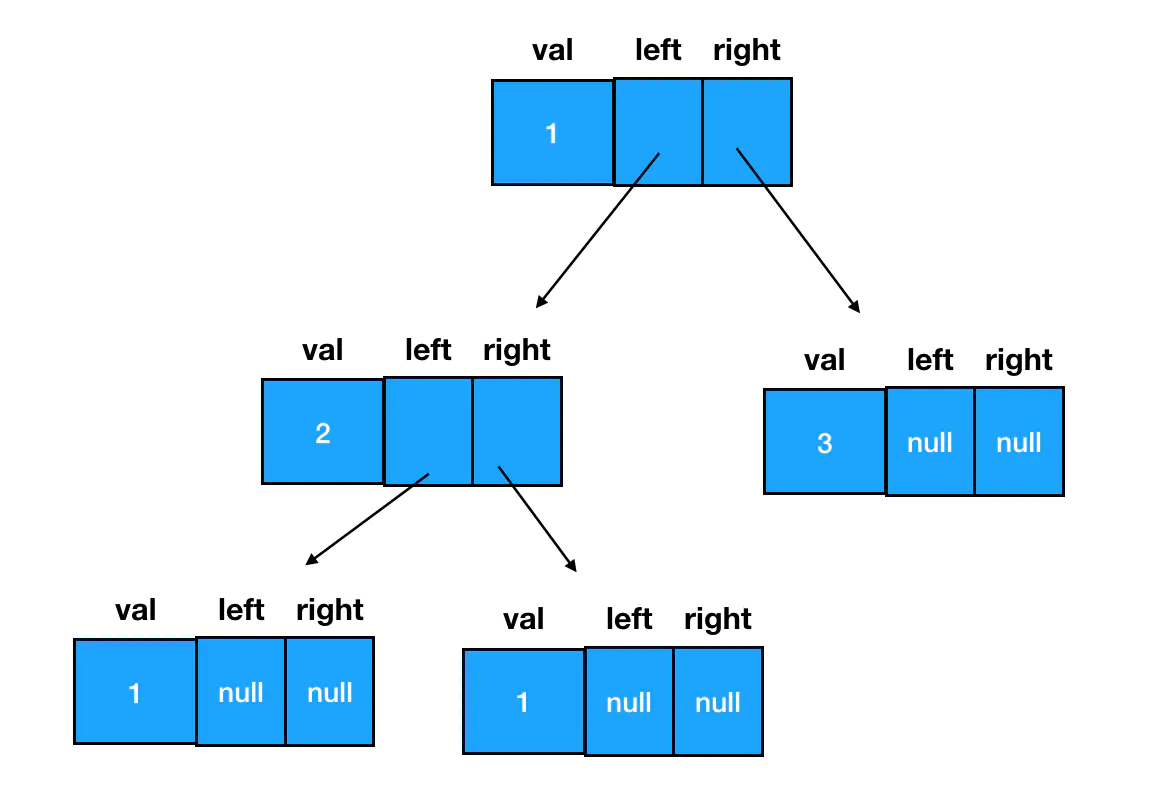

现在各位已经掌握了做二叉树面试题所需要的一系列前置知识。接下来我会带大家一起通过写代码的方式，来搞定二叉树系列里最首当其冲、同时相当热门的考点——二叉树的遍历。