10 | 快慢指针与多指针——玩转链表复杂操作

链表题目中，有一类会涉及到反复的遍历。涉及反复遍历的题目，题目本身虽然不会直接跟你说“你好，我是一道需要反复遍历的题目”，但只要你尝试用常规的思路分析它，你会发现它一定涉及反复遍历；同时，涉及反复遍历的题目，还有一个更明显的特征，就是它们往往会涉及相对复杂的链表操作，比如反转、指定位置的删除等等。
解决这类问题，我们用到的是双指针中的“快慢指针”。快慢指针指的是两个一前一后的指针，两个指针往同一个方向走，只是一个快一个慢。快慢指针严格来说只能有俩，不过实际做题中，可能会出现一前、一中、一后的三个指针，这种超过两个指针的解题方法也叫“多指针法”。
快慢指针+多指针，双管齐下，可以帮助我们解决链表中的大部分复杂操作问题。

快慢指针——删除链表的倒数第 N 个结点

真题描述：给定一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。 示例：

给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个结点后，链表变为 1->2->3->5.

说明：

给定的 n 保证是有效的。

思路分析

小贴士：dummy 结点的使用

上一节我给大家介绍了 dummy 结点：它可以帮我们处理掉头结点为空的边界问题，帮助我们简化解题过程。因此涉及链表操作、尤其是涉及结点删除的题目（对前驱结点的存在性要求比较高），我都建议大家写代码的时候直接把 dummy 给用起来，建立好的编程习惯：

const dummy = new ListNode()
// 这里的 head 是链表原有的第一个结点
dummy.next = head

“倒数”变“正数”

链表的删除我们上节已经讲过，相信都难不倒大家。这道题的难点实际在于这个“倒数第 N 个”如何定位。
考虑到咱们的遍历不可能从后往前走，因此这个“倒数第 N 个” 咱们完全可以转换为“正数第 len - n + 1“个。这里这个 len 代表链表的总长度，比如说咱们链表长为 7，那么倒数第 1 个就是正数第 7 个。按照这个思路往下分析，如果走直接遍历这条路，那么这个 len 就非常关键了。
我们可以直接遍历两趟：第一趟，设置一个变量 count = 0，每遍历到一个不为空的结点，count 就加 1，一直遍历到链表结束为止，得出链表的总长度 len；根据这个总长度，咱们就可以算出倒数第 n 个到底是正数第几个了（M = len - n + 1），那么我们遍历到第M - 1（也就是 len - n） 个结点的时候就可以停下来，执行删除操作（想一想，为什么是第 M-1 个，而不是第 M 个？如果你认真读了我们前面的章节，心中一定会有一个清晰的答案^_^）
不过这种超过一次的遍历必然需要引起我们的注意，我们应该主动去思考，“如果一次遍历来解决这个问题，我可以怎么做？”，这时候，就要请双指针法来帮忙了。

快慢指针登场

按照我们已经预告过的思路，首先两个指针 slow 和 fast，全部指向链表的起始位——dummy 结点：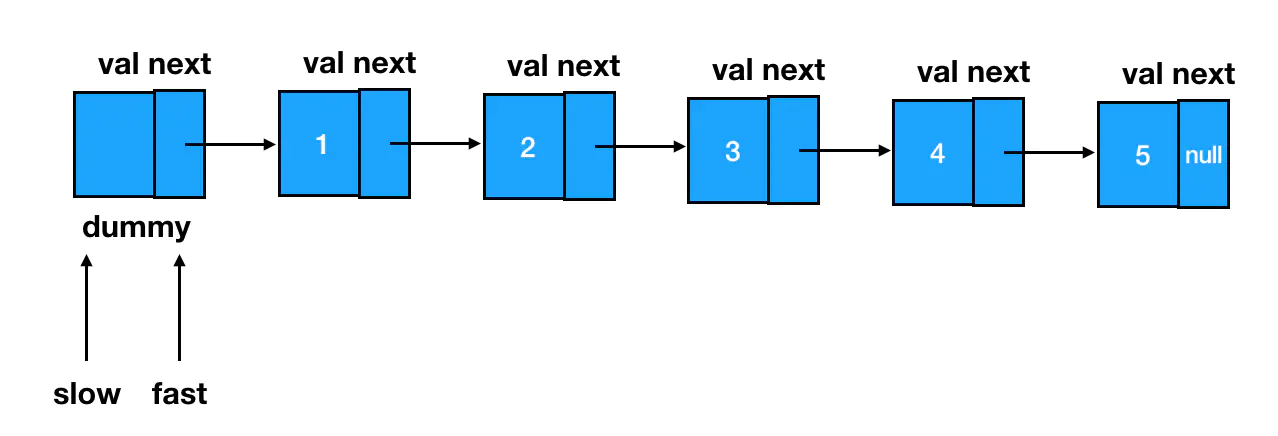

快指针先出发！闷头走上 n 步，在第 n 个结点处打住，这里 n=2：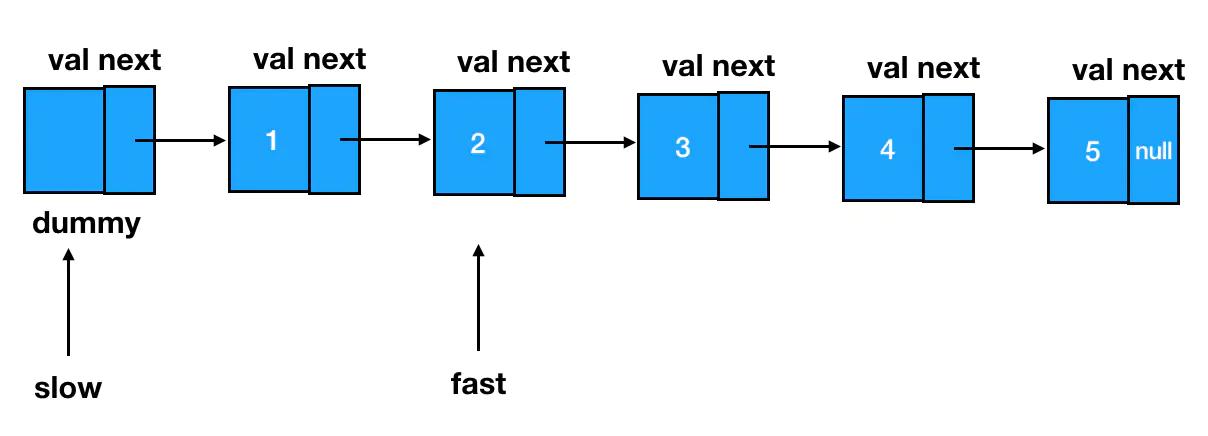
然后，快慢指针一起前进，当快指针前进到最后一个结点处时，两个指针再一起停下来：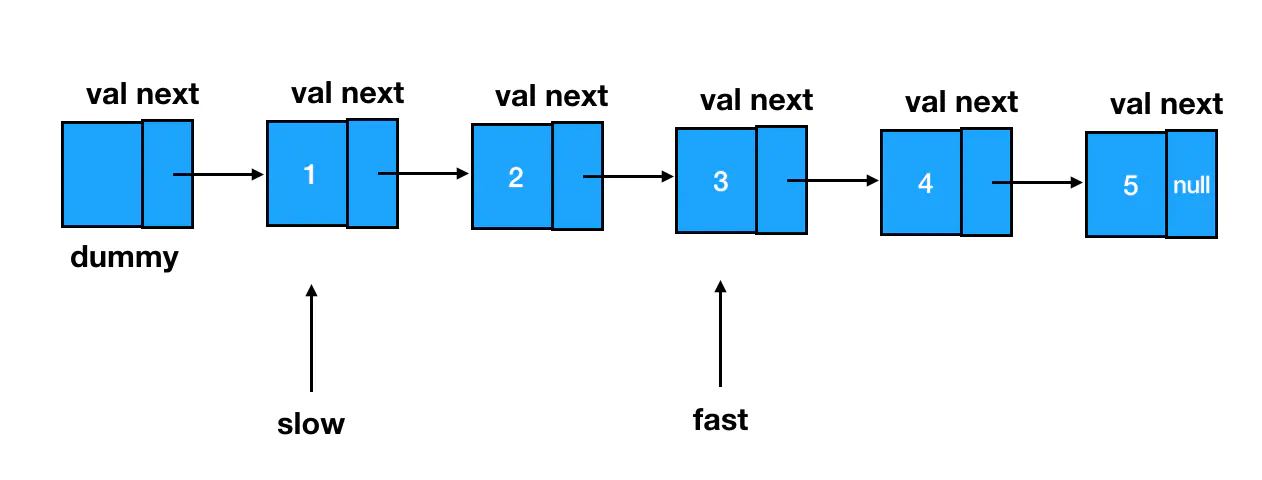


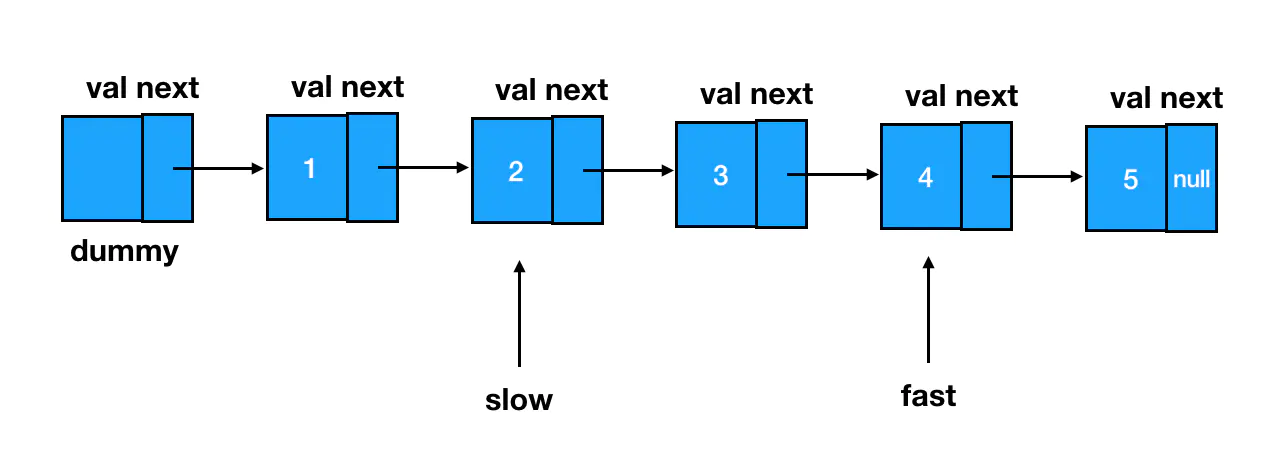
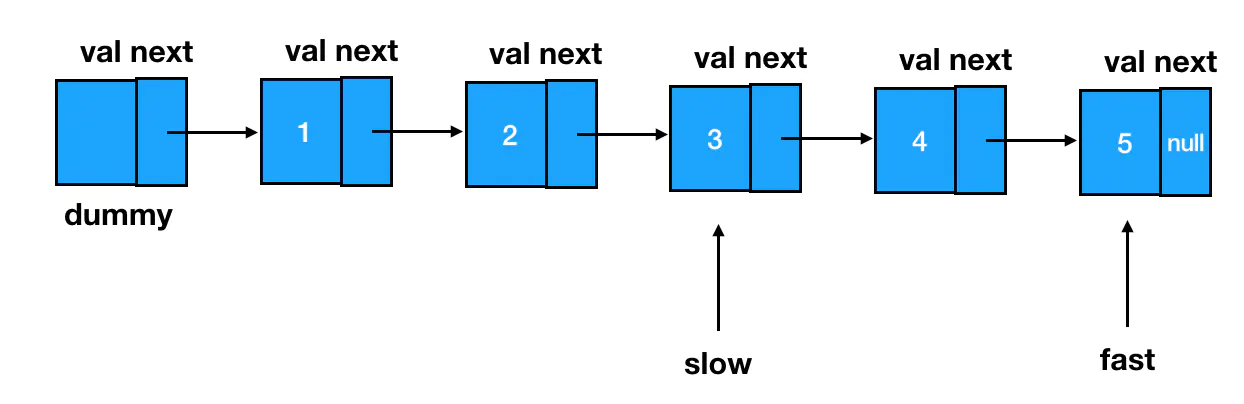此时，慢指针所指的位置，就是倒数第 n 个结点的前一个结点：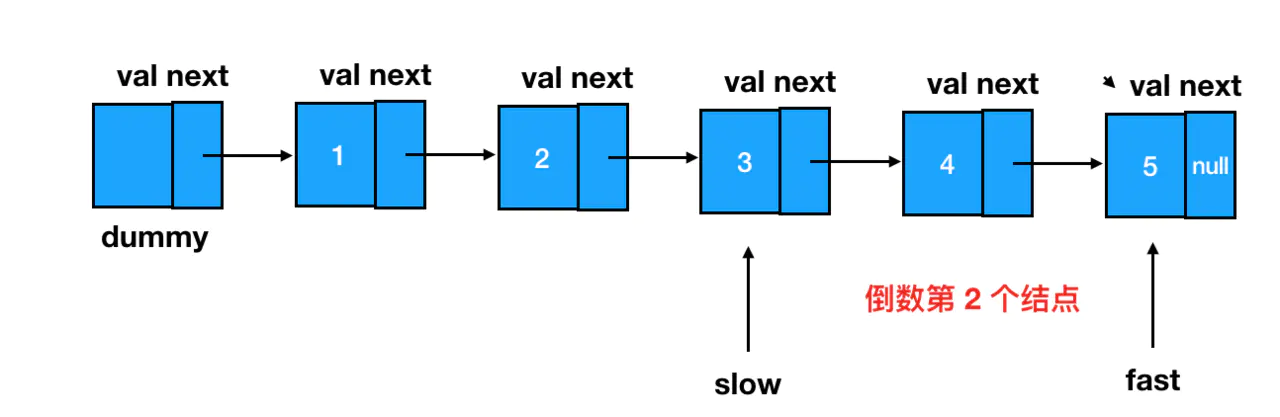
我们基于这个结点来做删除，可以说是手到擒来：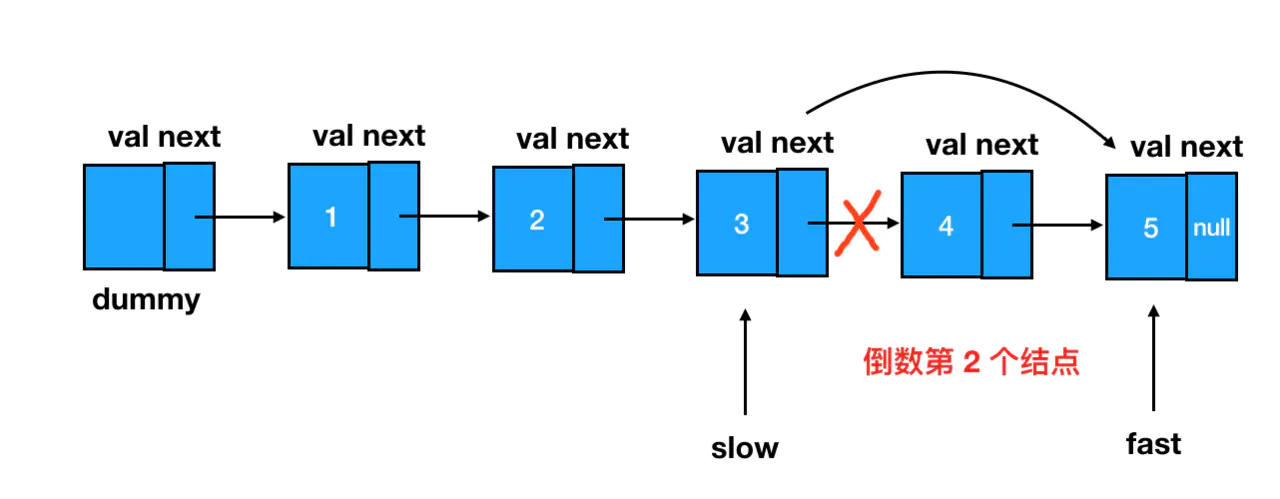

到这里，我们总结一下：
链表删除问题中，若走两次遍历，我们做了两件事：
1.求长度
2.做减法，找定位。
若用快慢指针，我们其实是把做减法和找定位这个过程给融合了。通过快指针先行一步、接着快慢指针一起前进这个操作，巧妙地把两个指针之间的差值保持在了“n”上（用空间换时间，本质上其实就是对关键信息进行提前记忆，这里咱们相当于用两个指针对差值实现了记忆），这样当快指针走到链表末尾（第 len 个）时，慢指针刚好就在 len - n 这个地方稳稳落地。

编码实现

/**
 * @param {ListNode} head
 * @param {number} n
 * @return {ListNode}
 */
const removeNthFromEnd = function(head, n) {
    // 初始化 dummy 结点
    const dummy = new ListNode()
    // dummy指向头结点
    dummy.next = head
    // 初始化快慢指针，均指向dummy
    let fast = dummy
    let slow = dummy
    // 快指针闷头走 n 步
    while(n!==0){
        fast = fast.next
        n--
    }
    // 快慢指针一起走
    while(fast.next){
        fast = fast.next
        slow = slow.next
    }
    // 慢指针删除自己的后继结点
    slow.next = slow.next.next
    // 返回头结点
    return dummy.next
};

多指针法——链表的反转

完全反转一个链表

真题描述：定义一个函数，输入一个链表的头结点，反转该链表并输出反转后链表的头结点。 示例:

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

思路解读

这道题虽然是一道新题，但你要说你完全没思路，我真的哭了orz。老哥，我真想把这句话刻你显示器上——处理链表的本质，是处理链表结点之间的指针关系。
我啥也不说，就给你一张链表的结构图：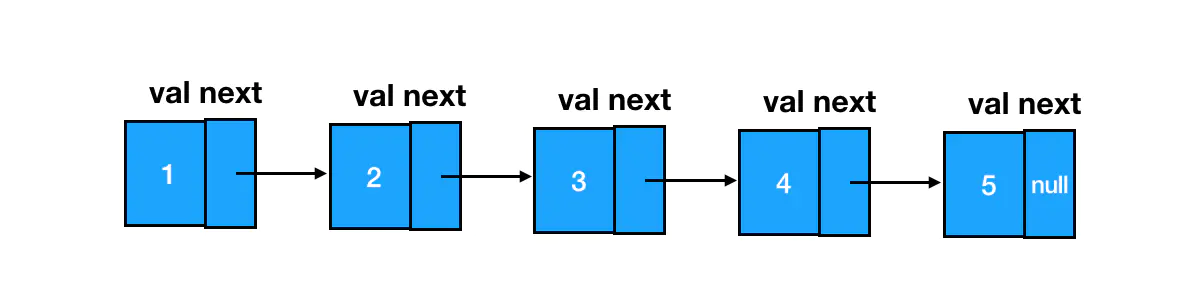

来，你告诉我，我如何把这货颠倒个顺序呢？
是不是想办法把每个结点 next 指针的指向给反过来就行了：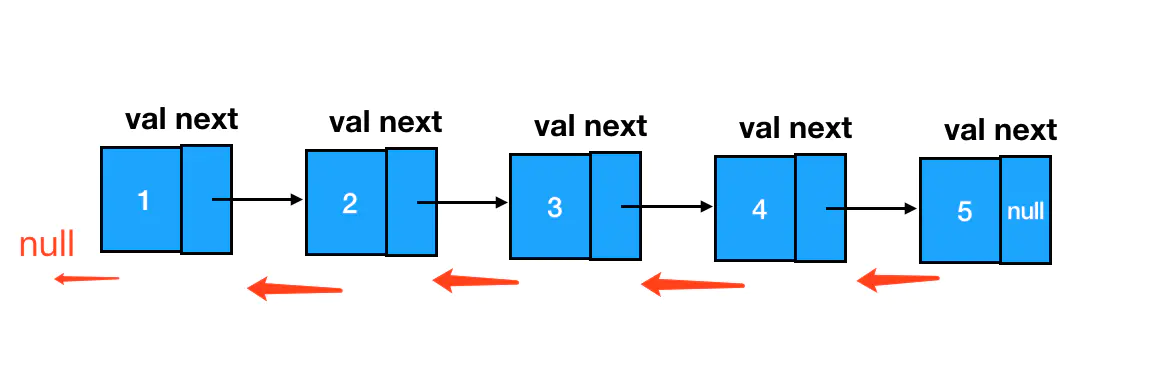

你只要能想到这一步，就说明你对链表操作类题目已经有了最关键的感知，给你双击666~
接下来我们需要琢磨的是如何去反转指针的指向，这里我们需要用到三个指针，它们分别指向目标结点（cur）、目标结点的前驱结点（pre）、目标结点的后继结点（next）。这里咱们随便找个结点来开刀：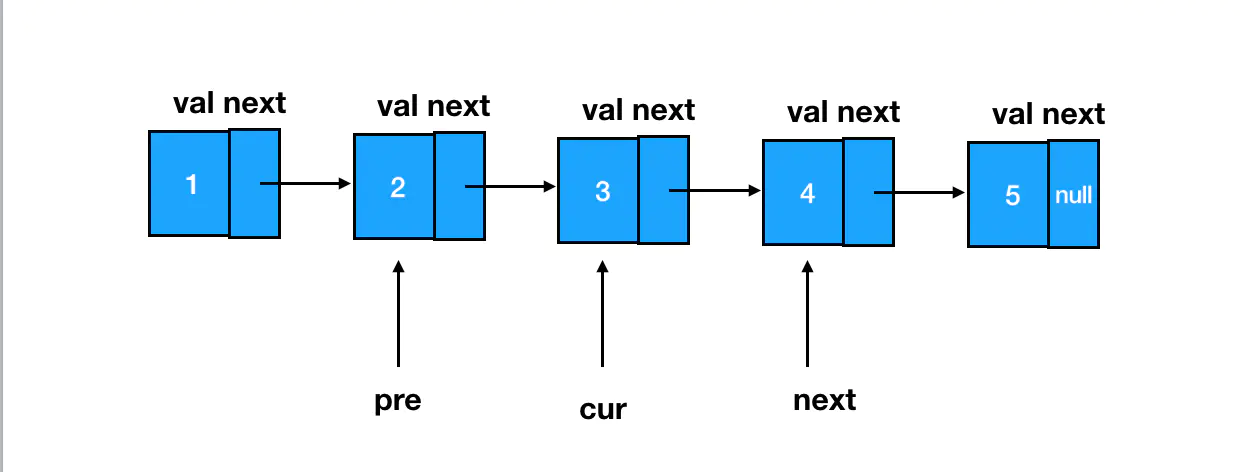

这里我只需要一个简单的cur.next = pre，就做到了 next 指针的反转：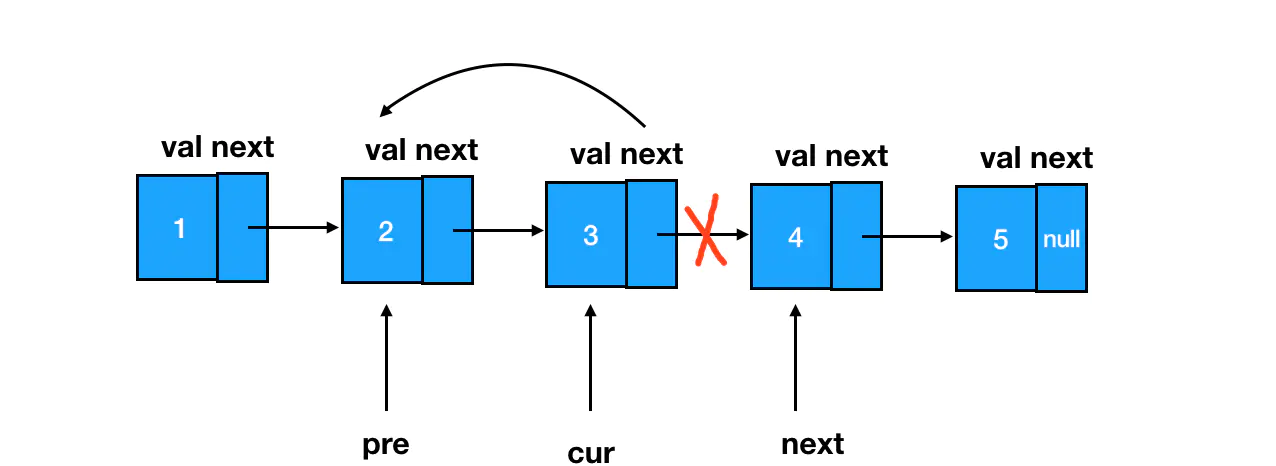

有同学会说：那 next 不是完全没用到吗？
当然有用，你瞅瞅，咱们反转完链表变成啥样了：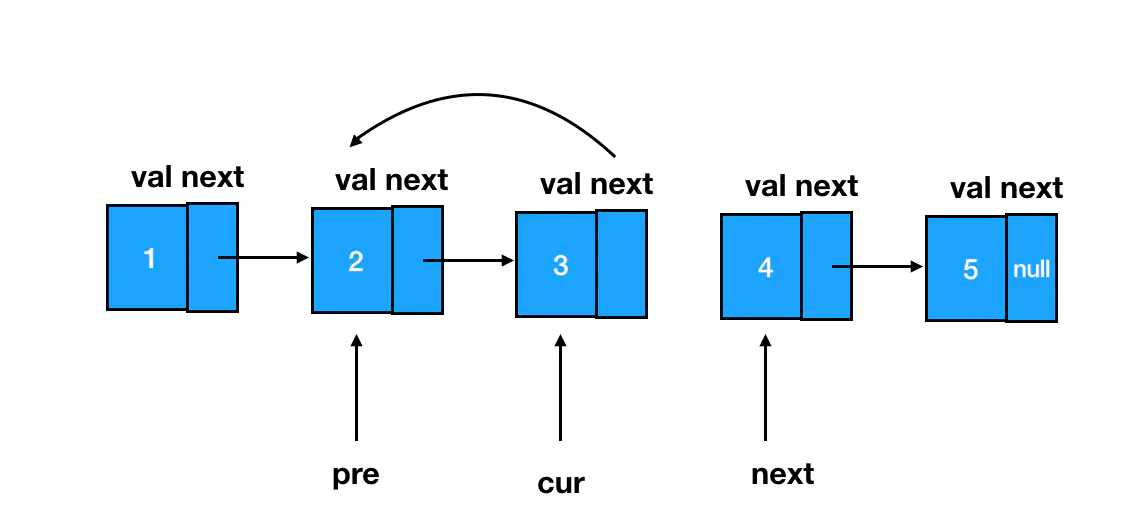

这会儿我要是不用 next 给你指着 cur 原本的后继结点，你上哪去定位下一个结点呢？遍历都没法继续了嗷。
咱们从第一个结点开始，每个结点都给它进行一次 next 指针的反转。到最后一个结点时，整个链表就已经被我们彻底反转掉了。

编码实现

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
const reverseList = function(head) {
    // 初始化前驱结点为 null
    let pre = null;
    // 初始化目标结点为头结点
    let cur = head;
    // 只要目标结点不为 null，遍历就得继续
    while (cur !== null) {
        // 记录一下 next 结点
        let next = cur.next;
        // 反转指针
        cur.next = pre;
        // pre 往前走一步
        pre = cur;
        // cur往前走一步
        cur = next;
    }
    // 反转结束后，pre 就会变成新链表的头结点
    return pre
};

局部反转一个链表

反转链表真是座金矿，反转完整体反转局部，反转完局部还能每 k 个一组花式反转（最后这个略难，我们会放在真题训练环节来做）。虽然难度依次进阶，但只要把握住核心思想就没问题，下面咱们来看看如何反转局部：

真题描述：反转从位置 m 到 n 的链表。请使用一趟扫描完成反转。 说明:

1 ≤ m ≤ n ≤ 链表长度。

示例:

输入: 1->2->3->4->5->NULL, m = 2, n = 4
输出: 1->4->3->2->5->NULL

思路解读

我们仍然是从指针反转来入手：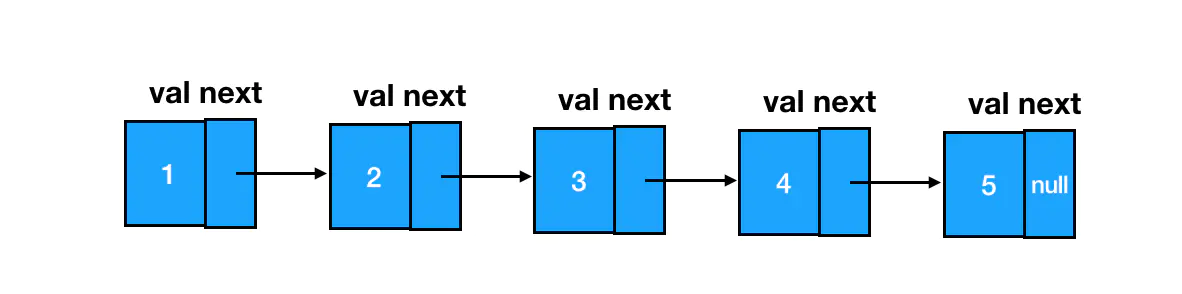

按照题中的示例，假如我们需要反转的是链表的第 2-4 之间的结点，那么对应的指针逆序后会是这个样子：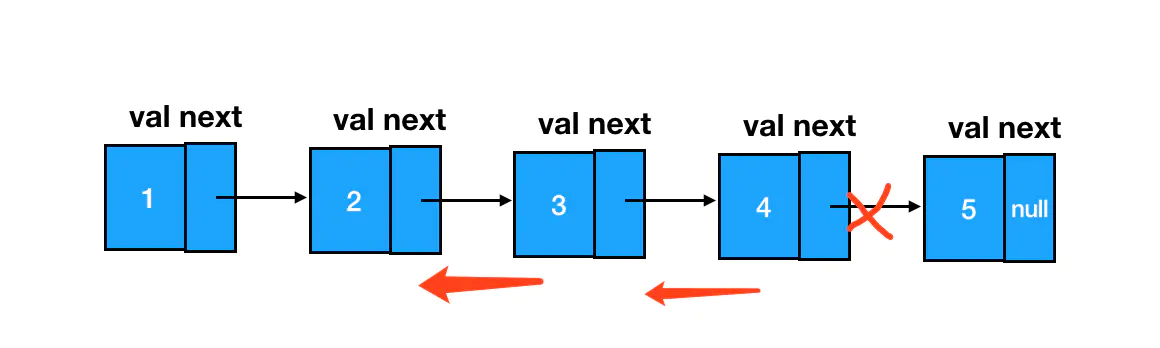

4指3，3指2，这都没问题，关键在于，如何让1指向4、让2指向5呢？这就要求我们在单纯的重复“逆序”这个动作之外，还需要对被逆序的区间前后的两个结点做额外的处理：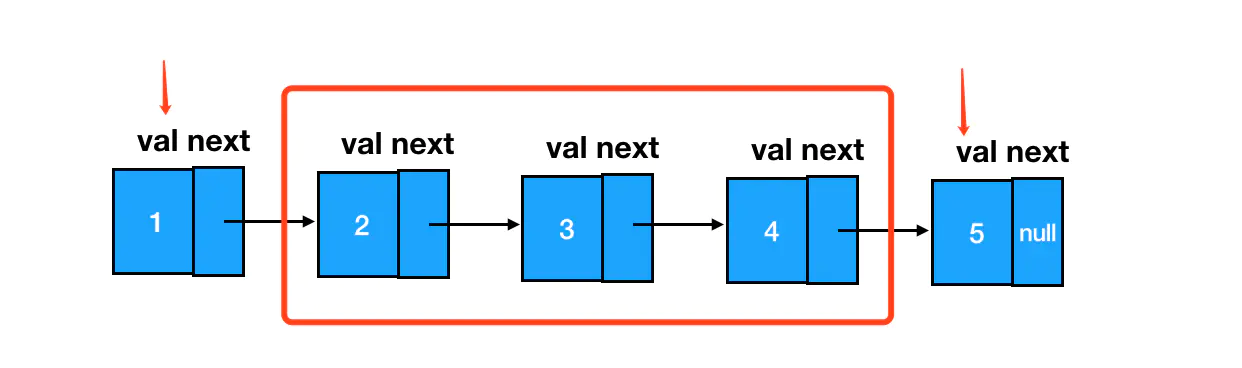

由于我们遍历链表的顺序是从前往后遍历，那么为了避免结点1和结点2随着遍历向后推进被遗失，我们需要提前把1结点缓存下来。而结点5就没有这么麻烦了：随着遍历的进行，当我们完成了结点4的指针反转后，此时 cur 指针就恰好指在结点5上：

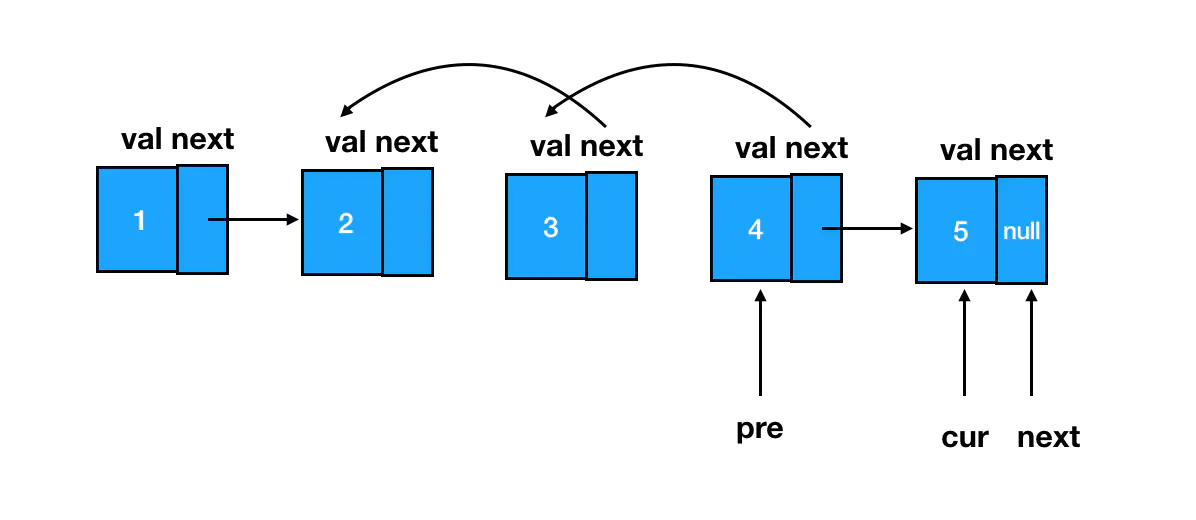
此时我们直接将结点2的 next 指针指向 cur、将结点1的 next 指针指向 pre 即可。

编码实现

/**
 * @param {ListNode} head
 * @param {number} m
 * @param {number} n
 * @return {ListNode}
 */
// 入参是头结点、m、n
const reverseBetween = function(head, m, n) {
    // 定义pre、cur，用leftHead来承接整个区间的前驱结点
    let pre,cur,leftHead
    // 别忘了用 dummy 嗷
    const dummy = new ListNode()  
    // dummy后继结点是头结点
    dummy.next = head
    // p是一个游标，用于遍历，最初指向 dummy
    let p = dummy  
    // p往前走 m-1 步，走到整个区间的前驱结点处
    for(let i=0;i<m-1;i++){
        p = p.next
    }
    // 缓存这个前驱结点到 leftHead 里
    leftHead = p
    // start 是反转区间的第一个结点
    let start = leftHead.next  
    // pre 指向start
    pre = start
    // cur 指向 start 的下一个结点
    cur = pre.next
    // 开始重复反转动作
    for(let i=m;i<n;i++){
        let next = cur.next
        cur.next = pre
        pre = cur
        cur = next
    }
    //  leftHead 的后继结点此时为反转后的区间的第一个结点
    leftHead.next = pre
    // 将区间内反转后的最后一个结点 next 指向 cur
    start.next=cur
    // dummy.next 永远指向链表头结点
    return dummy.next
};

小贴士：楼上的两道反转题目，都可以用递归来实现，你试试？