15 | 场景化解读：递归与回溯思想在真题中的应用

根据我深耕技术写作多年的经验，很多同学一看到标题里有“思想”两个字，就会觉得接下来要讲的一定是一个非常复杂的“高大上”理论，于是他会先给自己箍上一个“我一定学不会”的紧箍咒，接着心里就开始打退堂鼓了。这样的同学在和算法正面交锋之前，就先被自己内心的恐惧击垮了，实在可惜。

站在讲解者的角度来说，我确实不会先给大家画个饼，说这玩意儿有多么多么简单——这是一个非常不负责任的承诺。因为对于初学者来说，没有什么是简单的，从不会到会本来就是一个过程。况且，你现在学的是不少前端er都不肯学/学不动的算法，这本就不是一个轻松的挑战。但既然走到了这一步，不管你这会儿心里有多慌，我都希望你可以坚持一下、读读看，你会发现这玩意儿真的不是玄学——它真的很香。

如何学好这一节

不可否认，在一些传统教材里，谈及“思想”必定会有大段理论文字的堆砌，这也是很多同学学完数据结构直接放弃学习算法思想的重要原因。

但站在面试的角度来看，算法相关的考察几乎不存在“背知识点”这种形式，更多还是看你能不能把题做出来。算法思想是抽象的，题目却是具体的。我们常说“以题为纲”，其目的就是帮助大家站在具体去理解抽象。

本节我们先不用纠结什么是递归、什么是回溯，而是直接来做一道题，从题中去认识所谓的“思想”。

通过本节的学习，我希望大家能够认识到，“思想”并不是一坨剪不断理还乱、学了只能用来吹水的虚无概念。“思想”本质上就是套路，而且是普适性非常强的套路，它有着大量的对口问题。搞定了它，就搞定了一大波面试题——爽不爽？要想爽这一把，就不要轻易撤退。

关键套路初相见：全排列问题

题目描述：给定一个没有重复数字的序列，返回其所有可能的全排列。

示例：
输入: [1,2,3] 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

思路分析

“全排列”是高中数学里的一个概念，这里先带大家复习一下：

从n个不同元素中任取m（m≤n）个元素，按照一定的顺序排列起来，叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。

不过就算你已经完全忘了“全排列”到底是一个什么样的数学概念，也没有关系。结合题目描述和示例，我们依然可以分析出这道题想让我们做的事情：拿到一个 n 个数的数组作为入参，穷举出这 n 个数的所有排列方式。

哎？等等，我好像看到一个熟悉的词眼——穷举！楼上是不是说了穷举？我们最近还在哪里见过穷举？是不是在上一节？上一节的哪个位置？DFS 对不对？DFS 用什么实现比较好？递归！好，来得早不如来得巧，我现在就决定用递归来做这个题。

如果你的脑回路暂时没有反应出来上面这些知识点之间的关联关系，也不要着急。新手上路，这很正常。    
做完下面一系列的题目之后，我会跟大家介绍这类题目的关键特征，到时候会有更直白的套路可以用。现在先不要慌，跟着我的思路往下走，好好敲代码

怎么做呢？大家仔细想想，在这个变化的序列中，不变的是什么——是不是坑位的数量？拿示例来说，不管我怎么调整数字的顺序，它们都只能围着这 3 个坑打转。当我们感到变化难以把握时，不如尝试先从不变的东西入手。这里我把坑位给大家画出来：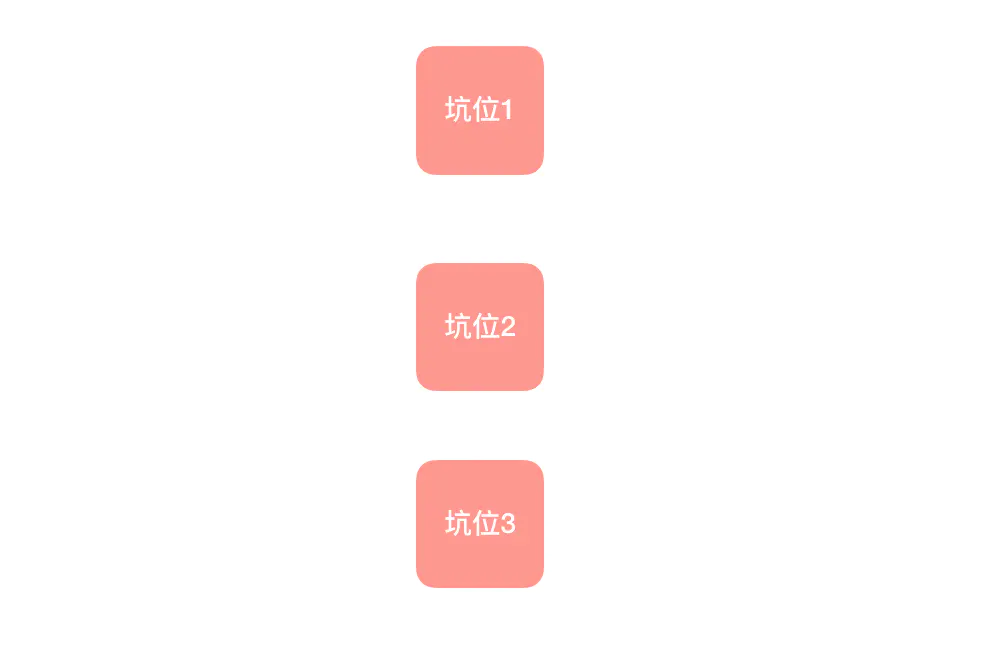


现在问题变成了，我手里有 3 个数，要往这 3 个坑里填，有几种填法？我们一个一个坑来看：

• Step1:：面对第一个坑，我有3种选择：填1、填2、填3，随机选择其中一个填进去即可。
• Step2：面对第二个坑，由于 Step1 中已经分出去1个数字，现在只剩下2个选择：比如如果 Step1 中填进去的是 1，那么现在就剩下2、3；如果 Step1 中填进去的是 2，那么就剩下 1、3。
• Step3： 面对第三个坑，由于前面已经消耗了2个数字，此时我们手里只剩下 1 个数字了。所以说第 3 个坑是毫无悬念的，它只有1种可能。

我们把三个坑的情况统筹起来，那么全排列就一共有 3x2x1=6 种可能。可惜这道题问的不是全排列的可能性有多少种，而是要求你把每一种可能性都穷举出来。这其实有点类似于我们上一节玩迷宫游戏的时候，游戏规则不仅要求你回答出迷宫的通关方法有几种，还要求你列举出每一条路的路径。列举“路径”，我们首先要找到“坐标”。在这道题里，“坐标”就是每一个坑里可能填进的数字。我把它画出来，你就明白了：

root 是一个空坐标，是我们分配数字的起点。
你可以想象自己此时此刻正手握 3 个数字站在 root 这个位置上。眼前是第一个坑，这个坑向你问道：“小哥，你打算给我哪个数字呢？”
你说：“不好说，这里有 3 种可能”。第一个坑里可以填的数字，对应的是以下三种情况：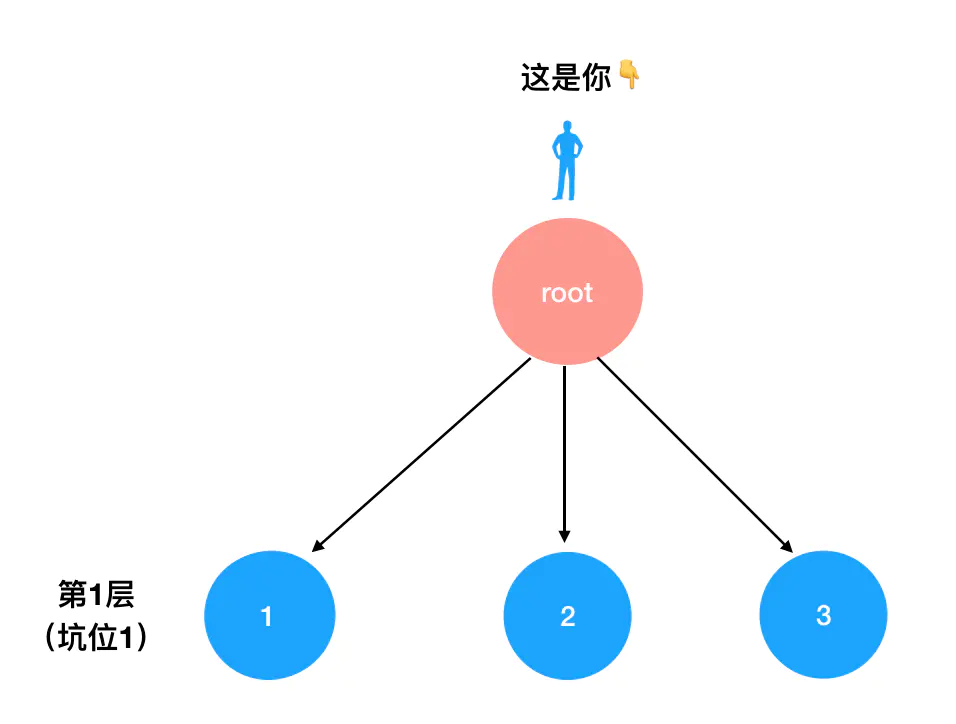


接着，你走到了第二个坑。第二个坑问你：“小哥，你打算给我哪个数字呢？”。
你仔细想想，说：“不好说，这要看我给了 1 号坑哪个数字。但可以确定的是，不管我给了 1 号坑哪个数字，到你这里的时候，都只有 2 个数字可选了”。基于 1 号坑的分配结果，2 号坑分别有以下可能：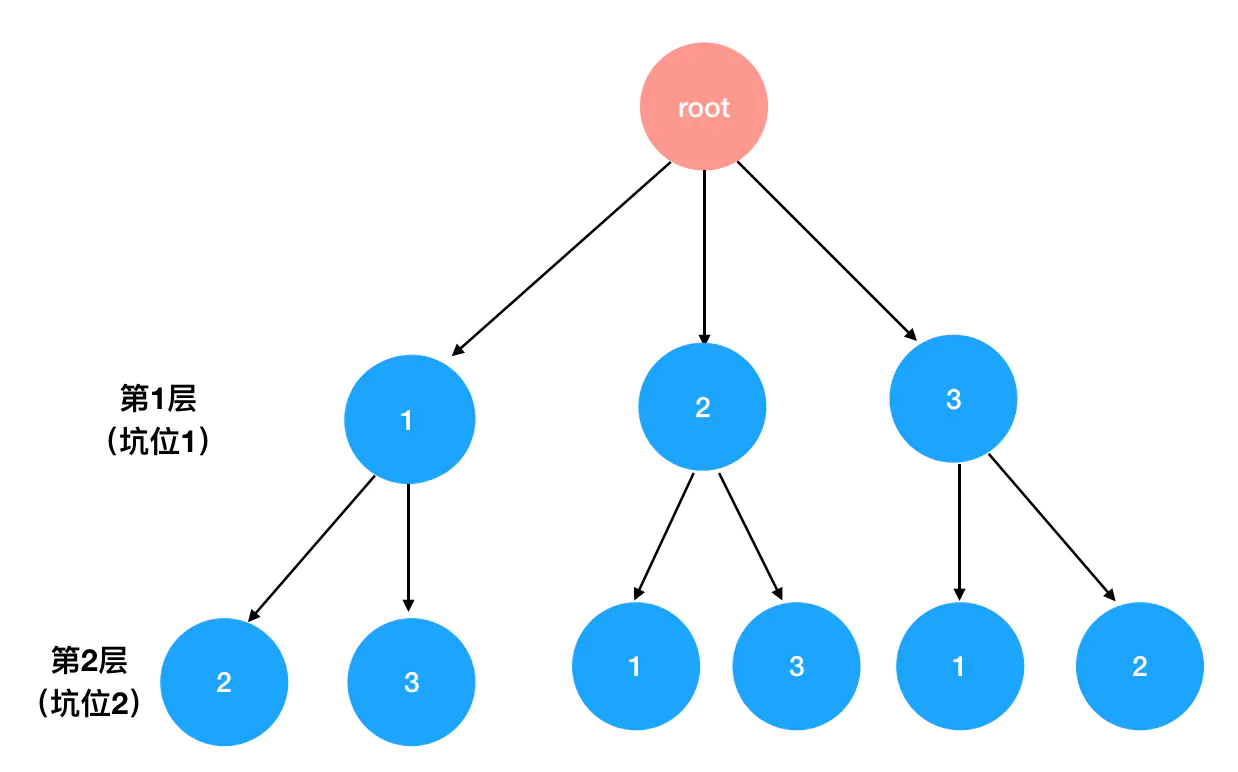

终于，你走到了第三个坑。此时，你手里只剩下 1 个数，还没等第 3 个坑问你要，你就对它说：“哥，别挑了，我就剩一个了，你没得选”。说着，你把 1 号坑和 2 号坑挑完剩下的最后 1 个数给了 3 号坑：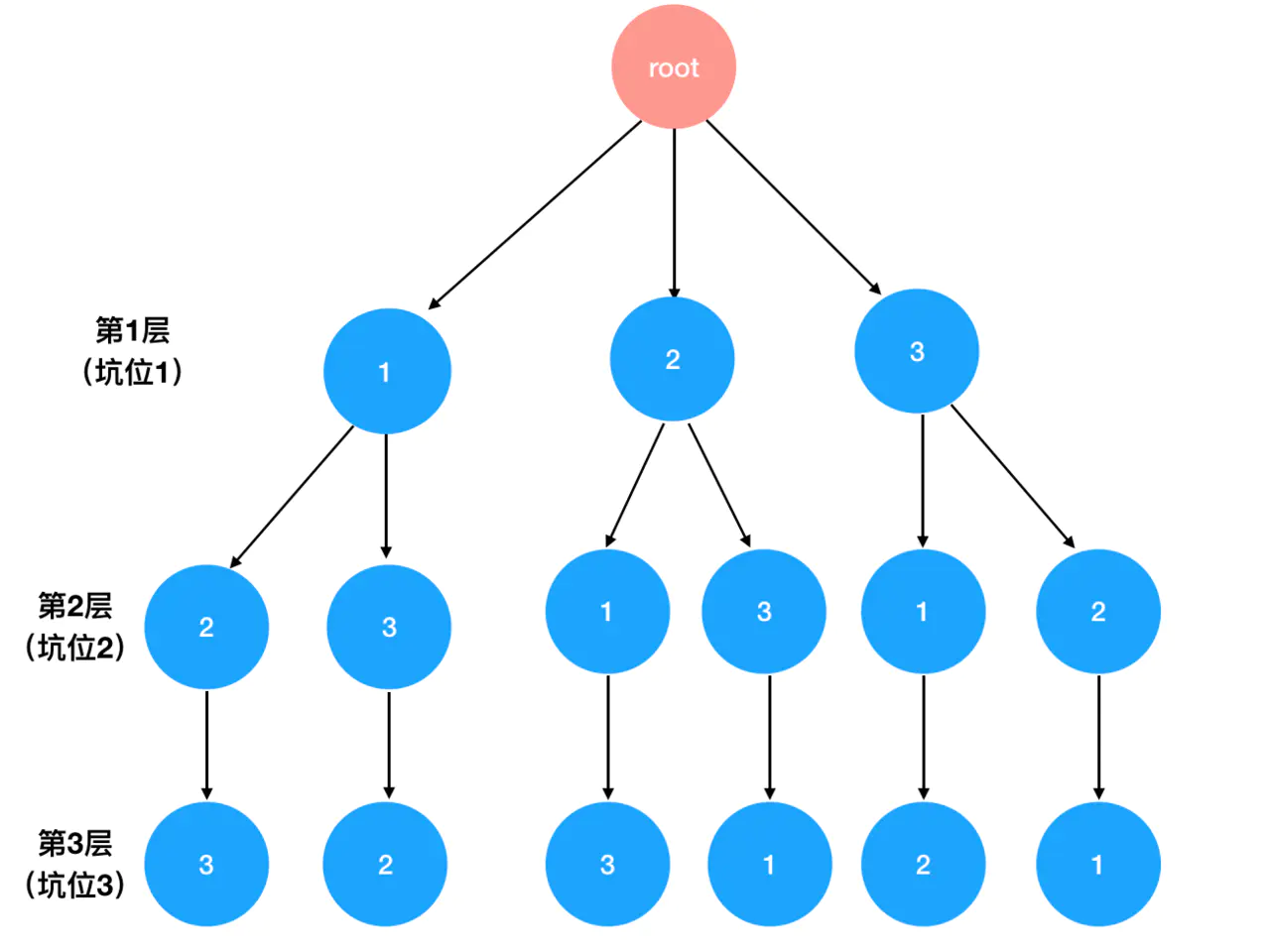


有没有发现，不知不觉中，我们构造出了一个树结构。
从这个树结构里我们可以清晰地看出，全排列的所有可能性：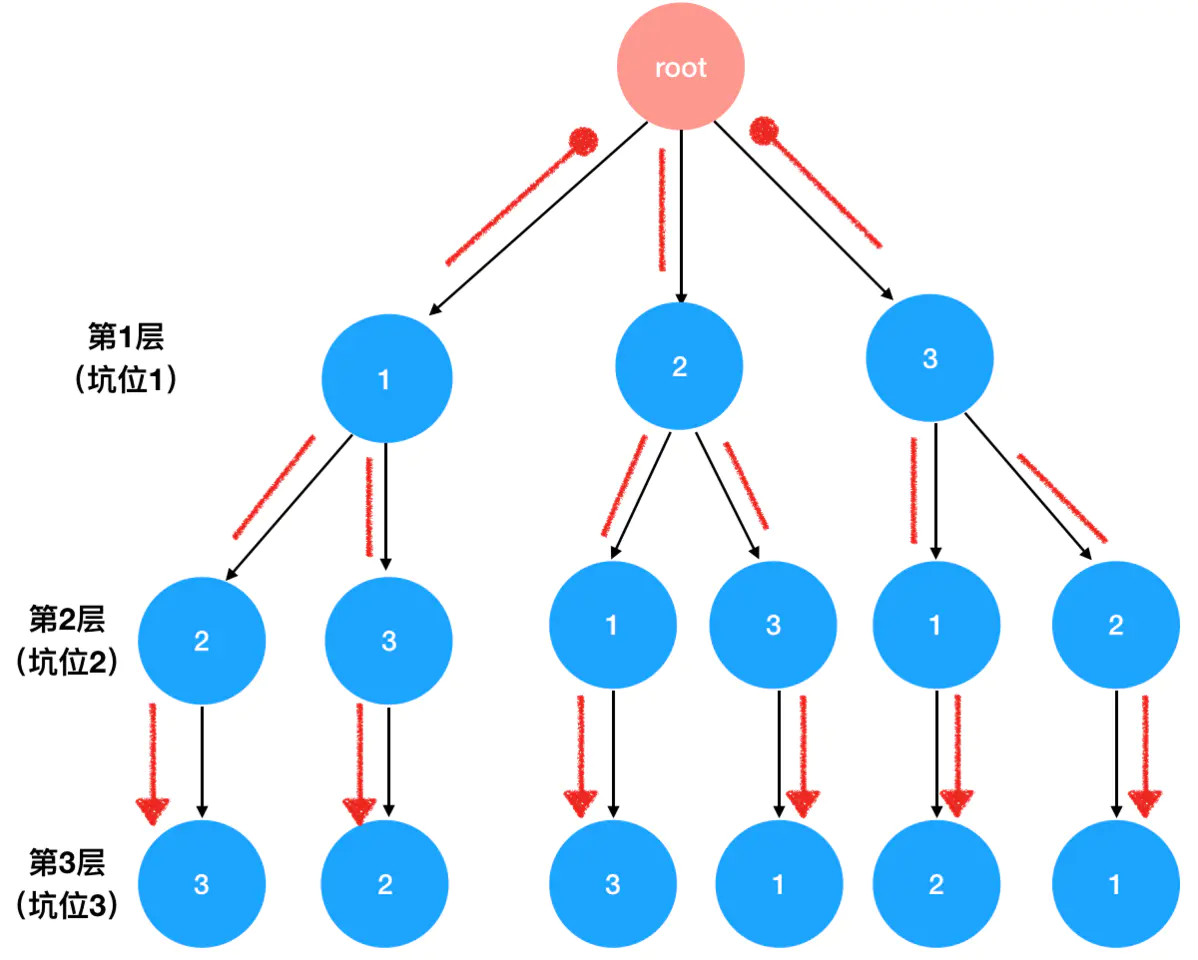

图中以圆点为起点，以箭头为终点，起点和终点之间就是一个完整的排列。

我们的思维路径是一个树结构，但这并不意味着我们需要真的在编码的时候去构造一棵树出来。回忆一下上一节，我们走迷宫的各种路径组合起来，是不是也是一个树结构？走迷宫时我们没有构造树，这里也不需要构造树。需要什么？需要递归！

即便不联想咱们刚刚学过的 DFS 知识点，这道题的解答思路中也有一个非常关键的特征在提醒你往递归去想，那就是重复。

这里给大家一个思维工具：以后只要分析出重复的逻辑（排除掉类似数组遍历这种简单粗暴的重复），你都需要把递归从你的大脑内存里调度出来、将其列为“可以一试”的解法之一；只要想到递归，立刻回忆我们上一节讲的 DFS 思想、然后尝试套我们这一节末尾教给大家的解题模板。这个脑回路未必 100% 准确，但确实有极高的成功概率——题，是有规律的。这，就是规律之一。

在以上的“填坑”过程中，我们重复地做了以下事情：

1. 检查手里剩下的数字有哪些
2. 选取其中一个填进当前的坑里

在第 5 节初识递归时，大家已经知道“重复”的内容，就是递归式。

这个重复递归式的动作一直持续到了最后一个数字也被填进坑里为止——“重复”的终点，就是递归边界。

这里大家当然也可以借鉴遍历二叉树的经验 ，通过判断数组的可选数字是否为空，来决定当前是不是走到了递归边界。但是这道题其实可以做得更简单：坑位的个数是已知的，我们可以通过记录当前坑位的索引来判断是否已经走到了边界：比如说示例中有 n 个坑，假如我们把第 1 个坑的索引记为 0 ，那么索引为 n-1 的坑就是递归式的执行终点，索引为 n 的坑（压根不存在）就是递归边界。

递归的编码实现，无非是把我们上面描述过的递归式和递归边界翻译成代码：

编码实现

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
// 入参是一个数组
const permute = function(nums) {
  // 缓存数组的长度
  const len = nums.length
  // curr 变量用来记录当前的排列内容
  const curr = []
  // res 用来记录所有的排列顺序
  const res = []
  // visited 用来避免重复使用同一个数字
  const visited = {}
  // 定义 dfs 函数，入参是坑位的索引（从 0 计数）
  function dfs(nth) {
      // 若遍历到了不存在的坑位（第 len+1 个），则触碰递归边界返回
      if(nth === len) {
          // 此时前 len 个坑位已经填满，将对应的排列记录下来
          res.push(curr.slice())
          return 
      }
      // 检查手里剩下的数字有哪些
      for(let i=0;i<len;i++) {
          // 若 nums[i] 之前没被其它坑位用过，则可以理解为“这个数字剩下了”
          if(!visited[nums[i]]) {
              // 给 nums[i] 打个“已用过”的标
              visited[nums[i]] = 1
              // 将nums[i]推入当前排列
              curr.push(nums[i])
              // 基于这个排列继续往下一个坑走去
              dfs(nth+1) 
              // nums[i]让出当前坑位
              curr.pop()
              // 下掉“已用过”标识
              visited[nums[i]] = 0
          }
      }
  }
  // 从索引为 0 的坑位（也就是第一个坑位）开始 dfs
  dfs(0)
  return res
};

小贴士

上面这坨代码里，有两个点需要大家格外注意，它们将会成为我们以后做类似题目的关键技巧：

1. Map 结构 visited 的使用：填坑时，每用到一个数字，我们都要给这个数字打上“已用过”的标——避免它被使用第二次；数字让出坑位时，对应的排列和 visited 状态也需要被及时地更新掉。
2. 当走到递归边界时，一个完整的排列也到手了。将这个完整排列推入结果数组时，我们用了 res.push(curr.slice()) 而不是简单的 res.push(curr) 。为什么这样做？因为全局只有一个唯一的 curr ， curr 的值会随着 dfs 的进行而不断被更新。 slice 方法的作用是帮助我们拷贝出一个不影响curr正本的副本，以防直接修改到curr的引用。

带着全排列问题教会我们的解题思路和编码技巧，我们再来看另一个类型的题目——组合问题。

组合问题：变化的“坑位”，不变的“套路”

题目描述：给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。 说明：解集不能包含重复的子集。 示例: 输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]

思路分析

见到这道题，大家第一反应会是什么？吸取了上一道题的经验，这道题我们应该想到的是：穷举出现了，大概率会用到 DFS。
只要用到 DFS，就不得不想到树形思维方式，进而不得不思考递归式和递归边界的问题。在这个思考的过程中，最重要的一环就是对“坑位”的定位和分析。
从上一道题中，我们不难看出，“坑位”对应的就是树形逻辑中树的某一层，“坑位数”往往意味着递归边界的限制条件。

找“坑位”的思路也是具有规律的：“坑位”往往是那些不会变化的东西。在上一道题中，排列的顺序是变化的，而每个排列中数字的个数却是不变的，因此数字的个数就对应“坑位”的个数；在这道题中，每个组合中数字的个数是不确定的，不变的东西变成了可以参与组合的数字，变化的东西则是每个数字在组合中的存在性。因此我们的思路可以调整为，从每一个数字入手，讨论它出现或者不出现的情况。
换汤不换药，这里我们仍然采取树形思维模型：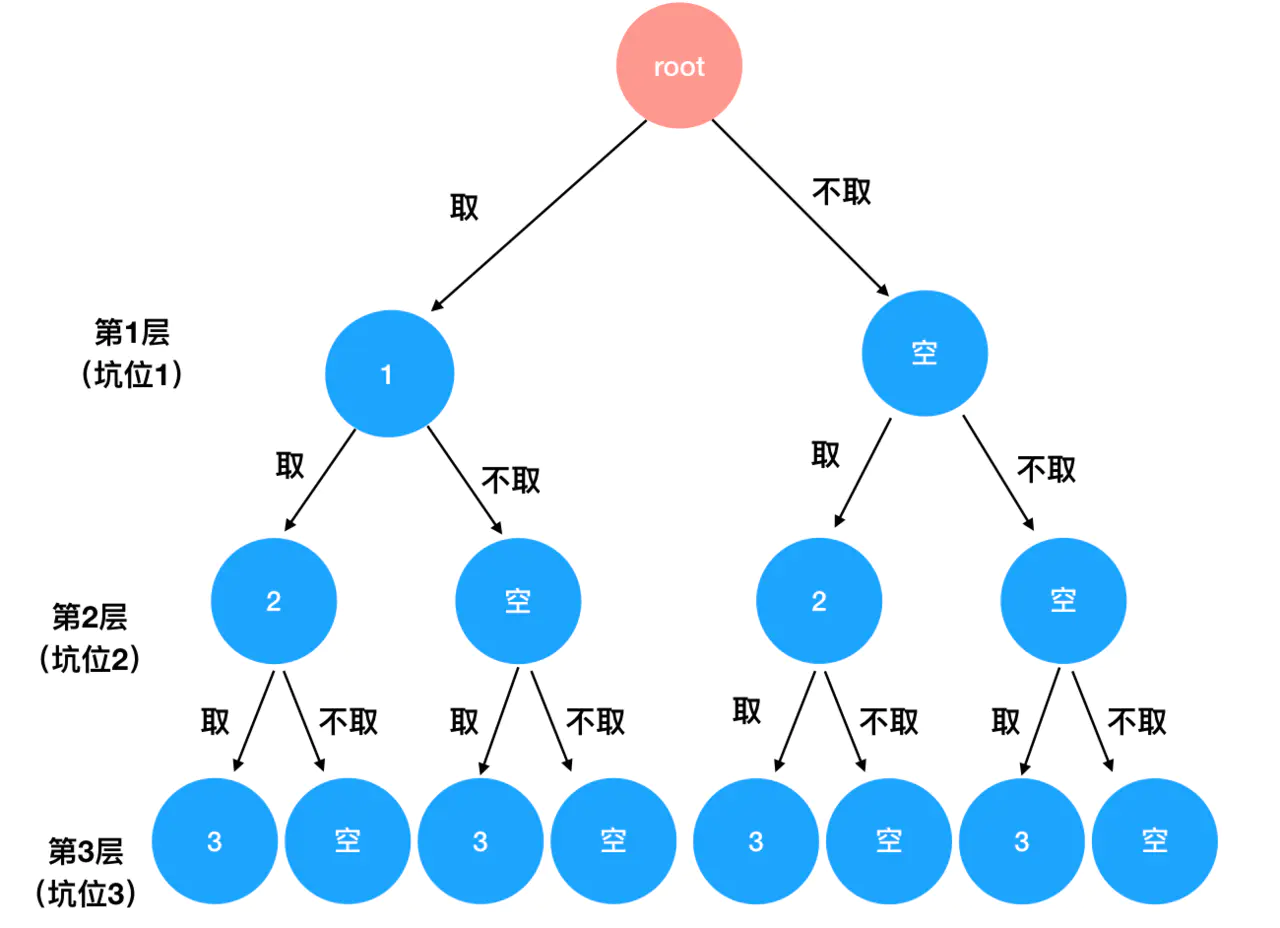

为了使存在性凸显得更具体，这里我直接把树形结构中每一层对应的可能组合给大家列出来：

root                                            []                  
数字1——第一层                     1                                   []
数字2——第二层            [1,2]            [1]                   [2]         []
数字3———第三层    [1,2,3]     [1,2]  [1,3]   [1]           [2,3]   [2]   [3]  []

从 root 出发，每一个数字对应树的一层，存在或不存在对应树的两个分叉。从第一层到第三层，我们得到的所有完整路径，就是 3 个数的所有可能的组合形式。

我们分析一下这个过程中的递归式与递归边界：

• 递归式：检查手里剩下的数字有哪些（有没有发现和上一道题的递归式是一样的，因为两道题都强调了数字不能重复使用），选取其中一个填进当前的坑里、或者干脆把这个坑空出来（这里就体现出了和上一道题的区别，这道题强调的是存在性而非顺序）。
• 递归边界：组合里数字个数的最大值。拿示例来说，只给了 3 个数，因此组合里数字最多也只有 3 个，超过 3 个则视为触碰递归边界。

按照这个思路，可以编码如下：

编码实现

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
// 入参是一个数组
const subsets = function(nums) {
    // 初始化结果数组
    const res = []   
    // 缓存数组长度
    const len = nums.length
    // 初始化组合数组
    const subset = []
    // 进入 dfs
    dfs(0)  
    // 定义 dfs 函数，入参是 nums 中的数字索引
    function dfs(index) {
        // 每次进入，都意味着组合内容更新了一次，故直接推入结果数组
        res.push(subset.slice())
        // 从当前数字的索引开始，遍历 nums
        for(let i=index;i<len;i++) {
            // 这是当前数字存在于组合中的情况
            subset.push(nums[i]) 
            // 基于当前数字存在于组合中的情况，进一步 dfs
            dfs(i+1)
            // 这是当前数字不存在与组合中的情况
            subset.pop()
        }
    }
    // 返回结果数组
    return res 
};

编码复盘

这道题和上一道题的基本思路高度一致，但是在实现上有些差别。对初学者来说，即便是非常微小的变化也有可能引起困惑。因此，我在这里针对编码部分变化的内容作进一步讲解：

• 递归式的变化：在上一道题中，我们检查一个数字是否可用的依据是它是否已被纳入当前排列（ visited 值是否为 1），而这道题中，并不存在一个类似 visited 一样的标记对象。取而代之的，是每次直接以 index 作为了索引起点。这是因为，在排列场景下，一个元素可能出现在任何坑位里；而在组合场景下，坑位的选择逻辑发生了变化，坑位和元素是一一对应的。因此讨论完一个坑位的取舍后，一个元素的取舍也相应地讨论完毕了，直接跳过这个元素的索引往下走即可。
• 递归边界的变化：这道题中，并没有显式的 return 语句来标示递归边界的存在。这个边界的判定被 for 语句偷偷地做掉了： for 语句会遍历所有的数字，当数字遍历完全时，也就意味着递归走到了尽头。
  

限定组合问题：及时回溯，即为“剪枝”

题目描述：给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。 示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]

思路分析

这是一道复杂化的组合问题，它追加了一个限定条件——只返回 n 个数中 k 个数的组合。在普通的组合问题中，树形逻辑是这样的：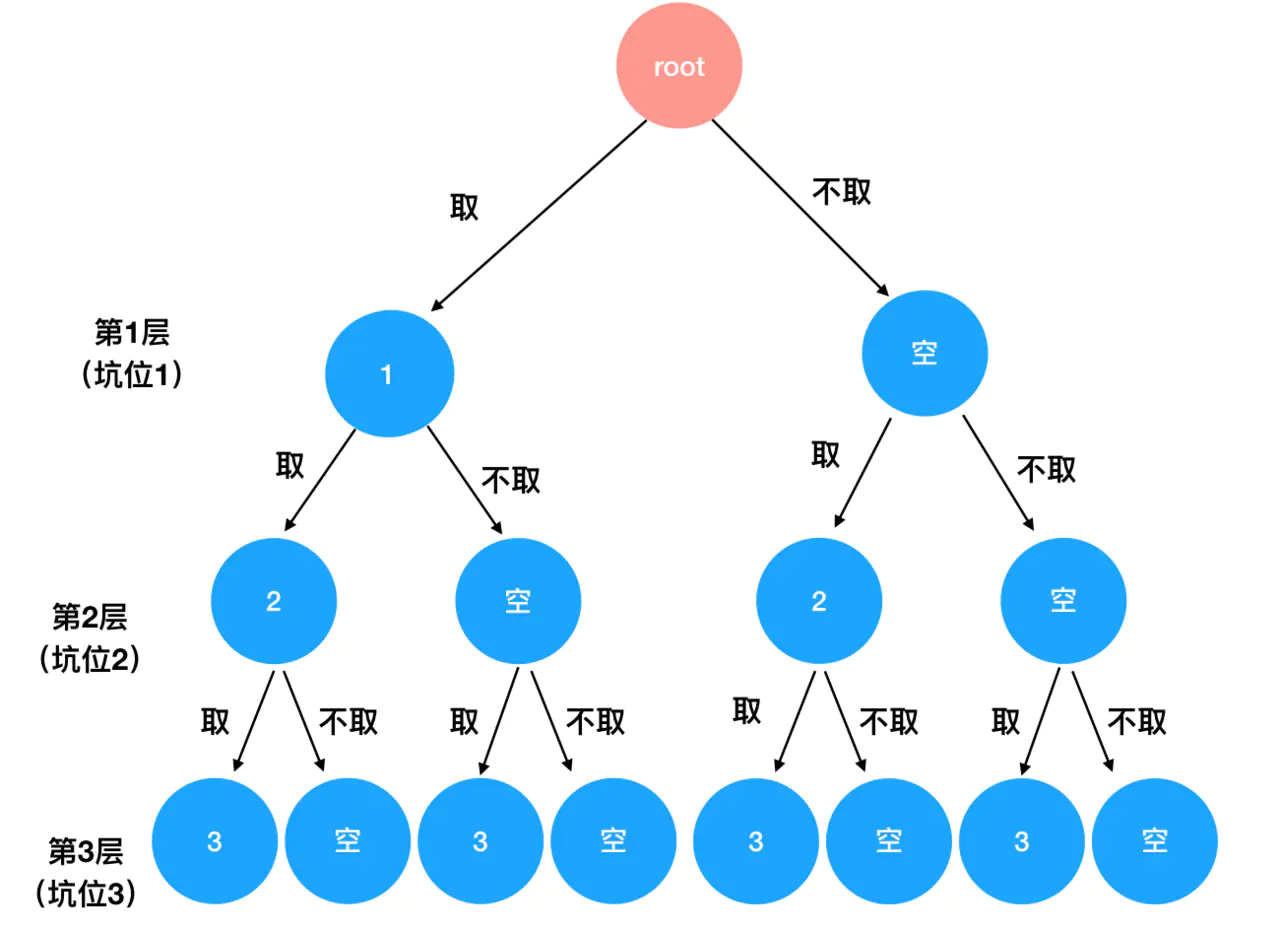

而在这道题里，树形逻辑被“截胡”了，它要求我们只输出其中的一部分。假如 n=3， k=2，那么需要输出的内容就如下图的红色箭头所示：

我们发现，只有双向箭头所指的结点组合被认为是有效结果，其它结点都被丢弃了。在寻找这三对结点组合的过程中，我们一旦找到一对，就停止继续往深处搜索，这就意味着一些结点压根没有机会被遍历到。

这其实就是“剪枝”的过程——在深度优先搜索中，有时我们会去掉一些不符合题目要求的、没有作用的答案，进而得到正确答案。这个丢掉答案的过程，形似剪掉树的枝叶，所以这一方法被称为“剪枝”。

在这道题中，要做到剪枝，我们需要分别在组合问题的递归式和递归边界上动手脚：

• 递归式：普通组合问题，每到一个新的坑位处，我们都需要对组合结果数组进行更新；这道题中，当且仅当组合内数字个数为 k 个时，才会对组合结果数组进行更新。
• 递归边界：只要组合内数字个数达到了 k 个，就不再继续当前的路径往下遍历，而是直接返回。

基于这两个改造点，我们可以编码如下：

编码实现

/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
const combine = function(n, k) {
   // 初始化结果数组
    const res = []   
    // 初始化组合数组
    const subset = []
    // 进入 dfs，起始数字是1
    dfs(1)  
    // 定义 dfs 函数，入参是当前遍历到的数字
    function dfs(index) {
        if(subset.length === k) {
            res.push(subset.slice())
            return 
        }
        // 从当前数字的值开始，遍历 index-n 之间的所有数字
        for(let i=index;i<=n;i++) {
            // 这是当前数字存在于组合中的情况
            subset.push(i) 
            // 基于当前数字存在于组合中的情况，进一步 dfs
            dfs(i+1)
            // 这是当前数字不存在与组合中的情况
            subset.pop()
        }
    }
    // 返回结果数组
    return res 
};

注意这道题中虽然没有直接给出一个 nums 数组，而是直接约定了数字的范围为 1-n ，但其本质仍然是一个数字集合，我们像上面这样稍微调整下取值方式即可。

概念复盘：何为“回溯”？

现在，或许你还暂时不知道何为“回溯算法”，但你其实已经实打实地在真题中对它有了具体的实践。基于这些实践，我们反过来理解一下回溯的概念：

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就 “回溯” 返回，尝试别的路径。

回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为 “回溯点”。
许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。
回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。 ——LeetCode
我们重点关注这句话：“回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。”

有没有发现，这个“回溯算法”和上一节的 DFS ，好像翻来覆去是在讲同一件事情？
实际上，这里的“回溯”二字，大家可以理解为是在强调 DFS 过程中“退一步重新选择”这个动作。这样想的话， DFS 算法其实就是回溯思想的体现。

这里顺便给大家提个醒：一些同学在平时的刷题和面试中，会因为对“回溯”的定义感到困惑，进而拼命地钻牛角尖，这样的做法是非常不可取的。
早年笔者有过一段短暂的 ACMer 生涯，彼时关于回溯，老师曾经给出过一个这样的解读：“在我们接下来要应对的题目里，有递归就会有回溯。回溯算法的特别之处，在于其对应的题目往往要求你在递归过程中求出一个确切的解”。后来笔者自己乱七八糟地读了一堆算法相关的“名著”，其中又有一本书这样定义回溯：“涉及剪枝操作的递归，我们一般称之为回溯”。

大家会发现，关于回溯算法的定义，可以说是仁者见仁、智者见智。这也是我不建议大家从概念入手去学算法的一个原因——反复纠结文字游戏，无法给你带来任何实质上的能力提升。在实际面试中，没有一个面试官会要求你默写算法的定义，他关注的一定是你的解题思路和编码内容——什么都是浮云，能把题做出来，才是王道！

递归与回溯问题——解题模板总结

做完了楼上三道典型例题，相信大家此时都有了一些微妙的感觉——这三道题的解题方法是非常相似的，是不是意味着涉及递归回溯、或者说涉及 DFS 应用的题目，都有某种共通之处呢？会不会存在某种解题套路，可以帮助我们知一解百、举一反 N 呢？
能想到这一层的老铁，我要给你双击一个巨大的 666——善于总结，积极寻找题目与题目之间的关联，尝试发掘题目中反映出来的规律，这都是非常棒的学习习惯。

对于递归回溯系列的问题，笔者自己在刷题过程中总结出了一套模板。在这套模板的引导下，笔者至今还没有在递归回溯问题上翻过车。在这里我和大家分享这套模板，同时也希望各位在身经百战之后，能够针对不同类型的问题，尝试去总结一套属于你自己的解题模板。

如何总结出一套解题模板？其实很简单，大家只需要搞清楚三个问题：

1. 什么时候用？（明确场景）
2. 为什么这样用？（提供依据）
3. 怎么用？（细化步骤）

拿这个专题来说，我给出的解题模板内容如下：

什么时候用

看两个特征：

1. 题目中暗示了一个或多个解，并且要求我们详尽地列举出每一个解的内容时，一定要想到 DFS、想到递归回溯。
2. 题目经分析后，可以转化为树形逻辑模型求解。

为什么这样用
递归与回溯的过程，本身就是穷举的过程。题目中要求我们列举每一个解的内容，解从哪来？解是基于穷举思想、对搜索树进行恰当地剪枝后得来的。

这里需要大家注意到另一种问法：不问解的内容，只问解的个数。这类问题往往不用 DFS 来解，而是用动态规划（我们后面会学）。这里，大家先记下这个辨析，对以后做题会有帮助。

怎么用
一个模型——树形逻辑模型；两个要点——递归式和递归边界。
树形逻辑模型的构建，关键在于找“坑位”，一个坑位就对应树中的一层，每一层的处理逻辑往往是一样的，这个逻辑就是递归式的内容。至于递归边界，要么在题目中约束得非常清楚、要么默认为“坑位”数量的边界。
用伪代码总结一下编码形式，大部分的题解都符合以下特征：

function xxx(入参) {
  前期的变量定义、缓存等准备工作 
  // 定义路径栈
  const path = []
  // 进入 dfs
  dfs(起点) 
  // 定义 dfs
  dfs(递归参数) {
    if(到达了递归边界) {
      结合题意处理边界逻辑，往往和 path 内容有关
      return   
    }
    // 注意这里也可能不是 for，视题意决定
    for(遍历坑位的可选值) {
      path.push(当前选中值)
      处理坑位本身的相关逻辑
      path.pop()
    }
  }
}

在面试中，如果你隐约觉得这道题用递归回溯来解可能有戏，却一时间没办法明确具体的解法，那么不妨尝试把这段伪代码记在脑子里。在面试时，先把框架写出来，然后结合题意去调整和填充伪代码的内容——很多时候，我们做题缺的不是知识储备，而是一个具体的切入点。