23 | 普通人也能吃透的动态规划思想专题（下）

在上一节，我们掌握了求解动态规划问题的通用套路。但正如我们前面所说，通用思路存在一定的局限性——它提供给大家的毕竟是一种方向性的引导，至于能不能实实在在地用自己的双手解决掉一道具体的题目，更多还是看同学们自己的“造化”。

所谓“造化”，其实并不神秘，它就是指我们自己对题目和知识点的思考深度和吸收程度。“造化”是否到位，并不取决于天赋，而是取决于每一位同学自身对题目的量的积累和对解题技术的总结。

作为对通用解题套路的补充，本节笔者基于自己接触过的海量动态规划真题，结合个人对面试命题倾向的观察和思考，提取了两个学习性价比极高的重点解题模型。
模型可以帮助我们迅速地识别并解决掉一类问题，通过对重点模型进行学习，大家可以在实战中做到举一反N，大大提升我们做题的效率和专业程度。

0-1背包模型

0-1背包问题是一个基本问题，基于这个基本问题，可以衍生出千姿百态的变种问题，这种题目就非常适合拿来构造解题模型。
0-1背包问题说的是这么回事儿：

有 n 件物品，物品体积用一个名为 w 的数组存起来，物品的价值用一个名为 value 的数组存起来；每件物品的体积用 w[i] 来表示，每件物品的价值用 value[i] 来表示。现在有一个容量为 c 的背包，问你如何选取物品放入背包，才能使得背包内的物品总价值最大？ 注意：每种物品都只有1件

思路分析

这道题如果全靠本能来做，相信不少同学会联想到“暴力枚举法”：暴力枚举每一件物品放或者不放进背包的情况。考虑到每一种物品都面临“放”和“不放”两种选择，因此 n 个物品就对应 2^n 种情况，进而会带来高达 O(2^n)的时间复杂度。这个时间复杂度是众多复杂度中相对来说比较恐怖的“指数量级”，我们是万万不能让这种东西出现在面试题解中的，因此果断放弃它。
现在我们放弃本能，回归理智，开始调度自己的智慧来做题：这道题最后问了“如何才能使背包内的物品总价值最大？”，我们前面讲过，遇到最值问题，一定要在可能的解题方案中给动态优化留下一席之地。事实上，背包系列问题，正是动态规划的标准对口问题。
下面我们基于通用解题思路来梳理一下这道题：

“倒推”法明确状态间关系

现在，假设背包已满，容量已经达到了 c。站在c这个容量终点往后退，考虑从中取出一样物品，那么可能被取出的物品就有 i 种可能性。我们现在尝试表达“取出一件”这个动作对应的变化，我用 f(i, c) 来表示前 i 件物品恰好装入容量为 c 的背包中所能获得的最大价值。现在假设我试图取出的物品是 i，那么只有两种可能：

1. 第 i 件物品在背包里
2. 第 i 件物品不在背包里

如果说本来这个背包中就没有 i 这个东西，那么尝试取之前和尝试取之后，背包中的价值总量是不会发生变化的。：

f(i, c) = f(i-1, c)

但如果背包中是有 i 的，那么取出这个动作就会带来价值量和体积量的减少：

f(i, c) - value[i] = f(i-1, c-w[i])

把这个减法关系稍微转化一下，变为加法关系：

f(i, c) = f(i-1, c-w[i]) + value[i]

可以看出，想要求出 f(i, c)，我们只要定位到正确的 f(i-1, c) 和 f(i-1, c-w[i]) + value[i] 的值，并且取出两者中较大的值就可以了。如此，我们便明确出了这道题的状态转移关系。现在我们需要思考的是如何把这种关系用代码的形式表达出来。
首先，基于上面的分析，我们抽取出自变量和因变量：自变量是物品的索引（假设为i）和当前背包内物品的总体积（假设为 v），因变量是总价值。我们仍然是用一个数组来记忆不同状态下的总价值，考虑到这道题中存在两个自变量，我们需要开辟的是一个二维数组。现在我利用二维数组来将上述的状态关系编码化：

dp[i][v] = Math.max(dp[i-1][v], dp[i-1][v-w[i]] + c[i])

以上便是这道题对应的状态转移方程。你会发现我前面真没忽悠你——只要能够利用“倒推”法明确出状态转移关系，我们根本没有必要去构造一个完整而复杂的树形思维模型，直接把状态转移方程往循环里塞就行。
为什么我这么笃定？别忘了，动态规划的关键特性就是“最优子结构”（对这个概念感到模糊的同学，赶紧回到上一节去复习一下）。这道题符合最优子结构的特征——dp[i]只和它之前的状态dp[i-1]有关。最优子结构允许我们推导一次就知晓全局，就是这么爽。
现在我们来瞅瞅这个状态转移方程怎么往循环里塞才合适。仍然是从变量入手：变量是 i 和 v，但本质上来说 v 其实也是随着 i 的变化而变化的，因此我们可以在外层遍历i、在内层遍历 v。明白了这一点，我们就可以编码如下：

for(let i=1;i<=n;i++) {
    for(let v=w[i]; v<=c;v++) {
      dp[i][v] = Math.max(dp[i-1][v], dp[i-1][v-w[i]]+value[i])
    }
}

现在，时间复杂度已经被我们优化到了 O(n)的水平，相当不错。但是空间复杂度其实还可以抢救一下。不过不着急，初学背包问题，我们先站在巩固思路的角度，重现一下这个二维数组的填充过程：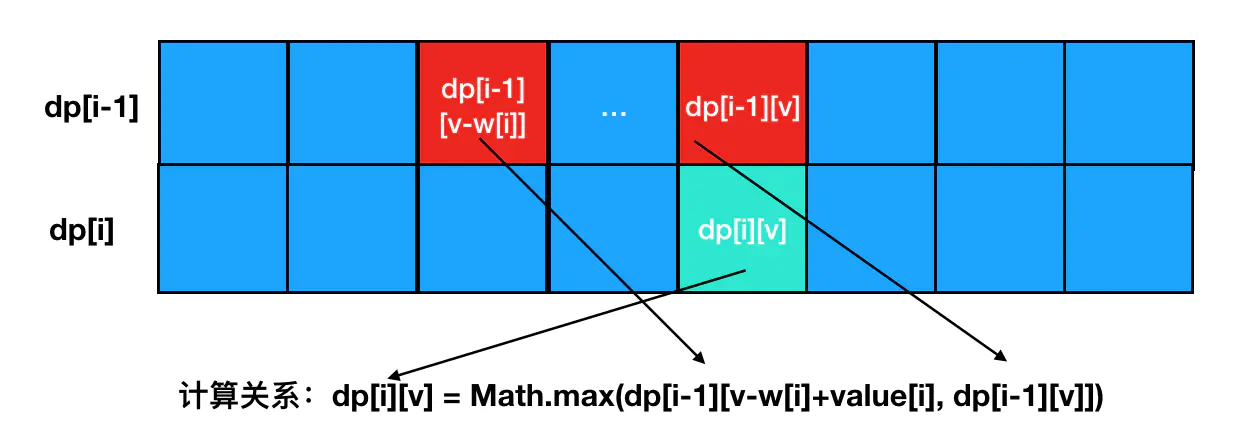

从图中我们可以看出，计算 dp[i][v] 的时候，其实只需要图中标红位置的数据就可以了（这与我们前面讲解过的最优子结构特性不谋而合），也就是说未标红的地方对于 dp[i][v] 的计算来说都属于冗余数据。实际上，对于第 i 行的计算来说，只有第 i-1 行的数据是有意义的，更早的数据它都不关心。也就是说我们其实根本不需要记录所有的数据，理论上只要保留当前行和上一行的数据就足够了。
一些教材或许会教你通过优化二位数组来节省空间上的开销，但这种手段在笔者看来无异于隔靴搔痒——要优化就优化到底，我们干脆把二维数组干掉，用一维数组来做。

插播小知识——滚动数组

这里要给大家介绍的是一种叫做“滚动数组”的编码思想——所谓“滚动数组”，顾名思义，就是让数组“滚动”起来：固定一块存储空间，滚动更新这块存储空间的内容，确保每个时刻空间内的数据都是当前真正会用到的最新数据，从而达到节约内存的效果，这种手段就叫做滚动数组。

用滚动数组来优化状态转移方程

我可以只定义一个一维数组，通过倒着遍历v的方法来实现数组的滚动更新：

for(let i=1;i<=n;i++) {
    for(let v=c;v>=w[i];v--) {
        dp[v] = Math.max(dp[v], d[v-w[i]]+value[i])
    }
}

这个方法到底骚在哪里？它为什么可以实现数组的滚动更新？接下来咱们就一起来瞅瞅这个数组是怎么“滚”的：
拿第 i-1行和第i行来举例，首先我肯定是刷刷刷地用第 i-1 行的数据把一维数组给填满了（这里我保留了对关键计算线索的高亮）：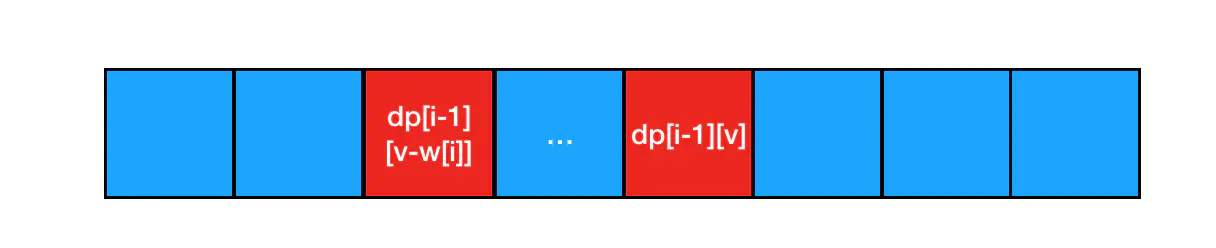
接下来我尝试用第 i 行的数据更新它。当数据更新走到 dp[i][v] 这里的时候，dp[i-1][v] 和 dp[i-1][v-w[i]] 都是存在的状态（分别对应一维数组中现在的 dp[v]和dp[v-w[i]]的值，完全可以满足我们的计算需要：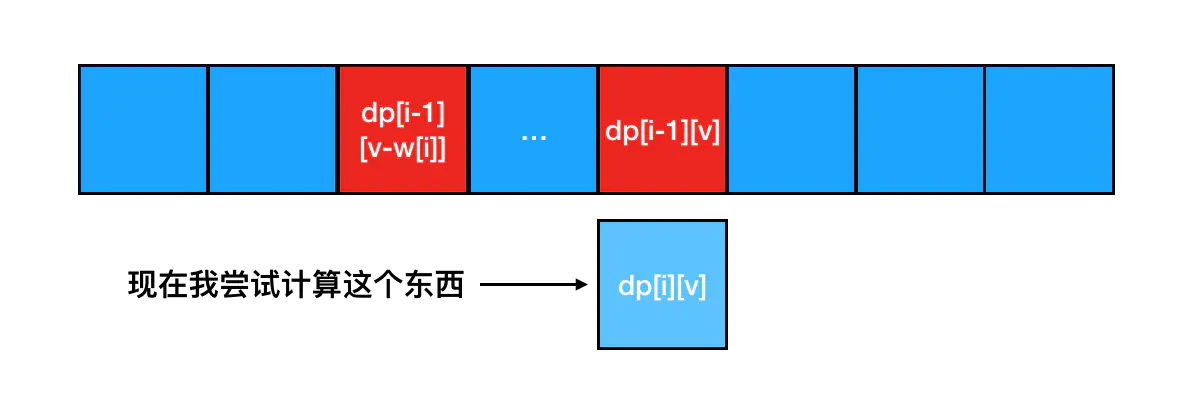

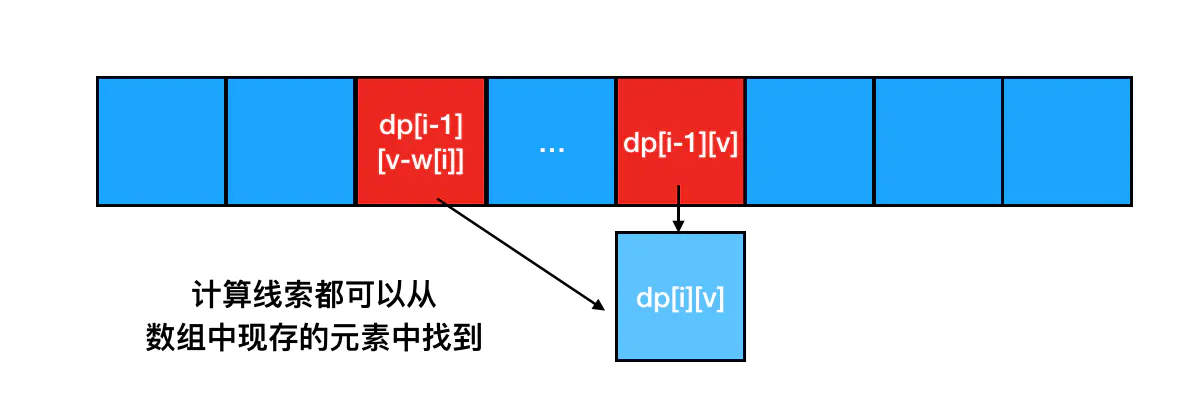当我们计算出 dp[i][v] 的值以后，dp[i-1][v-w[i]]可能还会在以后的计算中用到，但dp[i-1][v]其实已经完全用不到了（这个点对初学的同学来说可能会有点绕，不要慌，你品，你细品。注意这里dp[i][v]已经求解出来了，对于 i 这个索引来说只需要求解 dp[i][v-1]到dp[i][w[i]]之间的值，仔细想想，求解这些值是不是完全用不到dp[i-1][v]？）。
此时我们刚好用 dp[i][v] 去更新了 dp[v] 的值，把用不到的数据给及时地替换掉了，岂不美滋滋？
基于上面的分析，我们可以写出背包问题的完整求解代码：

// 入参是物品的个数和背包的容量上限，以及物品的重量和价值数组
function knapsack(n, c, w, value) {
    // dp是动态规划的状态保存数组
    const dp = (new Array(c+1)).fill(0)  
    // res 用来记录所有组合方案中的最大值
    let res = -Infinity
    for(let i=1;i<=n;i++) {
        for(let v=c;v>=w[i];v--) {
            // 写出状态转移方程
            dp[v] = Math.max(dp[v], dp[v-w[i]] + value[i])
            // 即时更新最大值
            if(dp[v] > res) {
                res = dp[v]
            }
        }
    }
    return res
}

最长上升子序列模型

该模型对口的其实是动态规划中一类非常经典的问题——“序列型动态规划”。在形态各异的序列型动态规划问题中，“最长上升子序列”问题可以说是相当热门的，其解法也是比较具有代表性的。接下来我们就以这个问题为抓手，提取其对应的的解题模型。

题目描述：给定一个无序的整数数组，找到其中最长上升子序列的长度。 示例: 输入: [10,9,2,5,3,7,101,18]

输出: 4
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

说明:

可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。 你算法的时间复杂度应该为 O(n^2) 。
进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?

思路分析

在做一道题之前，首先要知道题目到底在说啥，这里可能会对初学者构成理解障碍的关键字有两个：“子序列”和“上升”。
啥是“子序列”？它指的是在原有序列的基础上，删除0个或者多个数，其他数的顺序保持不变得到的结果。拿示例的这个序列来说：

[10,9,2,5,3,7,101,18]

随便拿掉0个数或多个数：比如说我去掉第一个数字10，去掉最后一个数18，但是不打乱这个序列的顺序，那么我得到的新的序列就是该序列的一个子序列：

[9,2,5,3,7,101]

啥是“上升”？这个就比较好理解了，它指的是排在后面的元素总是要大于排在前面的元素。
在上一节，我们曾经学习过一种“通用解题思路”。通用解题思路的核心，是利用递归思想，以“倒推”为抓手，快速地明确状态与状态间的关系。当我们面对一道题目，无从下手的时候，这个思维工具往往能够帮到我们很大的忙。
然而，事事无绝对，学习动态规划并不是掌握一个套路就可以高枕无忧的“一锤子买卖”。对于最长上升子序列问题来说，通用解题思路所描述的这种“自顶向下”的思维方式，并不好使。
事实上，做这道题，大家要把握住一个关键的特征，那就是“序列”。
这道题比较直白，直接把“序列”二字写在了题干里。后面我们会做到一些更有趣（同时也更拧巴）的题目，这些题目不会直接跟你说它是序列类型题目，但是通过对题干进行分析，你会发现它实际上仍然会涉及到对一个序列的遍历，并且序列中的每一个元素都能够对应到一个有利于求解出最终结果的状态值，这类题目也符合“序列”的特征。
对于序列类题目，我们并没有一套固定的解题模型可以直接套，一般来说只能见招拆招，针对不同的题型分支套不同的解法（所以确实需要大家有一定程度的题量上的积累）。解法虽有不同，背后的思想却是一而贯之的，那就是关注到序列中元素的索引，尝试寻找不同索引对应的元素之间的关系、并以索引为线索去构造一维或二维的状态数组。
拿“最长上升子序列”这个问题分支来说，这里我们关注到的就是“以序列中第 **i** 个元素为结尾的前**i**个元素的状态”。
我们用f(i)来表示前i个元素中最长上升子序列的长度。若想基于 f(i) 求解出 f(i+1)，我们需要关注到的是第 i+1 个元素和前 i 个元素范围内的最长上升子序列的关系，它们之间的关系有两种可能：

1. 若第i+1个元素比前i个元素中某一个元素要大，此时我们就可以在这个元素所在的上升子序列的末尾追加第i+1个元素（延长原有的子序列），得到一个新的上升子序列。
2. 若第i+1个元素并不比前i个元素中所涵盖的最长上升子序列中的某一个元素大，则维持原状，子序列不延长。

这个过程形容起来可能比较抽象，下面我们用一个示例来理解它。
拿我们题目示例中的数组[10,9,2,5,3,7,101,18]来举例。在算法的初始态，我们还没有进行任何的遍历和计算，此时对于每一个索引位来说，它都只与一个长度为1的子序列有关——那就是只有它自己存在的子序列。因此每一个索引位对应的状态初始值都是1：
同时对于索引位为0的元素来说，由于以它为结尾的子序列有且仅有 [10] 这一个，因此它的状态值时一开始就明确的，那就是1：

f(0) = 1

下面基于 f(0) 对 f(1) 求解，比较两个索引位上元素的大小：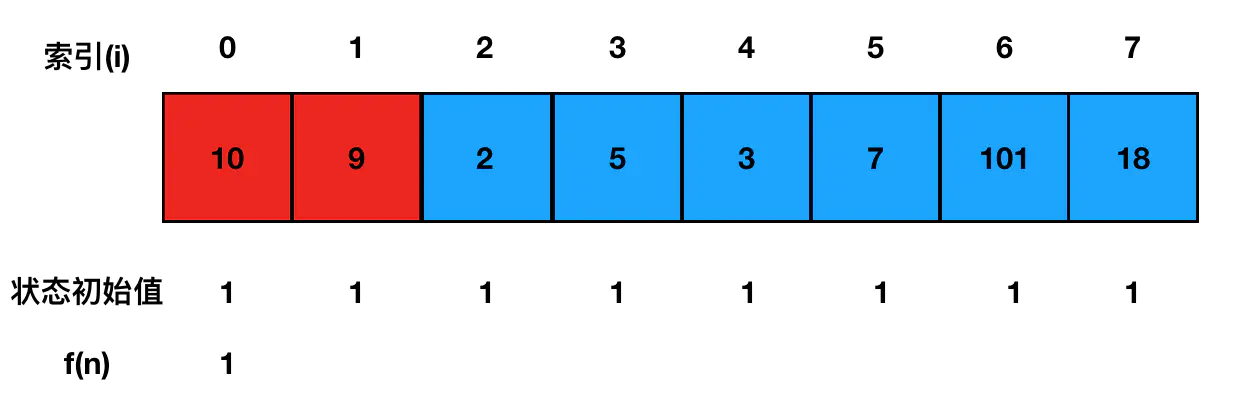
发现9比10小，没办法延长原有的子序列，因此啥也不干。继续往下遍历，遇到了2，发现2比前两个数都小，仍然没法延长任何一个子序列，继续啥也不干。
再往下遍历，遇到了5，对比5和前面三个元素，发现它比2大，可以延长2所在的那个最长上升子序列，延长后，以 5 为结尾的最长上升子序列的长度就得到了更新：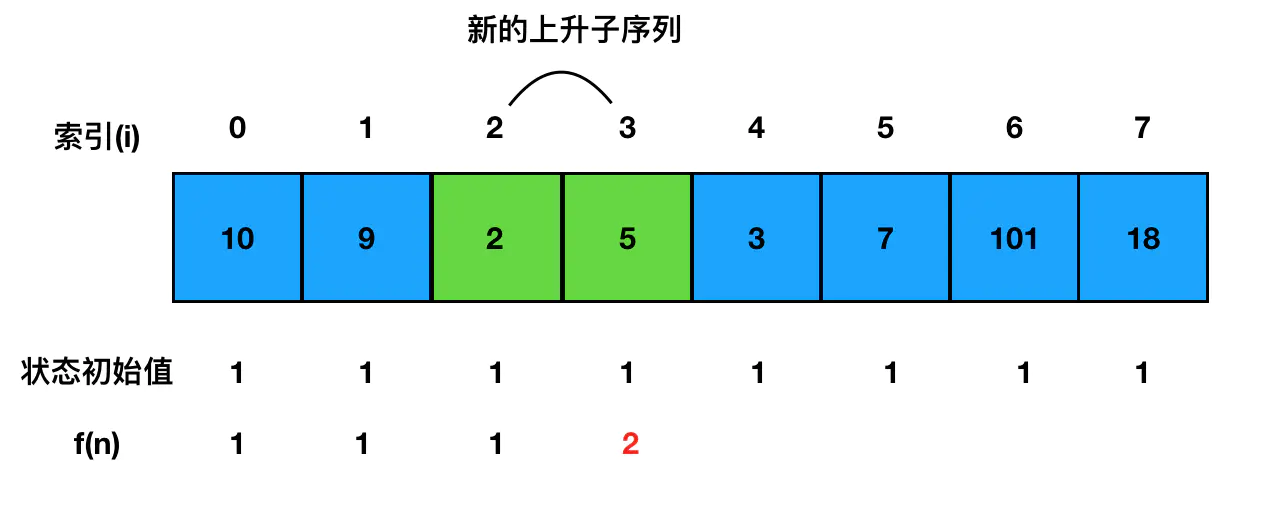

重复上面这个“遍历新元素+回头看”的逻辑，直到整个数组被完全遍历，我们就能拿到以每一个索引位元素为结尾的最长上升子序列的长度值。从这些长度值中筛选出最大值，我们也就得到了问题的解。
我们基于这个思路进行编码：

编码实现

/**
 * @param {number[]} nums
 * @return {number}
 */
// 入参是一个数字序列
const lengthOfLIS = function(nums) {
  // 缓存序列的长度
  const len = nums.length  
  // 处理边界条件
  if(!len) {
      return 0
  }
  // 初始化数组里面每一个索引位的状态值
  const dp = (new Array(len)).fill(1)
  // 初始化最大上升子序列的长度为1
  let maxLen = 1 
  // 从第2个元素开始，遍历整个数组
  for(let i=1;i<len;i++) {
      // 每遍历一个新元素，都要“回头看”，看看能不能延长原有的上升子序列
      for(let j=0;j<i;j++) {  
          // 若遇到了一个比当前元素小的值，则意味着遇到了一个可以延长的上升子序列，故更新当前元素索引位对应的状态
          if(nums[j]<nums[i]) {
              dp[i] = Math.max(dp[i], dp[j] + 1)  
          }
      }
      // 及时更新上升子序列长度的最大值
      if(dp[i] > maxLen) {
          maxLen = dp[i]
      }
  }
  // 遍历完毕，最后到手的就是最大上升子序列的长度
  return maxLen
};

问题复盘

对于这道题，其实也可以用最原始的办法来枚举每种情况：对于每个元素，考虑“取”和“不取”两种选择，得到对应的序列，进而判断这个序列是否是一个上升序列。若得到的是上升序列，则计算并更新最大长度；若不是，则啥也不干。
基于这个枚举的思路，我们不难想出递归的解法，然后再结合记忆化搜索，这道题似乎也能用“自顶向下”的求解思路做出来。
这里不推荐大家延续“自顶向下”的思维方式，原因有两个：

1. 这类题目有稳定的解题模型，可以帮助我们更好更快地解决问题，大可不必舍近求远
2. 帮助大家完成从递归思想向动态规划思想的过渡，避免思维定式。

在初学动态规划时，为了避免架空式地理解一个全新思想所带来的不适，我们需要借助已经学过的递归思想作为“垫脚石”来辅助我们的理解，从而跨过最难的第一道门。在基于递归思想的解题模板的帮助下，相信大家都对“倒推”法明确状态转移关系这个套路有了深刻的理解，同时也难免会有这样的困惑——难道动态规划就是记忆化搜索的迭代实现吗？这跟脱裤子放屁有什么区别？
如果你曾经有过这样的困惑，相信本节的学习已经为你解开心结——动态规划并不是任何一种其他算法思想的“替代品”，它有着自己独特的思路和作用。我们之所以在前面的几道题中会用到递归，是因为递归能够帮助我们又好又快地定位状态转移关系——递归是手段，而不是目的。在最大上升子序列这个问题中，我们可以看出，状态转移关系虽然总是涉及到对前后两个状态的分析，却并不总是依赖递归。
在后续的“大厂真题训练”环节中，大家会见识到更多千姿百态的动态规划题目。其中有一部分，可以完全借助我们这两节所讨论过的经验来解决；还有一部分，需要你“见招拆招”。不过不要怕，只要你把握住了“重叠子问题”和“最优子结构”两个关键特征，把握住了动态规划的核心解题逻辑，那么再新的题目也只不过是对你已经掌握的动态规划之“道”的验证，是对解题之“术”的拓展。