本节内容不要求所有同学掌握——如果你在阅读的过程中，觉得理解起来非常吃力，笔者建议你暂时跳过这一节，优先完成全盘的知识点扫盲后再回来看。
为什么这样说？这里面有两个原因：
- 根据笔者长期奋战算法面试一线的经验，能用堆结构解决的问题，基本上也都能用普通排序来解决。
- 即便是后端工程师或者算法工程师，能够在面试现场手写堆结构的人也寥寥无几。这倒不是因为他们不够专业，而是因为他们基本都非常熟悉一门叫做
JAVA的语言——JAVA大法好，它在底层封装了一个叫做priorty_queue的数据结构，这个数据结构把堆的构建、插入、删除等操作全部做掉了。所以说这帮人非常喜欢做堆/优先队列相关的题目，调几个API就完事儿了。
那么为什么还要讲堆结构，堆结构在我们整个知识体系里的定位应该怎么去把握，这里有两件事情希望大家能明白：
- 几乎每一本正经的计算机专业数据结构教材，都会介绍堆结构。小册本身虽然是面向面试的，但笔者更希望能借这个机会，帮助一部分没有机会接受科班教育的前端同行补齐自身的知识短板。
笔者个人在素材调研期间经历过的
N次涉及算法的前端面试中，有1次真的考到了需要用堆结构解决的问题（这道题在下面的讲解中也会出现）。当时笔者还不知道堆的玩法，直接用JS的排序API做出来了。事后和面试官聊天的时候，突然被他要求用堆结构再做一遍。最后虽然在没写出来的情况下拿到了offer，但事后想起来，还是非常后怕——没有人能预知自己下一次遇到的面试官到底是什么脾气，我们只能尽自己所能地去做万全的准备。前置知识：完全二叉树
完全二叉树是指同时满足下面两个条件的二叉树：
从第一层到倒数第二层，每一层都是满的，也就是说每一层的结点数都达到了当前层所能达到的最大值
- 最后一层的结点是从左到右连续排列的，不存在跳跃排列的情况（也就是说这一层的所有结点都集中排列在最左边）。
完全二叉树可以是这样的：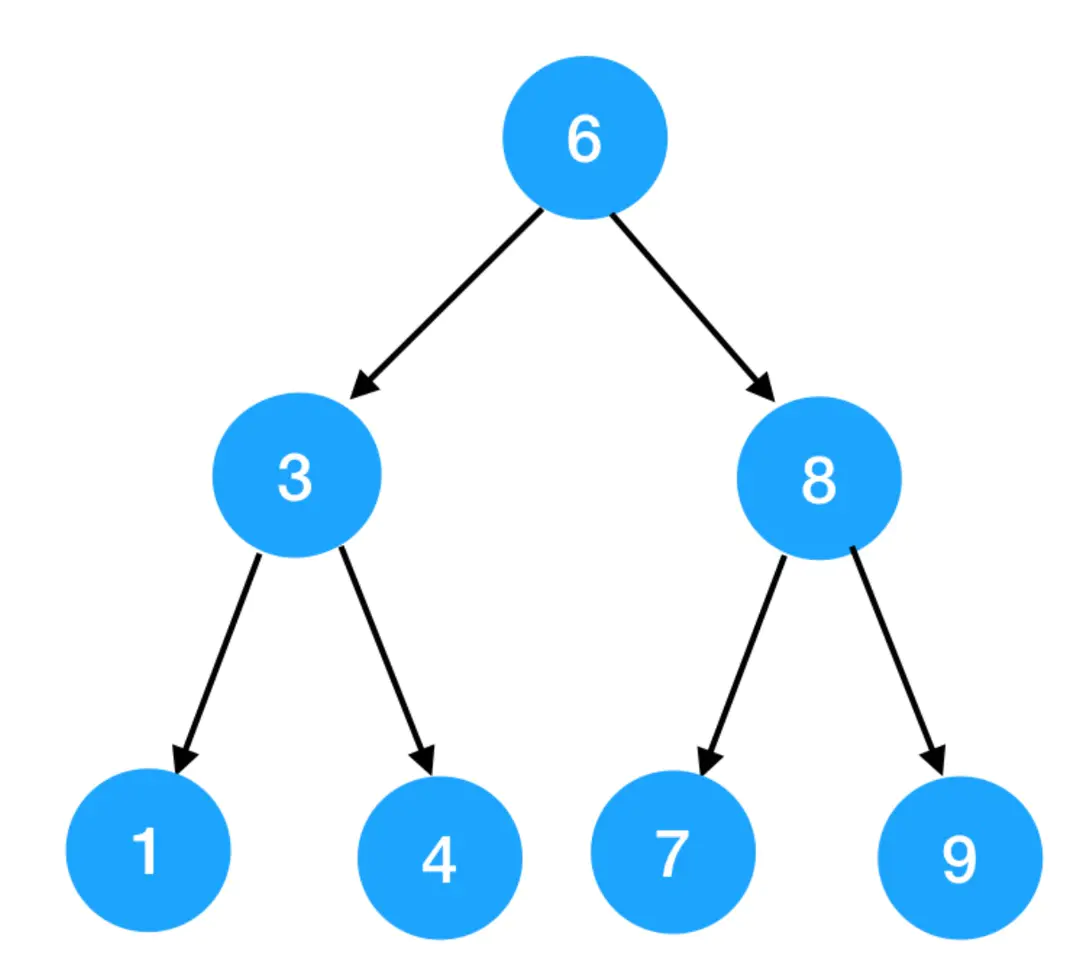
也可以是这样的：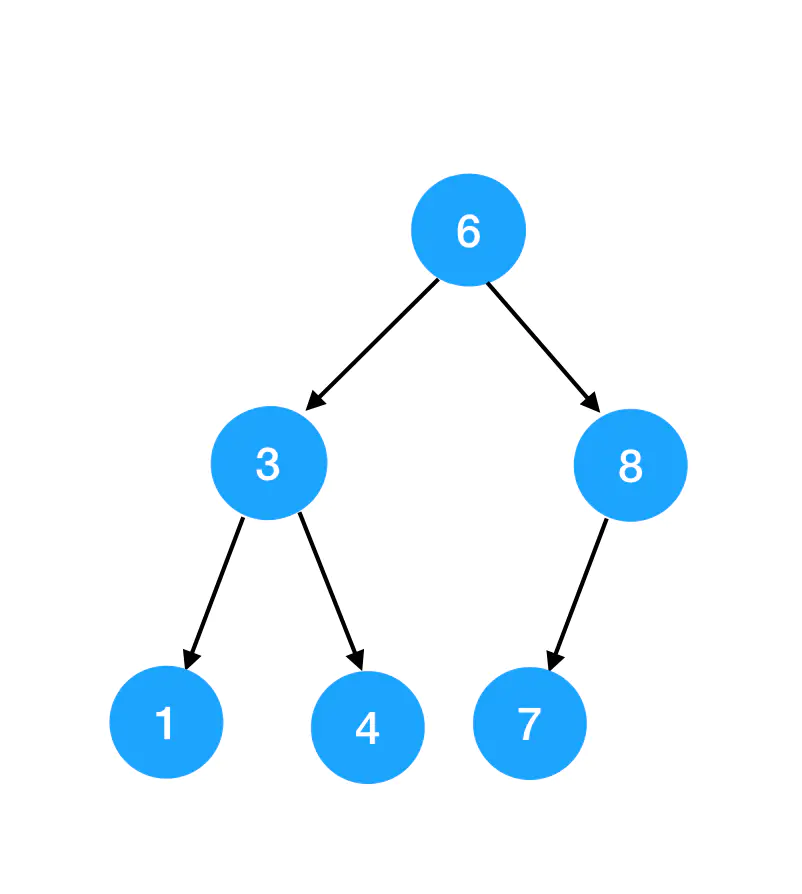
但不能是这样的：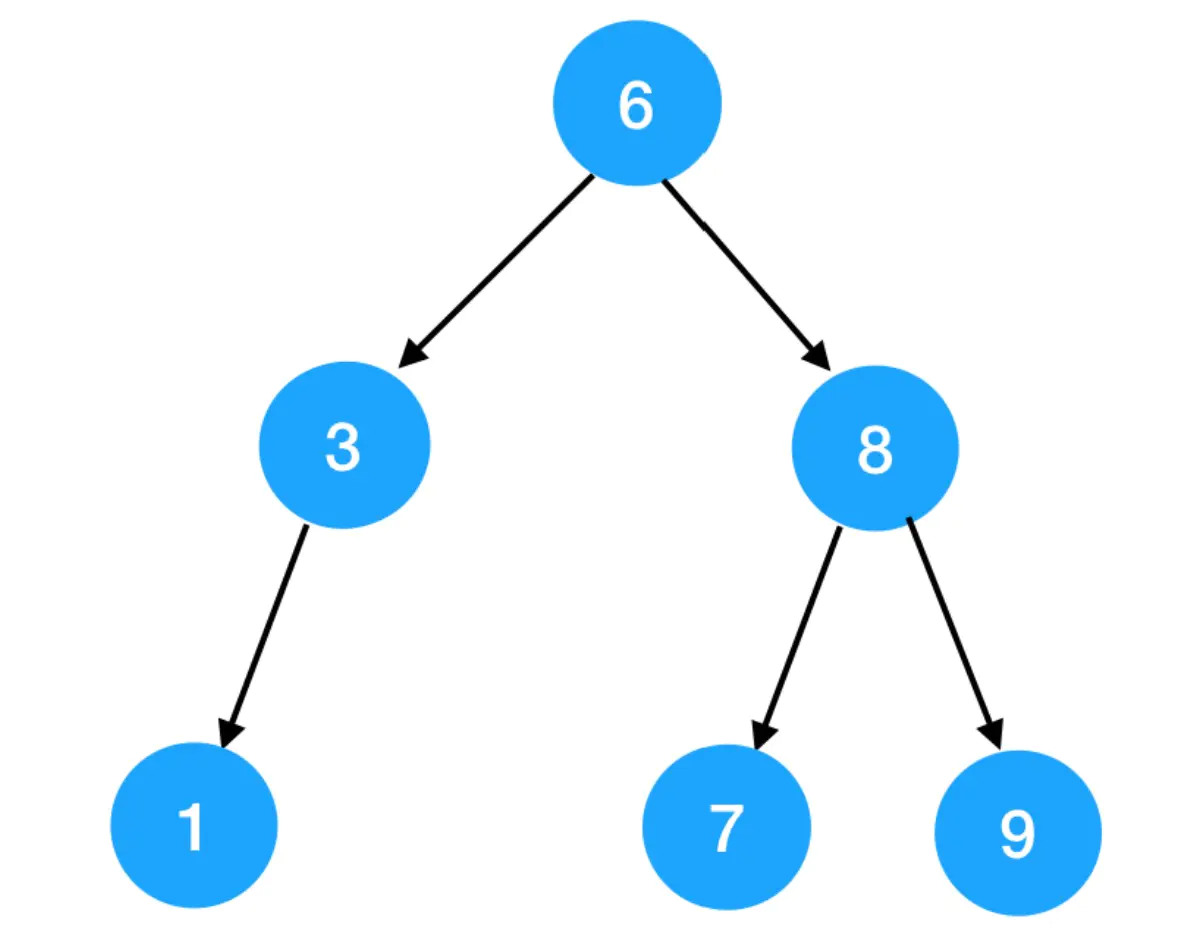
更不能是这样的：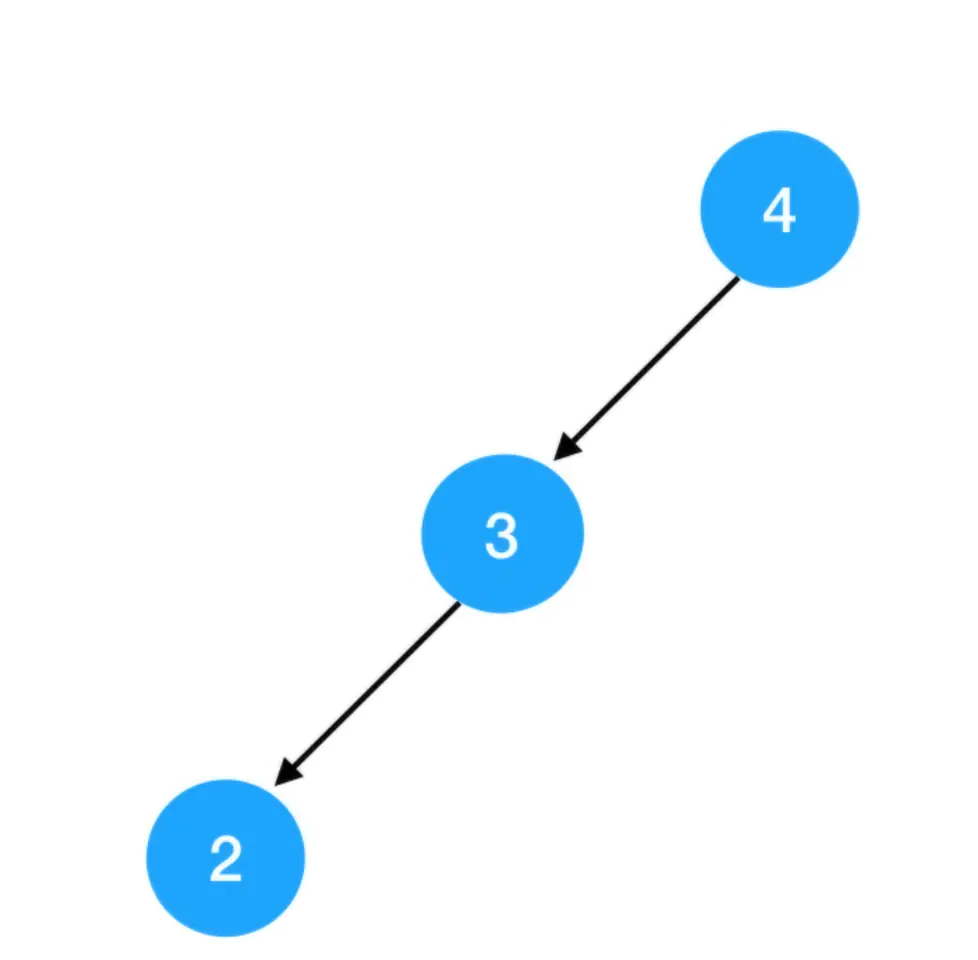
注意，完全二叉树中有着这样的索引规律：假如我们从左到右、从上到下依次对完全二叉树中的结点从0开始进行编码：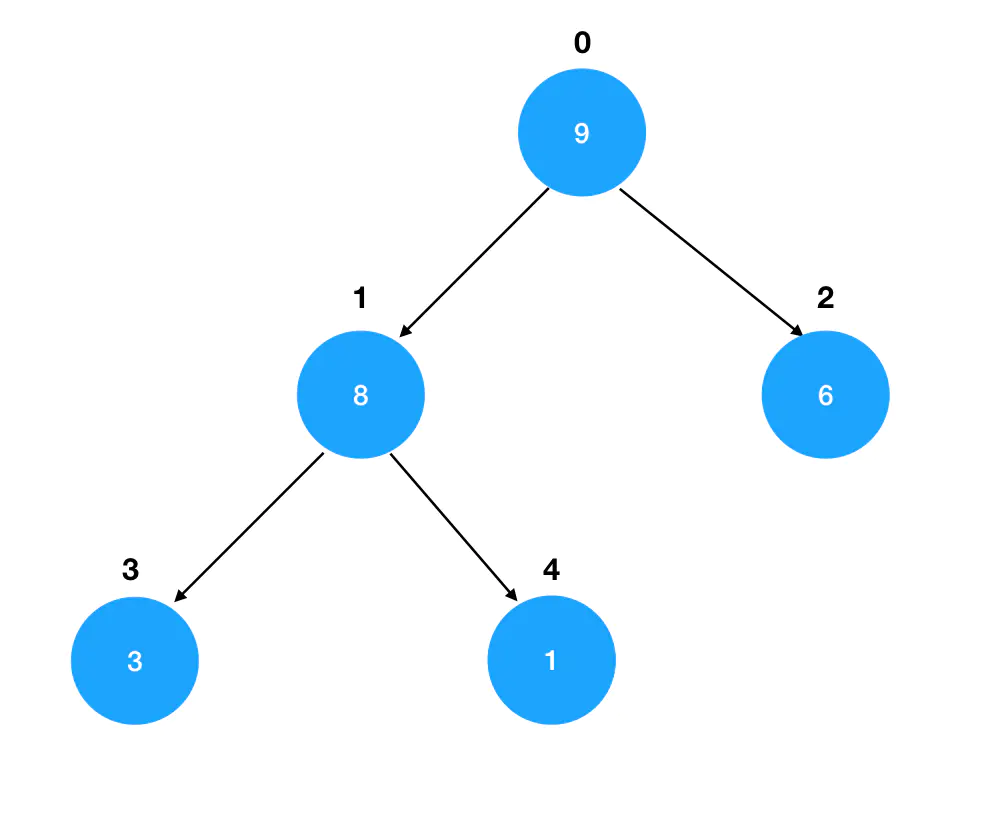
那么对于索引为 n 的结点来说：
如果对一棵完全二叉树来说，它每个结点的结点值都不小于其左右孩子的结点值，这样的完全二叉树就叫做“大顶堆”：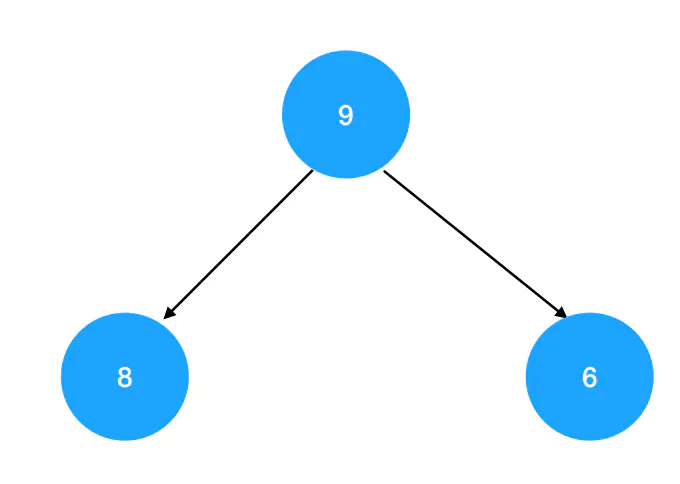
若树中每个结点值都不大于其左右孩子的结点值，这样的完全二叉树就叫做“小顶堆”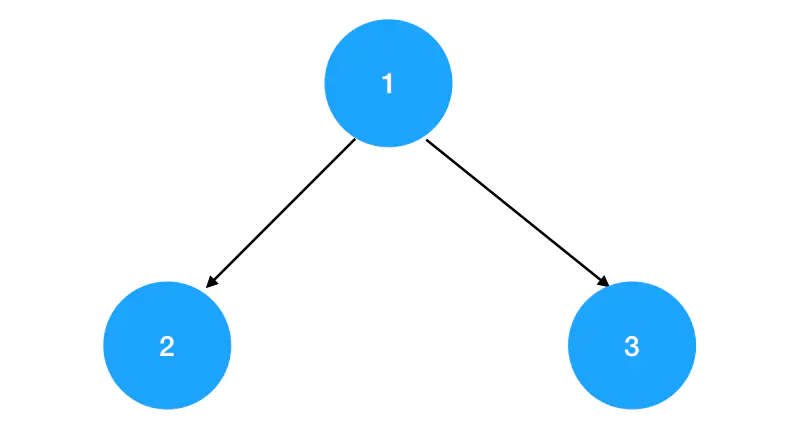
堆的基本操作：以大顶堆为例
大顶堆和小顶堆除了约束条件中的大小关系规则完全相反以外，其它方面都保持高度一致。现在我们以大顶堆为例，一起来看看堆结构有哪些玩法。
这里我给出一个现成的大顶堆：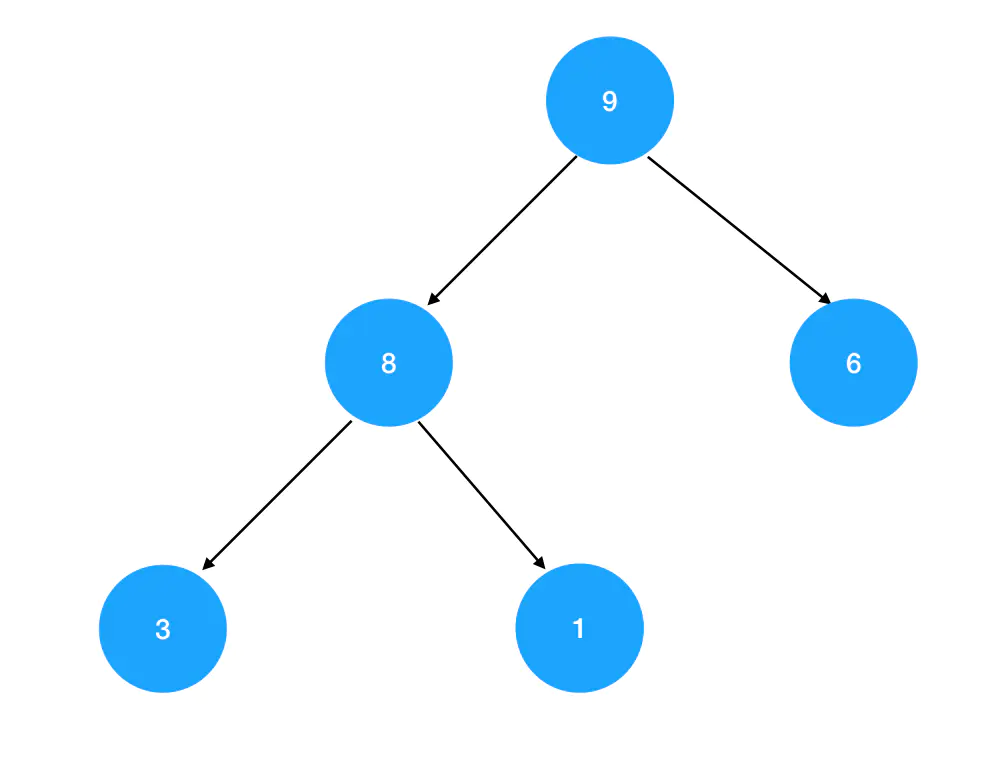
很多时候，为了考察你对完全二叉树索引规律的掌握情况，题目中与堆结构同时出现的，还有它的层序遍历序列：
[9, 8, 6, 3, 1]
（现在赶快回去复习一下完全二叉树的索引规律，我们马上写代码要用到了）
我们需要关注的动作有两个：
- 如何取出堆顶元素（删除操作）
- 往堆里追加一个元素（插入操作）
至于堆的初始化，也只不过是从空堆开始，重复执行动作2而已。因此，上面这两个动作就是堆操作的核心。
取出堆顶元素
取出元素本身并不难，难的是如何在删除元素的同时，保持住队的“大顶”结构特性。为了做到这点，我们需要执行以下操作：
- 用堆里的最后一个元素（对应图中的数字1）替换掉堆顶元素。
- 对比新的堆顶元素（1）与其左右孩子的值，如果其中一个孩子大于堆顶元素，则交换两者的位置：
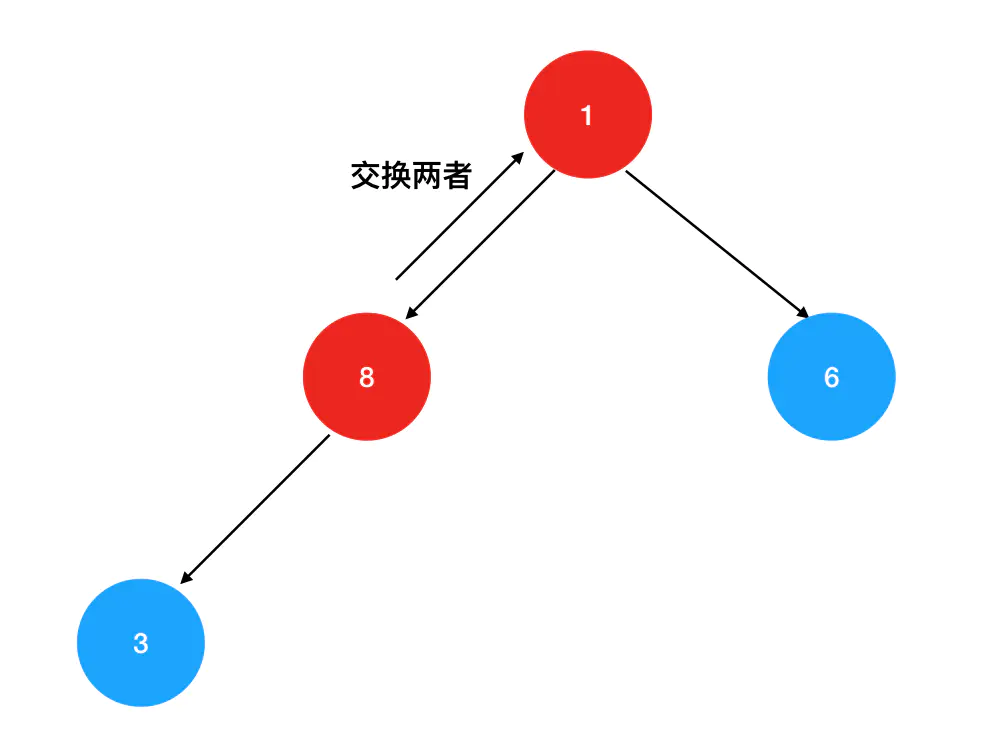交换后，继续向下对比1与当前左右孩子的值，如果其中一个大于1，则交换两者的位置：
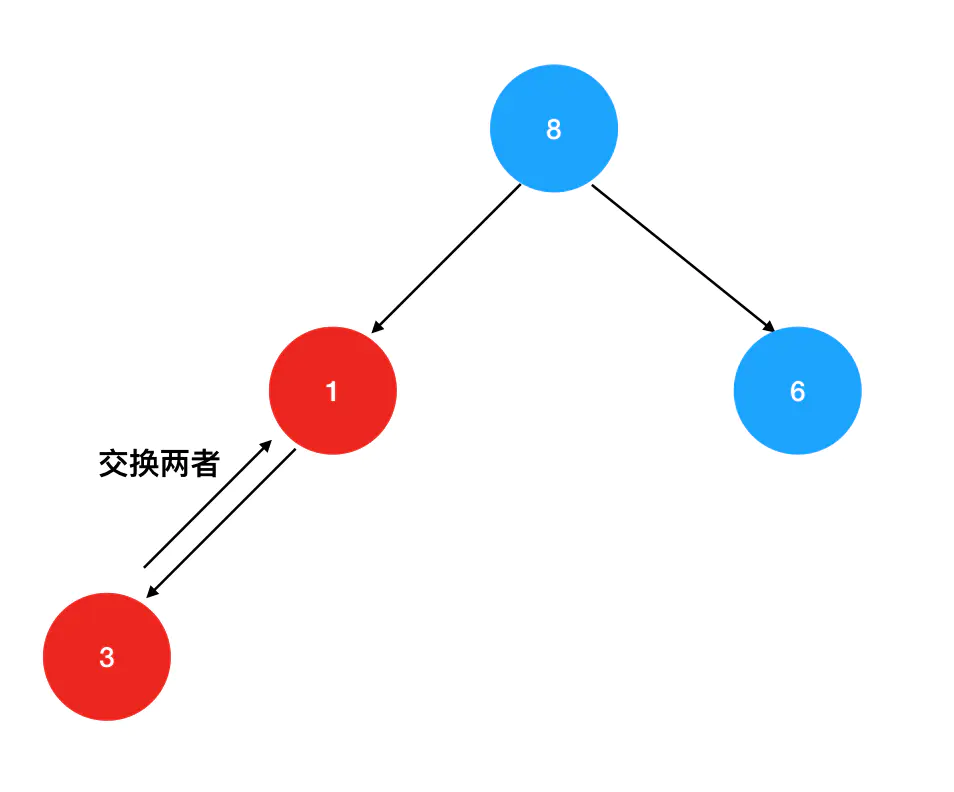重复这个向下对比+交换的过程，直到无法继续交换为止，我们就得到了一个符合“大顶”原则的新的堆结构：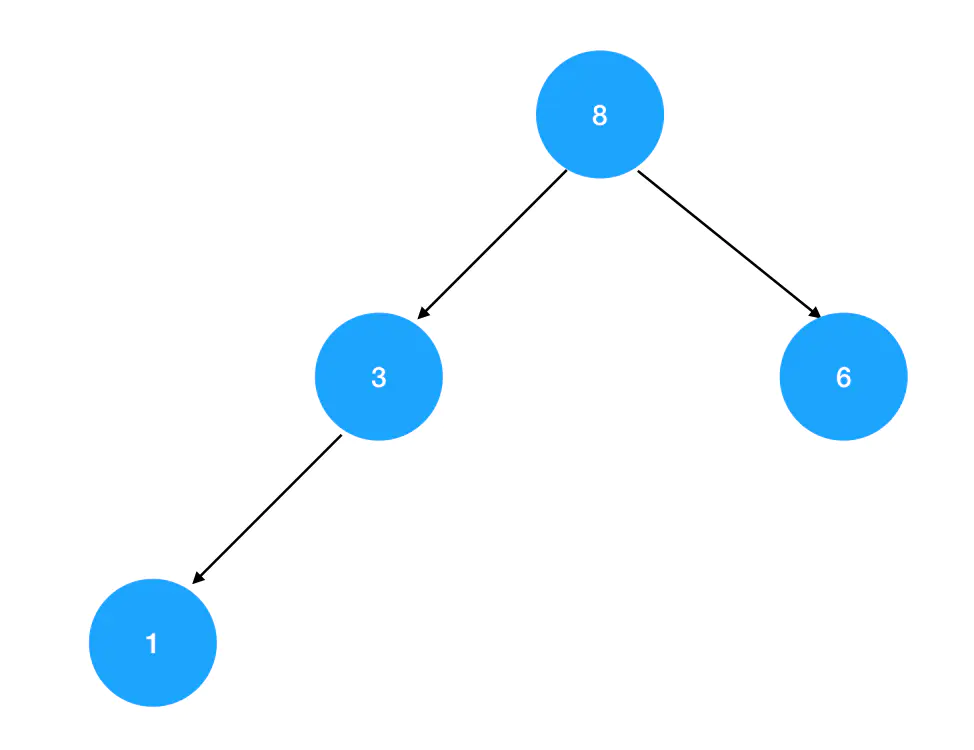
上述这个反复向下对比+交换的过程，用编码实现如下（仔细看注释）：
// 入参是堆元素在数组里的索引范围，low表示下界，high表示上界function downHeap(low, high) {// 初始化 i 为当前结点，j 为当前结点的左孩子let i=low,j=i*2+1// 当 j 不超过上界时，重复向下对比+交换的操作while(j <= high) {// 如果右孩子比左孩子更大，则用右孩子和根结点比较if(j+1 <= high && heap[j+1] > heap[j]) {j = j+1}// 若当前结点比孩子结点小，则交换两者的位置，把较大的结点“拱上去”if(heap[i] < heap[j]) {// 交换位置const temp = heap[j]heap[j] = heap[i]heap[i] = temp// i 更新为被交换的孩子结点的索引i=j// j 更新为孩子结点的左孩子的索引j=j*2+1} else {break}}}
往堆里追加一个元素
当添加一个新元素进堆的时候，我们同样需要考虑堆结构的排序原则：
- 新来的数据首先要追加到当前堆里最后一个元素的后面。比如我现在要新增一个10，它就应该排在最后一层的最后一个位置：
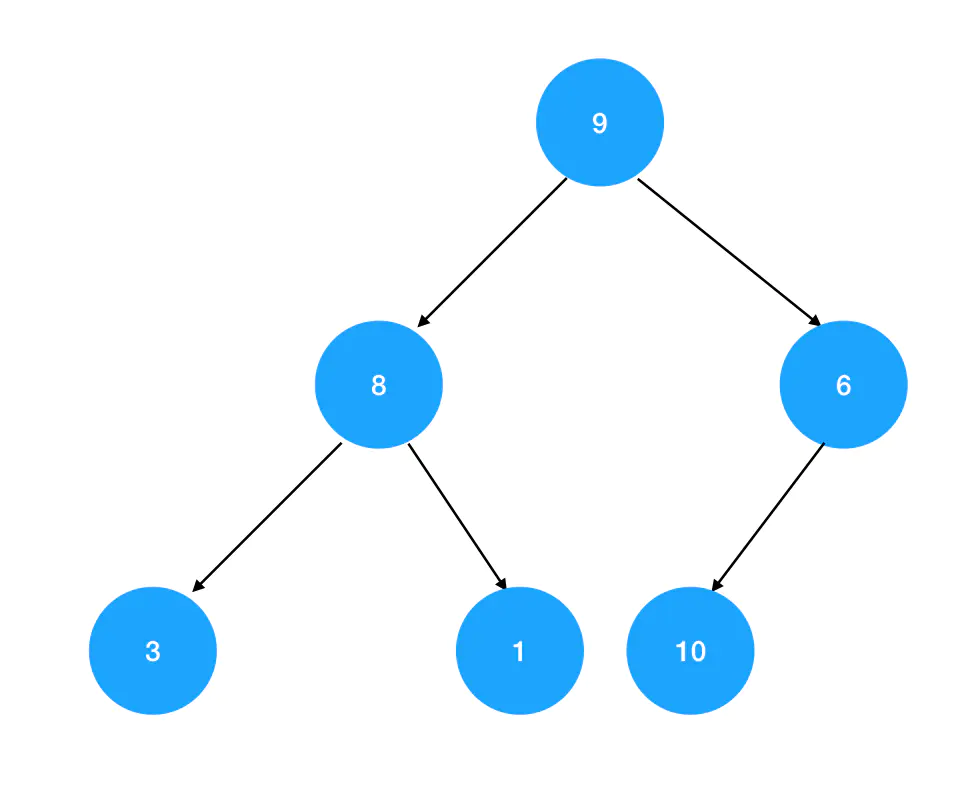2. 不断进行向上对比+交换的操作：如果发现10比父结点的结点值要大，那么就和父结点的元素相互交换，再接着往上进行比较，直到无法再继续交换为止。首先被比下去的是值为6的直接父结点：
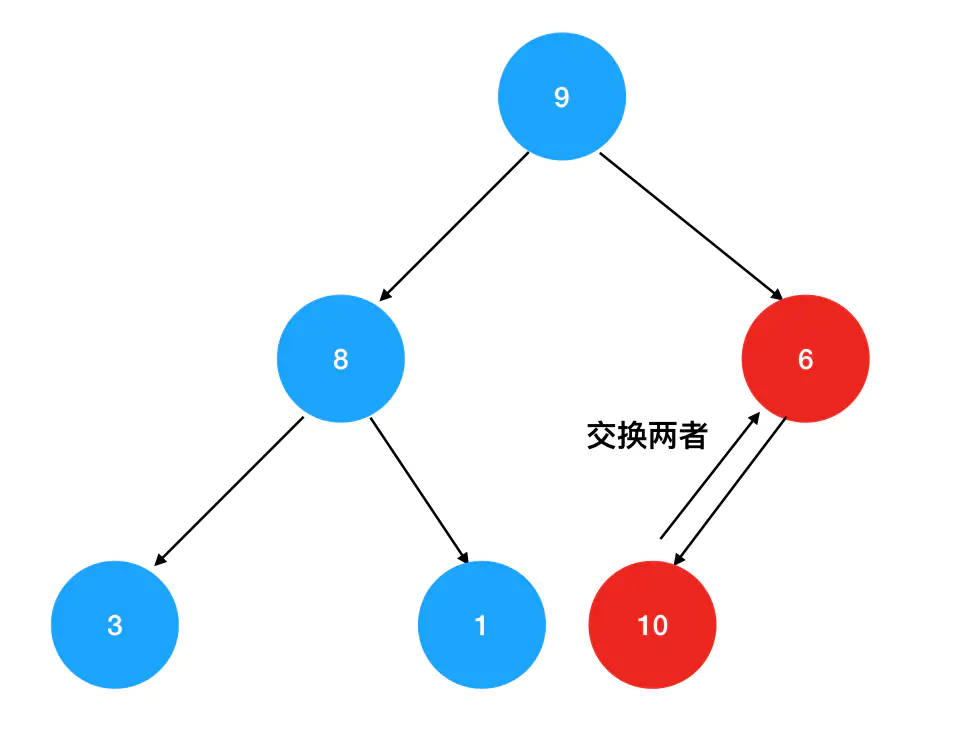接着继续往上找，发现10比根结点9还要大，于是继续进行交换：
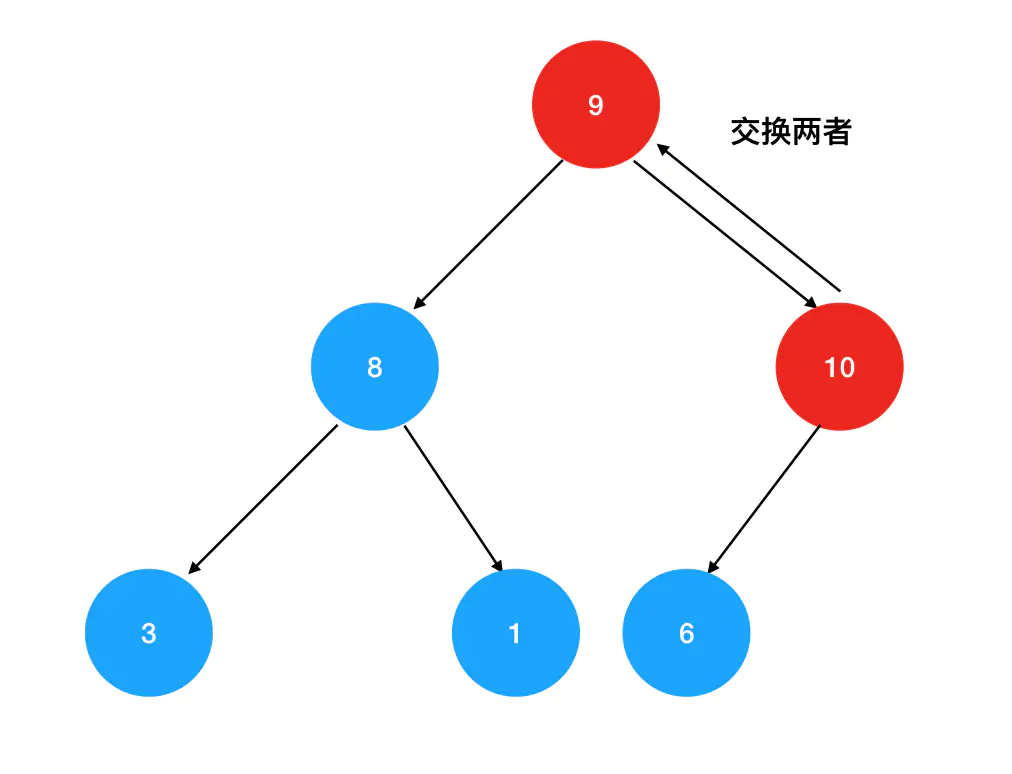根结点被换掉后，再也无法向上比较了。此时，我们已经得到了一个追加过数字10的新的堆结构：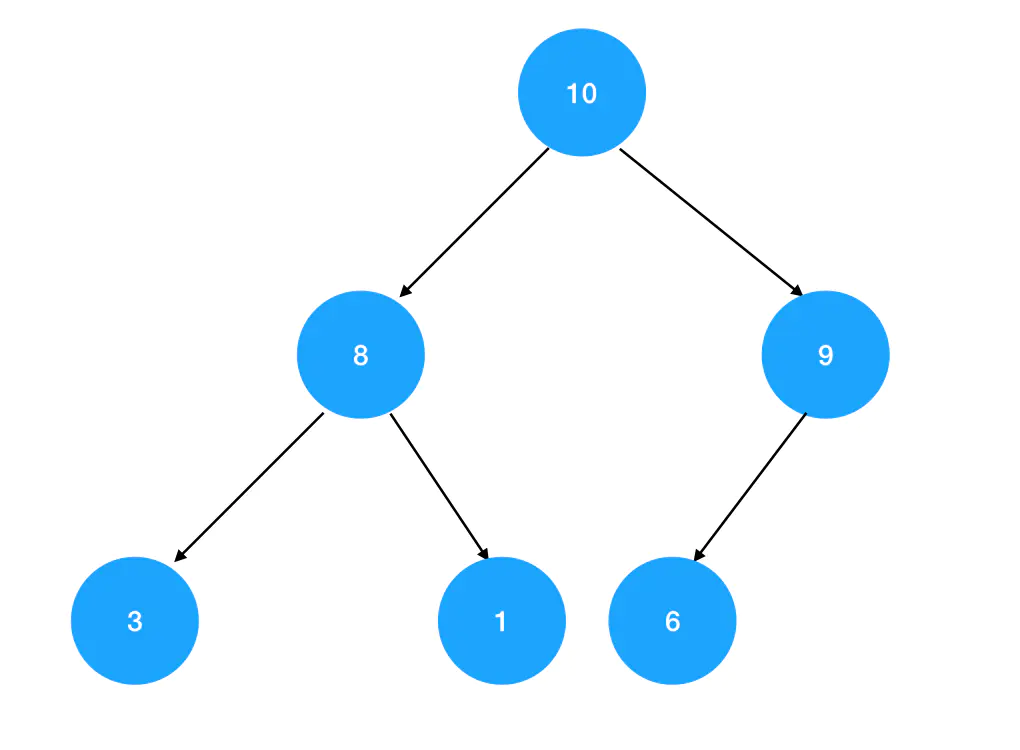
上述这个反复向上对比+交换的过程，用编码实现如下（仔细看注释）：
// 入参是堆元素在数组里的索引范围，low表示下界，high表示上界function upHeap(low, high) {// 初始化 i（当前结点索引）为上界let i = high// 初始化 j 为 i 的父结点let j = Math.floor((i-1)/2)// 当 j 不逾越下界时，重复向上对比+交换的过程while(j>=low) {// 若当前结点比父结点大if(heap[j]<heap[i]) {// 交换当前结点与父结点，保持父结点是较大的一个const temp = heap[j]heap[j] = heap[i]heap[i] = temp// i更新为被交换父结点的位置i=j// j更新为父结点的父结点j=Math.floor((i-1)/2)} else {break}}}
上面这两个过程，需要大家反复理解、深刻记忆。尤其是要记住这几个关键字：“删除”就是“向下比较+交换”，而“添加”则是“向上比较+交换”。
这里写给大家的两段代码，在实战中具备一定的通用性。希望大家能够充分熟悉，在理解的基础上记忆。下次如果真的用到，争取能够默写。
堆结构在排序中的应用——优先队列
在认识优先队列之前，我们先来看一道题：
题目描述：在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。 示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:
你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。
思路分析
这道题的诉求非常直接——要求你对给定数组进行排序。关于排序，我们在下一节会展开讲解N种排序算法的实现方式，包括快速排序、归并排序、选择排序等等。这些排序有一个共同的特点——在排序的过程中，你很难去明确元素之间的大小关系，只有在排序彻底完成后，你才能找出第 k 大的元素是哪个。
对整个数组进行排序、然后按顺序返回索引为k-1的元素，这正是笔者在面试场上写出的第一个解法：
/*** @param {number[]} nums* @param {number} k* @return {number}*/const findKthLargest = function(nums, k) {// 将数组逆序const sorted = nums.sort((a,b)=> {return b-a})// 取第k大的元素return sorted[k-1]};;
是的，你没有看错，我甚至没有手动实现任何一个排序算法，而是直接调了 JS 的sort 方法。
大家不要笑，这个sort方法真的可以救命。如果你理解不了本节接下来要讲的基于堆结构的解法，又没信心记住后面两节涉及的各种各样的花式排序算法。那么你一定要紧紧抓住这个sort API。面试的时候，万一被问到“你为什么不会写xx排序算法”，这时候用一句“我用sort方法比较多，不喜欢自己造轮子”糊弄过去，还是有一定成功率的。
好了，学渣小剧场结束。我们继续来看这个题：有没有一种排序方法能够在不对所有元素进行排序的情况下，帮我们提前定位到第 k 大的元素是哪个呢？当然有——构建一个堆结构就能解决问题！
对于这道题来说，要想求出第 k 大的元素，我们可以维护一个大小为 k 的小顶堆。这个堆的初始化过程可以通过遍历并插入数组的前 k 个元素来实现。当堆被填满后，再尝试用数组的第 k+1 到末尾的这部分元素来更新这个小顶堆，更新过程中遵循以下原则：
- 若遍历到的数字比小顶堆的堆顶元素值大，则用该数字替换掉小顶堆的堆顶元素值
- 若遍历到的数字比小顶堆的堆顶元素值小，则忽略这个数字
仔细想想，为什么要这样做？假设数组中元素的总个数是 n，那么：
- 维护大小为
k的小顶堆的目的，是为了确保堆中除了堆顶元素之外的k-1个元素值都大于堆顶元素。 - 当我们用数组的
[0, k-1]区间里的 数字初始化完成这个堆时，堆顶元素值就对应着前k个数字里的最小值。 - 紧接着我们尝试用索引区间为 [k, n-1]的数字来更新堆，在这个过程中，只允许比堆顶元素大的值进入堆。这一波操作过后，堆里的
k个数字就是整个数组中最大的k个数字，而堆顶的数字正是这 k 个数中最小的那个。于是本题得解。
我们用示例中的[3,2,1,5,6,4]这个序列来模拟一下上面的过程。初始化一个规模为 k=2 的小顶堆，它长这样：
2/3
用[k, n-1]索引范围内的元素来更新这个小顶堆：首先是用索引为2的数字1来试，发现1比堆顶的2还要小，忽略它。接着用索引为3的5来试，5是比2大的，用它把2换掉：
5/3
经过向下对比+调整，新的堆长这样：
3/5
我们发现，现在这个堆里面保存的正是索引范围[0, 3]内的前 k 个最大的数。以此类推，当对数组中最后一个元素执行过尝试入堆的逻辑后，堆里面保存的就是整个数组范围内的前 k 个最大的数。
在解题的过程中，不出所料地用到了上文中提及的downHeap方法和upHeap 方法。不过大家千万不要直接复制粘贴，别忘了，前面我们是用大顶堆举例，这道题需要构造的是小顶堆——记得调整大小关系规则。
（一切尽在注释中，不要只记得抄代码啊年轻人）
/*** @param {number[]} nums* @param {number} k* @return {number}*/const findKthLargest = function(nums, k) {// 初始化一个堆数组const heap = []// n表示堆数组里当前最后一个元素的索引let n = 0// 缓存 nums 的长度const len = nums.length// 初始化大小为 k 的堆function createHeap() {for(let i=0;i<k;i++) {// 逐个往堆里插入数组中的数字insert(nums[i])}}// 尝试用 [k, n-1] 区间的元素更新堆function updateHeap() {for(let i=k;i<len;i++) {// 只有比堆顶元素大的才有资格进堆if(nums[i]>heap[0]) {// 用较大数字替换堆顶数字heap[0] = nums[i]// 重复向下对比+交换的逻辑downHeap(0, k)}}}// 向下对比函数function downHeap(low, high) {// 入参是堆元素在数组里的索引范围，low表示下界，high表示上界let i=low,j=i*2+1// 当 j 不超过上界时，重复向下对比+交换的操作while(j<=high) {// // 如果右孩子比左孩子更小，则用右孩子和根结点比较if(j+1<=high && heap[j+1]<heap[j]) {j = j+1}// 若当前结点比孩子结点大，则交换两者的位置，把较小的结点“拱上去”if(heap[i] > heap[j]) {// 交换位置const temp = heap[j]heap[j] = heap[i]heap[i] = temp// i 更新为被交换的孩子结点的索引i=j// j 更新为孩子结点的左孩子的索引j=j*2+1} else {break}}}// 入参是堆元素在数组里的索引范围，low表示下界，high表示上界function upHeap(low, high) {// 初始化 i（当前结点索引）为上界let i = high// 初始化 j 为 i 的父结点let j = Math.floor((i-1)/2)// 当 j 不逾越下界时，重复向上对比+交换的过程while(j>=low) {// 若当前结点比父结点小if(heap[j]>heap[i]) {// 交换当前结点与父结点，保持父结点是较小的一个const temp = heap[j]heap[j] = heap[i]heap[i] = temp// i更新为被交换父结点的位置i=j// j更新为父结点的父结点j=Math.floor((i-1)/2)} else {break}}}// 插入操作=将元素添加到堆尾部+向上调整元素的位置function insert(x) {heap[n] = xupHeap(0, n)n++}// 调用createHeap初始化元素个数为k的队createHeap()// 调用updateHeap更新堆的内容，确保最后堆里保留的是最大的k个元素updateHeap()// 最后堆顶留下的就是最大的k个元素中最小的那个，也就是第k大的元素return heap[0]};
编码复盘
上面这个题解中出现的 heap 数组，就是一个优先队列。
优先队列的本质是二叉堆结构，它具有以下特性：
- 队列的头部元素，也即索引为0的元素，就是整个数组里的最值——最大值或者最小值
- 对于索引为
i的元素来说，它的父结点下标是(i-1)/2（上面咱们讲过了，这与完全二叉树的结构特性有关） - 对于索引为
i的元素来说，它的左孩子下标应为2*i+1，右孩子下标应为2*i+2。
当题目中出现类似于“第k大”或者“第k高“这样的关键字时，就是在暗示你用优先队列/堆结构来做题——这样的手法可以允许我们在不对序列进行完全排序的情况下，找到第 k 个最值。
在其它语言的算法面试中，优先队列可以直接借助语言本身提供的数据结构来实现（比如JAVA中的priority_queue）。但在 JS 中，我们只能手动造轮子。因此，优先队列在前端算法面试中的权重并不高。如果本节内容让你感觉学起来有难度，那么也不用灰心，更不必焦虑——把握好下一节开始的排序算法专题，上了考场你仍然是一条好汉。
若有收获，就点个赞吧
0 人点赞
