8 | 字符串的应用——真题归纳与解读

字符串在算法面试中，单独考察的机会并不多，同样倾向于和一些经典算法（后面会讲的）结合来体现区分度。步子不能跨太大，不然容易扯着x。本节我们照样是先解决只需要数据结构知识做基础就可以解决的字符串问题。
在讲题之前，我首先要给大家点拨两个字符串相关的“基本算法技能”。这两个技能偶尔也会单独命题，但整体来看在综合性题目中的考察频率较高，需要大家着重熟悉、反复练习和记忆，确保真正做题时万无一失。

基本算法技能

反转字符串

在 JS 中，反转字符串我们直接调相关 API 即可，相信不少同学都能手到擒来：

// 定义被反转的字符串 
const str = 'juejin'  
// 定义反转后的字符串
const res = str.split('').reverse().join('')
console.log(res) // nijeuj

（这段代码需要你非常熟悉，一些公司一面为了试水，有时会单独考这个操作）。

判断一个字符串是否是回文字符串

回文字符串，就是正着读和倒着读都一🐱一样的字符串，比如这样的：

'yessey'

结合这个定义，我们不难写出一个判定回文字符串的方法：

function isPalindrome(str) {
    // 先反转字符串
    const reversedStr = str.split('').reverse().join('')
    // 判断反转前后是否相等
    return reversedStr === str
}

同时，回文字符串还有另一个特性：如果从中间位置“劈开”，那么两边的两个子串在内容上是完全对称的。因此我们也可以结合对称性来做判断：

function isPalindrome(str) {
    // 缓存字符串的长度
    const len = str.length
    // 遍历前半部分，判断和后半部分是否对称
    for(let i=0;i<len/2;i++) {
        if(str[i]!==str[len-i-1]) {
            return false
        }
    }
    return true
}

（谨记这个对称的特性，非常容易用到）

高频真题解读

回文字符串的衍生问题

真题描述：给定一个非空字符串 s，最多删除一个字符。判断是否能成为回文字符串。 示例 1:

输入: “aba”
输出: True
示例 2:
输入: “abca”
输出: True
解释: 你可以删除c字符。
注意: 字符串只包含从 a-z 的小写字母。字符串的最大长度是50000。

思路分析

这道题很多同学第一眼看过去，可能本能地会想到这样一种解法：若字符串本身不回文，则直接遍历整个字符串。遍历到哪个字符就删除哪个字符、同时对删除该字符后的字符串进行是否回文的判断，看看存不存在删掉某个字符后、字符串能够满足回文的这种情况。
这个思路真的实现起来的话，在判题系统眼里其实也是没啥毛病的。但是在面试官看来，就有点问题了——这不是一个高效的解法。
如何判断自己解决回文类问题的解法是否“高效”？其中一个很重要的标准，就是看你对回文字符串的对称特性利用得是否彻底。
字符串题干中若有“回文”关键字，那么做题时脑海中一定要冒出两个关键字——对称性 和 双指针。这两个工具一起上，足以解决大部分的回文字符串衍生问题。
回到这道题上来，我们首先是初始化两个指针，一个指向字符串头部，另一个指向尾部：

如果两个指针所指的字符恰好相等，那么这两个字符就符合了回文字符串对对称性的要求，跳过它们往下走即可。如果两个指针所指的字符串不等，比如这样：

那么就意味着不对称发生了，意味着这是一个可以“删掉试试看”的操作点。我们可以分别对左指针字符和右指针字符尝试进行“跳过”，看看区间在 [left+1, right] 或 [left, right-1] 的字符串是否回文。如果是的话，那么就意味着如果删掉被“跳过”那个字符，整个字符串都将回文：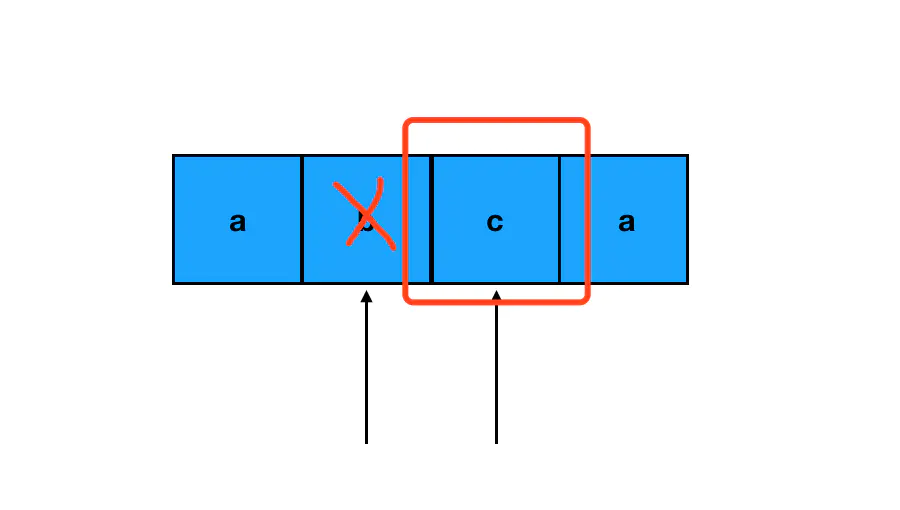
比如说这里我们跳过了 b，[left+1, right] 的区间就是 [2, 2]，它对应 c 这个字符，单个字符一定回文。这样一来，删掉 b 之后，左右指针所指的内部区间是回文的，外部区间也是回文的，可以认为整个字符串就是一个回文字符串了。

编码实现

const validPalindrome = function(s) {
    // 缓存字符串的长度
    const len = s.length
    // i、j分别为左右指针
    let i=0, j=len-1
    // 当左右指针均满足对称时，一起向中间前进
    while(i<j&&s[i]===s[j]) {
        i++ 
        j--
    }
    // 尝试判断跳过左指针元素后字符串是否回文
    if(isPalindrome(i+1,j)) {
      return true
    }
    // 尝试判断跳过右指针元素后字符串是否回文
    if(isPalindrome(i,j-1)) {
        return true
    }
    // 工具方法，用于判断字符串是否回文
    function isPalindrome(st, ed) {
        while(st<ed) {
            if(s[st] !== s[ed]) {
                return false
            }
            st++
            ed--
        } 
        return true
    }
    // 默认返回 false
    return false 
};

字符串匹配问题——正则表达式初相见

接下来我们来看一道综合性比较强的字符串大题：

真题描述： 设计一个支持以下两种操作的数据结构：

void addWord(word)
bool search(word)
search(word) 可以搜索文字或正则表达式字符串，字符串只包含字母 . 或 a-z 。
. 可以表示任何一个字母。

示例:

addWord(“bad”)
addWord(“dad”)
addWord(“mad”)
search(“pad”) -> false
search(“bad”) -> true
search(“.ad”) -> true
search(“b..”) -> true
说明:
你可以假设所有单词都是由小写字母 a-z 组成的。

思路分析

这道题要求字符串既可以被添加、又可以被搜索，这就意味着字符串在添加时一定要被存在某处。键值对存储，我们用 Map（或对象字面量来模拟 Map）。
注意，这里为了降低查找时的复杂度，我们可以考虑以字符串的长度为 key，相同长度的字符串存在一个数组中，这样可以提高我们后续定位的效率。
难点在于 search 这个 API，它既可以搜索文字，又可以搜索正则表达式。因此我们在搜索前需要额外判断一下，传入的到底是普通字符串，还是正则表达式。若是普通字符串，则直接去 Map 中查找是否有这个 key；若是正则表达式，则创建一个正则表达式对象，判断 Map 中相同长度的字符串里，是否存在一个能够与这个正则相匹配。
这里需要大家复习一下正则表达式的创建，以及用于测试某个字符串是否与之匹配的方法：

/**
 * 构造函数
 */
const WordDictionary = function () {
  // 初始化一个对象字面量，承担 Map 的角色
  this.words = {}
};
/**
  添加字符串的方法
 */
WordDictionary.prototype.addWord = function (word) {
  // 若该字符串对应长度的数组已经存在，则只做添加
  if (this.words[word.length]) {
    this.words[word.length].push(word)
  } else {
    // 若该字符串对应长度的数组还不存在，则先创建
    this.words[word.length] = [word]
  }
};
/**
  搜索方法
 */
WordDictionary.prototype.search = function (word) {
  // 若该字符串长度在 Map 中对应的数组根本不存在，则可判断该字符串不存在
  if (!this.words[word.length]) {
    return false
  }
  // 缓存目标字符串的长度
  const len = word.length
  // 如果字符串中不包含‘.’，那么一定是普通字符串
  if (!word.includes('.')) {
    // 定位到和目标字符串长度一致的字符串数组，在其中查找是否存在该字符串
    return this.words[len].includes(word)
  }
  // 否则是正则表达式，要先创建正则表达式对象
  const reg = new RegExp(word)
  // 只要数组中有一个匹配正则表达式的字符串，就返回true
  return this.words[len].some((item) => {
    return reg.test(item)
  })
};

正则表达式更进一步——字符串与数字之间的转换问题

真题描述：请你来实现一个 atoi 函数，使其能将字符串转换成整数。

首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。
当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号；假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成整数。
该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响。
注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换。
在任何情况下，若函数不能进行有效的转换时，请返回 0。

说明：

假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−2^31, 2^31 − 1]。如果数值超过这个范围，请返回 INT_MAX (2^31 − 1) 或 INT_MIN (−2^31) 。

示例 1:

输入: “42”
输出: 42

示例 2:

输入: “ -42”
输出: -42
解释: 第一个非空白字符为 ‘-‘, 它是一个负号。
我们尽可能将负号与后面所有连续出现的数字组合起来，最后得到 -42 。

示例 3:

输入: “4193 with words”
输出: 4193
解释: 转换截止于数字 ‘3’ ，因为它的下一个字符不为数字。

示例 4:

输入: “words and 987”
输出: 0
解释: 第一个非空字符是 ‘w’, 但它不是数字或正、负号。 因此无法执行有效的转换。

示例 5:

输入: “-91283472332”
输出: -2147483648
解释: 数字 “-91283472332” 超过 32 位有符号整数范围。因此返回 INT_MIN (−2^31) 。

思路解读

这道题乍一看比较唬人，毕竟题干这么长，首先会刷掉一波没耐心读完的火大老哥。我在实际的面试情景下，见过题没读完就掀桌走人的…..嗨，这里特别提醒大家，千万别冲动：小孩子才害怕读题，成年人都偷着乐——你得知道，一般来说，题干越长，题目越好做。
为啥这样说？大家想想，我们做题靠的是什么？自身的知识储备+题目提供的信息。题干长意味着什么？意味着它提供的信息相对丰富、细节描述相对到位，甚至很有可能，这个题的答案都藏在题里了！
就拿这道题开刀，我把其中比较关键的句子摘出来给大家翻译翻译：

1. 该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止——暗示你拿到字符串先去空格；
   
2. 当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号——暗示你识别开头的“+”字符和“-”字符；
   
3. 该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响——暗示你见到非整数字符就刹车；
   
4. 说明： 假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−2^31, 2^31 − 1]。如果数值超过这个范围，请返回 INT_MAX (2^31 − 1) 或 INT_MIN (−2^31) ——暗示……这都不是暗示了，这是明示啊！直接告诉你先把这俩边界值算出来，摆在那做卡口就完了。
   

Step1：计算卡口
所以说不管这道题你用啥方法做，这个卡口计算肯定是没跑了。计算某个数的 n 次方，我们要用到 Math.pow 这个方法：

// 计算最大值
const max = Math.pow(2,31) - 1
// 计算最小值
const min = -max - 1

Step2：解析字符串
这道题其实有很多种解法，不同解法之间的区别就在于解析字符串的方式不同。
最直接的解法，是对字符串进行遍历，在遍历的过程中，按照上文我给大家提取的 1、2、3 这三点暗示，逐个地去对每个遍历对象进行判断，从而提取出符合题目要求的数字字符串，再把它转换成数字。
这样做理论上来说没毛病，也不会有超时问题。不过这里我更推荐大家用正则来做，原因很简单：我们看题目里有这么密集的字符串约束条件，作为前端，本能地是能想到用正则来做的；同时，正则表达式本身就是前端面试中的一个基础知识点，如果一道题能够同时考察字符串操作和正则表达式，其实也正中了面试官的下怀。
现在我们决定了用正则来做这道题，能不能做对它，就要看咱们正则表达式能不能写对了。
对于正则表达式，大多数的团队不会有特别强硬的要求，不会期望你一定要多么多么精通、能不靠 Google 徒手写多么复杂的表达式出来啥的——这样搞其实也没有意义。但是必要的基础你是要有的，这道题目涉及到的正则其实就在这个“必要”的范围里，我们一起来分析一下，首先是看回这三个约束条件，我重新给大家翻译一下：

1. 该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止——允许字符串头部出现空格，但是你在处理的时候要想办法把它摘出去，不要让它干扰你的计算
   
2. 当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号——允许字符串的第一个有效字符为“+”或者“—”，不要摘它出去，它对你的计算是有意义的
   
3. 该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响——匹配的时候，连续整数之外的部分都应该被摘除
   

通过以上分析，我们可以形成以下思路：
首先，摘除空格：有两个方法，一个是直接使用 string 的 trim 方法，它是 JavaScript 的一个原生方法，可以去除字符串的头尾空格:

let str = '      +10086'
str.trim() // '+10086'

另一个方法是在匹配的时候，匹配空格（正则匹配符为 \s，意味着匹配 0 个或多个空格），但是*不把它放在捕获组里——这种方法会更加通用，正则表达式匹配过程中，所有的“摘除”动作都可以通过将匹配到的结果排除在捕获组之外来实现，
什么是捕获组？其实就是正则表达式中被小括号括住的部分。在这道题里，我们需要从字符串中提取的其实只有“+/-”符号以及其后面的数字而已，同时这个字符串需要满足 可能存在的空格+正负号+数字字符串+其它字符内容 这样的格式才算合法，那我们就可以通过这样写正则表达式，实现“匹配”和“提取”的双重目的：

/\s*([-\+]?[0-9]*).*/

针对正则基础比较薄弱的同学，我来解释一下上面这个正则表达式：

• 首先，\s 这个符号，意味着空字符，它可以用来匹配回车、空格、换行等空白区域，这里，它用来被匹配空格。*这个符号，跟在其它符号后面，意味着“前面这个符号可以出现0次或多次。\s*，这里的意思就是空格出现0次或多次，都可被匹配到。
• 接着 () 出现了。() 圈住的内容，就是我们要捕获起来额外存储的东西。
• []中的匹配符之间是“或”的关系，也就是说只要能匹配上其中一个就行了。这里[]中包括了-和\+，-不必说匹配的是对应字符，这个\+之所以加了一个斜杠符，是因为+本身是一个有特殊作用的正则匹配符，这里我们要让它回归+字符的本义，所以要用一个\来完成转义。
• [0-9]*结合咱们前面铺陈的知识，这个就不难理解了，它的意思是 0-9 之间的整数，能匹配到0个或多个就算匹配成功。
• 最后的 .这个是任意字符的意思，.*用于字符串尾部匹配非数字的任意字符。我们看到.*是被排除捕获组之外的，所以说这个东西其实也不会被额外存储，它被“摘除”了。

Step3：获取捕获结果
JS 的正则相关方法中， test()方法返回的是一个布尔值，单纯判断“是否匹配”。要想获取匹配的结果，我们需要调度match()方法：

const reg = /\s*([-\+]?[0-9]*).*/
const groups = str.match(reg)

match() 方法是一个在字符串中执行查找匹配的String方法，它返回一个数组，在未匹配到时会返回 null。
如果我们的正则表达式尾部有 g 标志，match()会返回与完整正则表达式匹配的所有结果，但不会返回捕获组。
这里我们没有使用g标志，match()就会返回第一个完整匹配（作为数组的第0项）及其相关的捕获组（作为数组的第1及第1+项）。
这里我们只定义了一个捕获组，因此可以从 groups[1] 里拿到我们捕获的结果。
Step4：判断卡口 最后一步，就是把捕获的结果转换成数字，看看是否超出了题目要求的范围。这一步比较简单，无需多言。

字符串在算法面试中，单独考察的机会并不多，同样倾向于和一些经典算法（后面会讲的）结合来体现区分度。步子不能跨太大，不然容易扯着x。本节我们照样是先解决只需要数据结构知识做基础就可以解决的字符串问题。
在讲题之前，我首先要给大家点拨两个字符串相关的“基本算法技能”。这两个技能偶尔也会单独命题，但整体来看在综合性题目中的考察频率较高，需要大家着重熟悉、反复练习和记忆，确保真正做题时万无一失。

基本算法技能

反转字符串

在 JS 中，反转字符串我们直接调相关 API 即可，相信不少同学都能手到擒来：

// 定义被反转的字符串 
const str = 'juejin'  
// 定义反转后的字符串
const res = str.split('').reverse().join('')
console.log(res) // nijeuj

（这段代码需要你非常熟悉，一些公司一面为了试水，有时会单独考这个操作）。

判断一个字符串是否是回文字符串

回文字符串，就是正着读和倒着读都一🐱一样的字符串，比如这样的：

'yessey'

结合这个定义，我们不难写出一个判定回文字符串的方法：

function isPalindrome(str) {
    // 先反转字符串
    const reversedStr = str.split('').reverse().join('')
    // 判断反转前后是否相等
    return reversedStr === str
}

同时，回文字符串还有另一个特性：如果从中间位置“劈开”，那么两边的两个子串在内容上是完全对称的。因此我们也可以结合对称性来做判断：

function isPalindrome(str) {
    // 缓存字符串的长度
    const len = str.length
    // 遍历前半部分，判断和后半部分是否对称
    for(let i=0;i<len/2;i++) {
        if(str[i]!==str[len-i-1]) {
            return false
        }
    }
    return true
}

（谨记这个对称的特性，非常容易用到）

高频真题解读

回文字符串的衍生问题

真题描述：给定一个非空字符串 s，最多删除一个字符。判断是否能成为回文字符串。 示例 1:

输入: “aba”
输出: True
示例 2:
输入: “abca”
输出: True
解释: 你可以删除c字符。
注意: 字符串只包含从 a-z 的小写字母。字符串的最大长度是50000。

思路分析

这道题很多同学第一眼看过去，可能本能地会想到这样一种解法：若字符串本身不回文，则直接遍历整个字符串。遍历到哪个字符就删除哪个字符、同时对删除该字符后的字符串进行是否回文的判断，看看存不存在删掉某个字符后、字符串能够满足回文的这种情况。
这个思路真的实现起来的话，在判题系统眼里其实也是没啥毛病的。但是在面试官看来，就有点问题了——这不是一个高效的解法。
如何判断自己解决回文类问题的解法是否“高效”？其中一个很重要的标准，就是看你对回文字符串的对称特性利用得是否彻底。
字符串题干中若有“回文”关键字，那么做题时脑海中一定要冒出两个关键字——对称性 和 双指针。这两个工具一起上，足以解决大部分的回文字符串衍生问题。
回到这道题上来，我们首先是初始化两个指针，一个指向字符串头部，另一个指向尾部：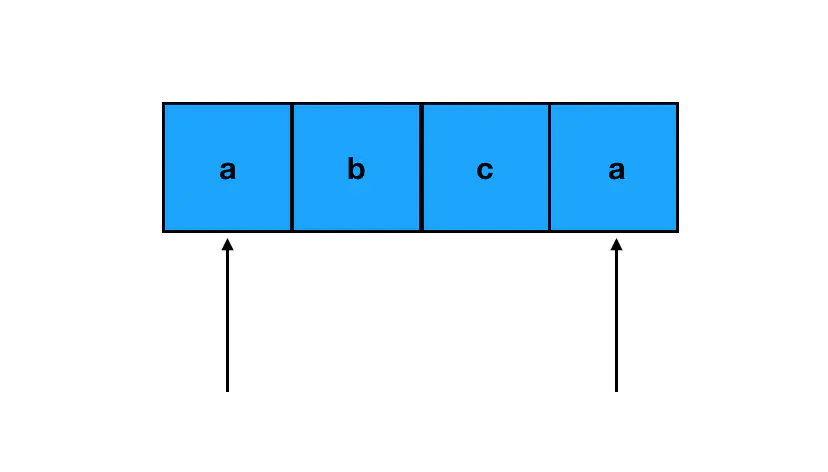

如果两个指针所指的字符恰好相等，那么这两个字符就符合了回文字符串对对称性的要求，跳过它们往下走即可。如果两个指针所指的字符串不等，比如这样：

那么就意味着不对称发生了，意味着这是一个可以“删掉试试看”的操作点。我们可以分别对左指针字符和右指针字符尝试进行“跳过”，看看区间在 [left+1, right] 或 [left, right-1] 的字符串是否回文。如果是的话，那么就意味着如果删掉被“跳过”那个字符，整个字符串都将回文：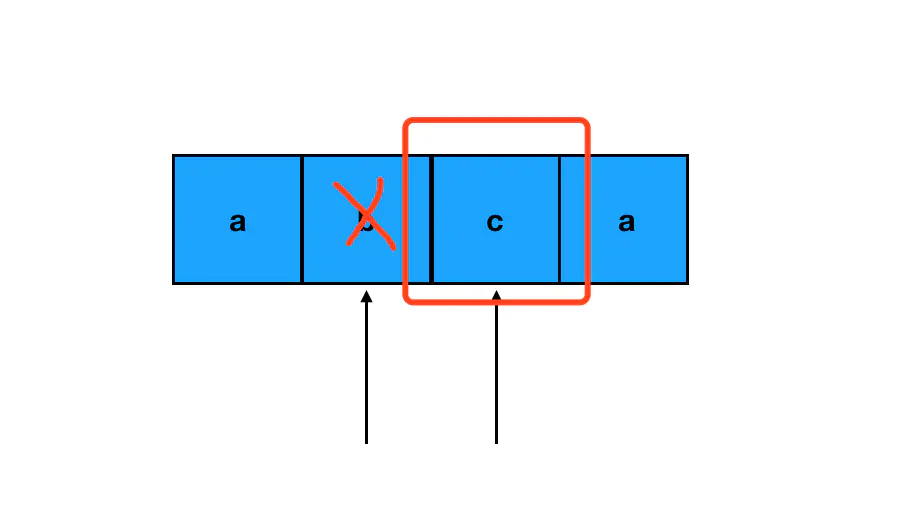
比如说这里我们跳过了 b，[left+1, right] 的区间就是 [2, 2]，它对应 c 这个字符，单个字符一定回文。这样一来，删掉 b 之后，左右指针所指的内部区间是回文的，外部区间也是回文的，可以认为整个字符串就是一个回文字符串了。

编码实现

const validPalindrome = function(s) {
    // 缓存字符串的长度
    const len = s.length
    // i、j分别为左右指针
    let i=0, j=len-1
    // 当左右指针均满足对称时，一起向中间前进
    while(i<j&&s[i]===s[j]) {
        i++ 
        j--
    }
    // 尝试判断跳过左指针元素后字符串是否回文
    if(isPalindrome(i+1,j)) {
      return true
    }
    // 尝试判断跳过右指针元素后字符串是否回文
    if(isPalindrome(i,j-1)) {
        return true
    }
    // 工具方法，用于判断字符串是否回文
    function isPalindrome(st, ed) {
        while(st<ed) {
            if(s[st] !== s[ed]) {
                return false
            }
            st++
            ed--
        } 
        return true
    }
    // 默认返回 false
    return false 
};

字符串匹配问题——正则表达式初相见

接下来我们来看一道综合性比较强的字符串大题：

真题描述： 设计一个支持以下两种操作的数据结构：

void addWord(word)
bool search(word)
search(word) 可以搜索文字或正则表达式字符串，字符串只包含字母 . 或 a-z 。
. 可以表示任何一个字母。

示例:

addWord(“bad”)
addWord(“dad”)
addWord(“mad”)
search(“pad”) -> false
search(“bad”) -> true
search(“.ad”) -> true
search(“b..”) -> true
说明:
你可以假设所有单词都是由小写字母 a-z 组成的。

思路分析

这道题要求字符串既可以被添加、又可以被搜索，这就意味着字符串在添加时一定要被存在某处。键值对存储，我们用 Map（或对象字面量来模拟 Map）。
注意，这里为了降低查找时的复杂度，我们可以考虑以字符串的长度为 key，相同长度的字符串存在一个数组中，这样可以提高我们后续定位的效率。
难点在于 search 这个 API，它既可以搜索文字，又可以搜索正则表达式。因此我们在搜索前需要额外判断一下，传入的到底是普通字符串，还是正则表达式。若是普通字符串，则直接去 Map 中查找是否有这个 key；若是正则表达式，则创建一个正则表达式对象，判断 Map 中相同长度的字符串里，是否存在一个能够与这个正则相匹配。
这里需要大家复习一下正则表达式的创建，以及用于测试某个字符串是否与之匹配的方法：

/**
 * 构造函数
 */
const WordDictionary = function () {
  // 初始化一个对象字面量，承担 Map 的角色
  this.words = {}
};
/**
  添加字符串的方法
 */
WordDictionary.prototype.addWord = function (word) {
  // 若该字符串对应长度的数组已经存在，则只做添加
  if (this.words[word.length]) {
    this.words[word.length].push(word)
  } else {
    // 若该字符串对应长度的数组还不存在，则先创建
    this.words[word.length] = [word]
  }
};
/**
  搜索方法
 */
WordDictionary.prototype.search = function (word) {
  // 若该字符串长度在 Map 中对应的数组根本不存在，则可判断该字符串不存在
  if (!this.words[word.length]) {
    return false
  }
  // 缓存目标字符串的长度
  const len = word.length
  // 如果字符串中不包含‘.’，那么一定是普通字符串
  if (!word.includes('.')) {
    // 定位到和目标字符串长度一致的字符串数组，在其中查找是否存在该字符串
    return this.words[len].includes(word)
  }
  // 否则是正则表达式，要先创建正则表达式对象
  const reg = new RegExp(word)
  // 只要数组中有一个匹配正则表达式的字符串，就返回true
  return this.words[len].some((item) => {
    return reg.test(item)
  })
};

正则表达式更进一步——字符串与数字之间的转换问题

真题描述：请你来实现一个 atoi 函数，使其能将字符串转换成整数。

首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。
当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号；假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成整数。
该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响。
注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换。
在任何情况下，若函数不能进行有效的转换时，请返回 0。

说明：

假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−2^31, 2^31 − 1]。如果数值超过这个范围，请返回 INT_MAX (2^31 − 1) 或 INT_MIN (−2^31) 。

示例 1:

输入: “42”
输出: 42

示例 2:

输入: “ -42”
输出: -42
解释: 第一个非空白字符为 ‘-‘, 它是一个负号。
我们尽可能将负号与后面所有连续出现的数字组合起来，最后得到 -42 。

示例 3:

输入: “4193 with words”
输出: 4193
解释: 转换截止于数字 ‘3’ ，因为它的下一个字符不为数字。

示例 4:

输入: “words and 987”
输出: 0
解释: 第一个非空字符是 ‘w’, 但它不是数字或正、负号。 因此无法执行有效的转换。

示例 5:

输入: “-91283472332”
输出: -2147483648
解释: 数字 “-91283472332” 超过 32 位有符号整数范围。因此返回 INT_MIN (−2^31) 。

思路解读

这道题乍一看比较唬人，毕竟题干这么长，首先会刷掉一波没耐心读完的火大老哥。我在实际的面试情景下，见过题没读完就掀桌走人的…..嗨，这里特别提醒大家，千万别冲动：小孩子才害怕读题，成年人都偷着乐——你得知道，一般来说，题干越长，题目越好做。
为啥这样说？大家想想，我们做题靠的是什么？自身的知识储备+题目提供的信息。题干长意味着什么？意味着它提供的信息相对丰富、细节描述相对到位，甚至很有可能，这个题的答案都藏在题里了！
就拿这道题开刀，我把其中比较关键的句子摘出来给大家翻译翻译：

1. 该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止——暗示你拿到字符串先去空格；
   
2. 当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号——暗示你识别开头的“+”字符和“-”字符；
   
3. 该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响——暗示你见到非整数字符就刹车；
   
4. 说明： 假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−2^31, 2^31 − 1]。如果数值超过这个范围，请返回 INT_MAX (2^31 − 1) 或 INT_MIN (−2^31) ——暗示……这都不是暗示了，这是明示啊！直接告诉你先把这俩边界值算出来，摆在那做卡口就完了。
   

Step1：计算卡口
所以说不管这道题你用啥方法做，这个卡口计算肯定是没跑了。计算某个数的 n 次方，我们要用到 Math.pow 这个方法：

// 计算最大值
const max = Math.pow(2,31) - 1
// 计算最小值
const min = -max - 1

Step2：解析字符串
这道题其实有很多种解法，不同解法之间的区别就在于解析字符串的方式不同。
最直接的解法，是对字符串进行遍历，在遍历的过程中，按照上文我给大家提取的 1、2、3 这三点暗示，逐个地去对每个遍历对象进行判断，从而提取出符合题目要求的数字字符串，再把它转换成数字。
这样做理论上来说没毛病，也不会有超时问题。不过这里我更推荐大家用正则来做，原因很简单：我们看题目里有这么密集的字符串约束条件，作为前端，本能地是能想到用正则来做的；同时，正则表达式本身就是前端面试中的一个基础知识点，如果一道题能够同时考察字符串操作和正则表达式，其实也正中了面试官的下怀。
现在我们决定了用正则来做这道题，能不能做对它，就要看咱们正则表达式能不能写对了。
对于正则表达式，大多数的团队不会有特别强硬的要求，不会期望你一定要多么多么精通、能不靠 Google 徒手写多么复杂的表达式出来啥的——这样搞其实也没有意义。但是必要的基础你是要有的，这道题目涉及到的正则其实就在这个“必要”的范围里，我们一起来分析一下，首先是看回这三个约束条件，我重新给大家翻译一下：

1. 该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止——允许字符串头部出现空格，但是你在处理的时候要想办法把它摘出去，不要让它干扰你的计算
   
2. 当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号——允许字符串的第一个有效字符为“+”或者“—”，不要摘它出去，它对你的计算是有意义的
   
3. 该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响——匹配的时候，连续整数之外的部分都应该被摘除
   

通过以上分析，我们可以形成以下思路：
首先，摘除空格：有两个方法，一个是直接使用 string 的 trim 方法，它是 JavaScript 的一个原生方法，可以去除字符串的头尾空格:

let str = '      +10086'
str.trim() // '+10086'

另一个方法是在匹配的时候，匹配空格（正则匹配符为 \s，意味着匹配 0 个或多个空格），但是*不把它放在捕获组里——这种方法会更加通用，正则表达式匹配过程中，所有的“摘除”动作都可以通过将匹配到的结果排除在捕获组之外来实现，
什么是捕获组？其实就是正则表达式中被小括号括住的部分。在这道题里，我们需要从字符串中提取的其实只有“+/-”符号以及其后面的数字而已，同时这个字符串需要满足 可能存在的空格+正负号+数字字符串+其它字符内容 这样的格式才算合法，那我们就可以通过这样写正则表达式，实现“匹配”和“提取”的双重目的：

/\s*([-\+]?[0-9]*).*/

针对正则基础比较薄弱的同学，我来解释一下上面这个正则表达式：

• 首先，\s 这个符号，意味着空字符，它可以用来匹配回车、空格、换行等空白区域，这里，它用来被匹配空格。*这个符号，跟在其它符号后面，意味着“前面这个符号可以出现0次或多次。\s*，这里的意思就是空格出现0次或多次，都可被匹配到。
• 接着 () 出现了。() 圈住的内容，就是我们要捕获起来额外存储的东西。
• []中的匹配符之间是“或”的关系，也就是说只要能匹配上其中一个就行了。这里[]中包括了-和\+，-不必说匹配的是对应字符，这个\+之所以加了一个斜杠符，是因为+本身是一个有特殊作用的正则匹配符，这里我们要让它回归+字符的本义，所以要用一个\来完成转义。
• [0-9]*结合咱们前面铺陈的知识，这个就不难理解了，它的意思是 0-9 之间的整数，能匹配到0个或多个就算匹配成功。
• 最后的 .这个是任意字符的意思，.*用于字符串尾部匹配非数字的任意字符。我们看到.*是被排除捕获组之外的，所以说这个东西其实也不会被额外存储，它被“摘除”了。

Step3：获取捕获结果
JS 的正则相关方法中， test()方法返回的是一个布尔值，单纯判断“是否匹配”。要想获取匹配的结果，我们需要调度match()方法：

const reg = /\s*([-\+]?[0-9]*).*/
const groups = str.match(reg)

match() 方法是一个在字符串中执行查找匹配的String方法，它返回一个数组，在未匹配到时会返回 null。
如果我们的正则表达式尾部有 g 标志，match()会返回与完整正则表达式匹配的所有结果，但不会返回捕获组。
这里我们没有使用g标志，match()就会返回第一个完整匹配（作为数组的第0项）及其相关的捕获组（作为数组的第1及第1+项）。
这里我们只定义了一个捕获组，因此可以从 groups[1] 里拿到我们捕获的结果。
Step4：判断卡口 最后一步，就是把捕获的结果转换成数字，看看是否超出了题目要求的范围。这一步比较简单，无需多言。