本节我们学习两种关键的基本算法思想:DFS(深度优先搜索)和BFS(广度优先搜索)。这两种算法和栈、队列有着千丝万缕的关系,如果前两节你认真学习掌握了,那么这一节对你来说相信不是问题。
深度优先搜索思想:不撞南墙不回头的“迷宫游戏”
20世纪90年代,小霸王学习机风靡全国。没有哪个小学生,不想拥有一台自己的小霸王学习机——我,也不例外;没有哪个小学生在拥有了小霸王学习机之后,会真的用它来搞学习——我,也不例外。在那个没有王者也没有吃鸡的年代里,小霸王里让我欲罢不能的除了魂斗罗、超级玛丽,还有它——迷宫游戏:
很多同学跟我说他入门算法的时候就挂在 DFS 这里,觉得太高深了,学不动。傻孩子,今天你就会知道,深度优先搜索也不过是在用编码的方式玩一场迷宫游戏。
现在把图上的小黄点想象成你自己,由于你手里没有地图、没有无人机,因此你对迷宫整体的地形一无所知。放眼望去,你眼前只有冰冷的墙壁和并不知道能不能走通的道路。如何走出一条通路?你只能尝试把每一条能走的路都走一遍——也就是所谓的“穷举法”:
- 以当前位置为起点,闷头往前走
- 在前进的过程中,难免会遇到岔路口。这个路口可能分叉出去两条、三条、四条甚至更多的道路,你只能选择其中的一条路、然后继续前进(注意,你可能会不止一次遇到岔路口;每遇到一个新的岔路口,你都需要做一次选择)。
- 你选择的这条路未必是一条通路。如果你走到最后发现此路不通,那么你就要退回到离你最近的那个分叉路口,然后尝试看其它的岔路能不能走通。如果当前的岔路口分叉出去的所有道路都走不通,那么就需要退回到当前岔路口的上一个岔路口,进一步去寻找新的路径。
按照这个思路走下去,只要迷宫是有出口的,你就一定能找到这个出口。在这个过程里,我们贯彻了“不撞南墙不回头”的原则:只要没有碰壁,就决不选择其它的道路,而是坚持向当前道路的深处挖掘——像这样将“深度”作为前进的第一要素的搜索方法,就是所谓的“深度优先搜索”。
深度优先搜索的核心思想,是试图穷举所有的完整路径。
深度优先搜索的本质——栈结构
那么如何使用编码来实现深度优先搜索呢?我们继续讨论迷宫问题,这里我给大家一个抽象过后的简单迷宫结构: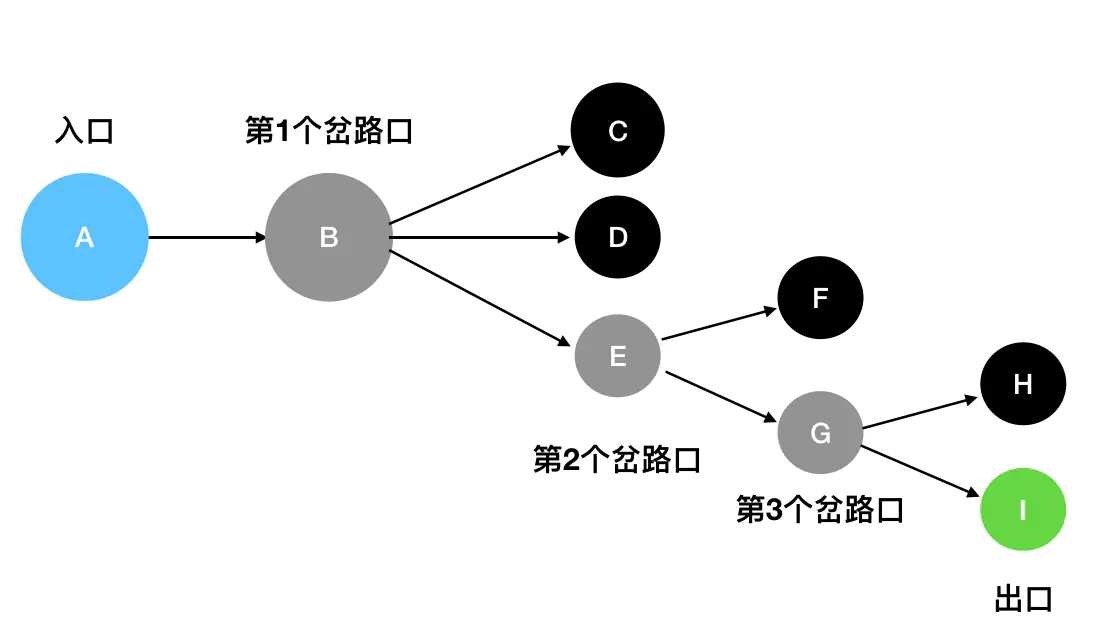
图中蓝色的是入口,灰色的是岔路口,黑色的是死胡同,绿色的是出口。
基于眼前的这个迷宫结构,我们来一步一步模拟一下深度优先搜索的具体过程:
- 从
A出发,沿着唯一的一条道路往下走,遇到了第1个岔路口B。眼前有三个选择:C、D、E。这里我按照从上到下的顺序来走(你也可以按照其它顺序),先走C。 - 发现
C是死胡同,后退到最近的岔路口B,尝试往D方向走。 - 发现
D是死胡同,,后退到最近的岔路口B,尝试往E方向走。 E是一个岔路口,眼前有两个选择:F和G。按照从上到下的顺序来走,先走F。- 发现
F是死胡同,后退到最近的岔路口E,尝试往G方向走。 G是一个岔路口,眼前有两个选择:H和I。按照从上到下的顺序来走,先走H。- 发现
H是死胡同,后退到最近的岔路口G,尝试往I方向走。 I就是出口,成功走出迷宫。
大家观察一下这个过程,会不会觉得这些前进、后退的操作,其实和栈结构的入栈、出栈过程非常相似呢?
现在我们把迷宫中的每一个坐标看做是栈里的一个元素,用栈来模拟这个过程:
- 从
A出发(A入栈),经过了B(B入栈),接下来面临C、D、E三条路。这里按照从上到下的顺序来走(你也可以选择其它顺序),先走C(C入栈)。 - 发现
C是死胡同,后退到最近的岔路口B(C出栈),尝试往D方向走(D入栈)。 - 发现
D是死胡同,,后退到最近的岔路口B(D出栈),尝试往E方向走(E入栈)。 E是一个岔路口,眼前有两个选择:F和G。按照从上到下的顺序来走,先走F(F入栈)。- 发现
F是死胡同,后退到最近的岔路口E(F出栈),尝试往G方向走(G入栈)。 G是一个岔路口,眼前有两个选择:H和I。按照从上到下的顺序来走,先走H(H入栈)。- 发现
H是死胡同,后退到最近的岔路口G(H出栈),尝试往I方向走(I入栈)。 I就是出口,成功走出迷宫。
此时栈里面的内容就是A、B、E、G、I,因此 A->B->E->G->I 就是走出迷宫的路径。通过深度优先搜索,我们不仅可以定位到迷宫的出口,还可以记录下相关的路径信息。
现在大家知道了深度优先搜索的过程可以转化为一系列的入栈、出栈操作。那么深度优先搜索在编码上一般会如何实现呢?这里,就需要大家回忆一下第 5 节的内容了——DFS 中,我们往往使用递归来模拟入栈、出栈的逻辑。
DFS 与二叉树的遍历
现在我们站在深度优先搜索的角度,重新理解一下二叉树的先序遍历过程: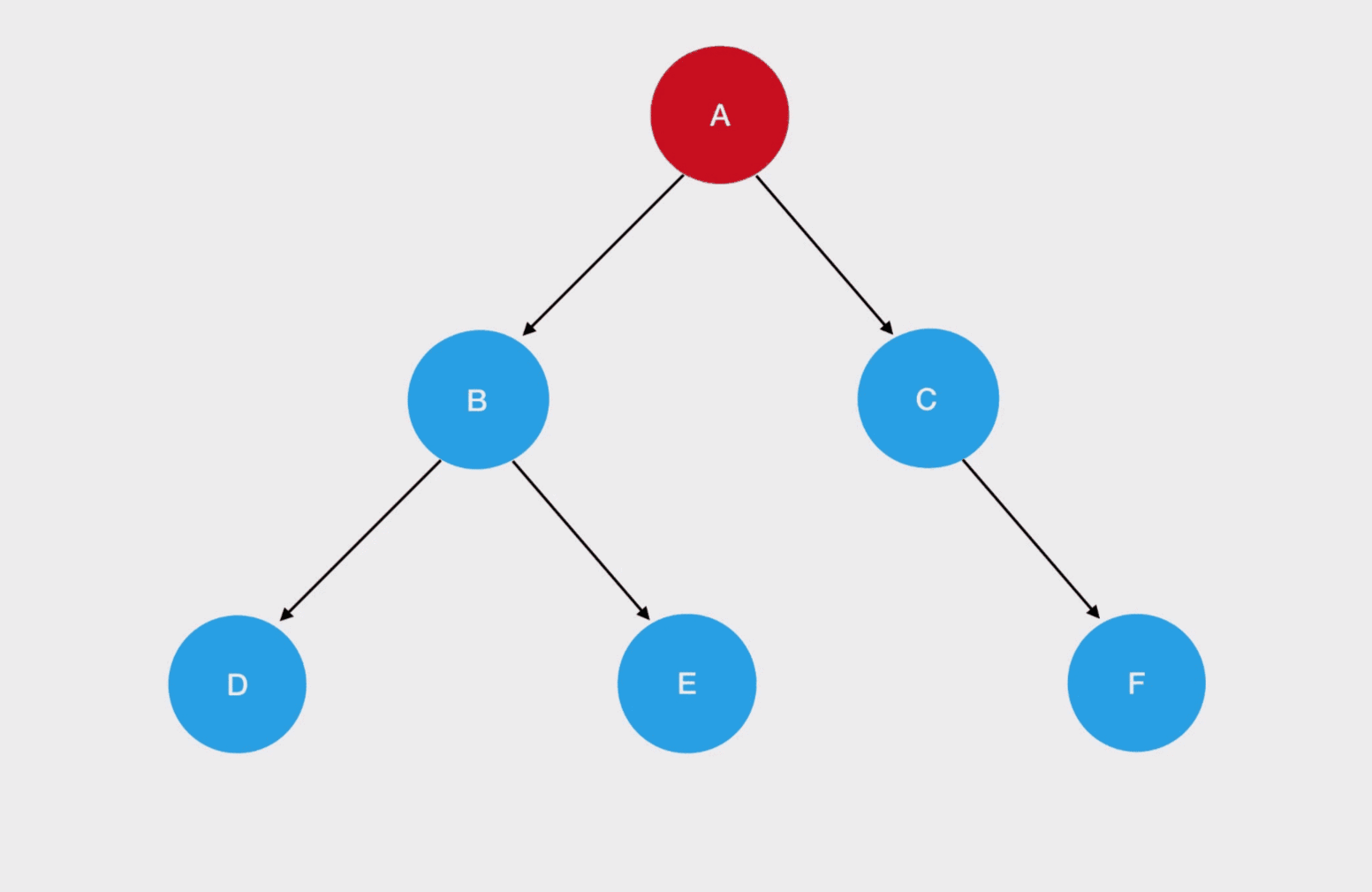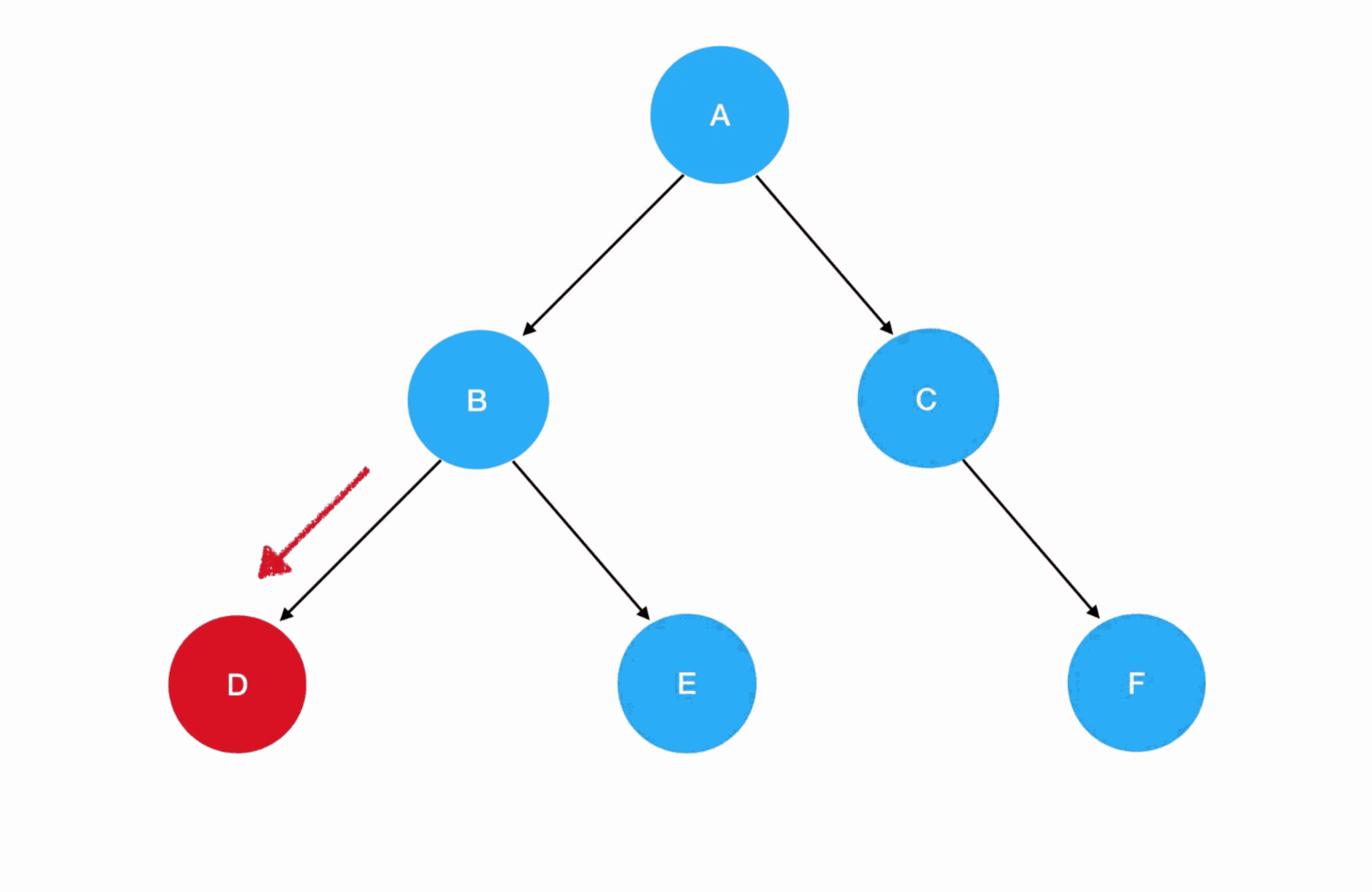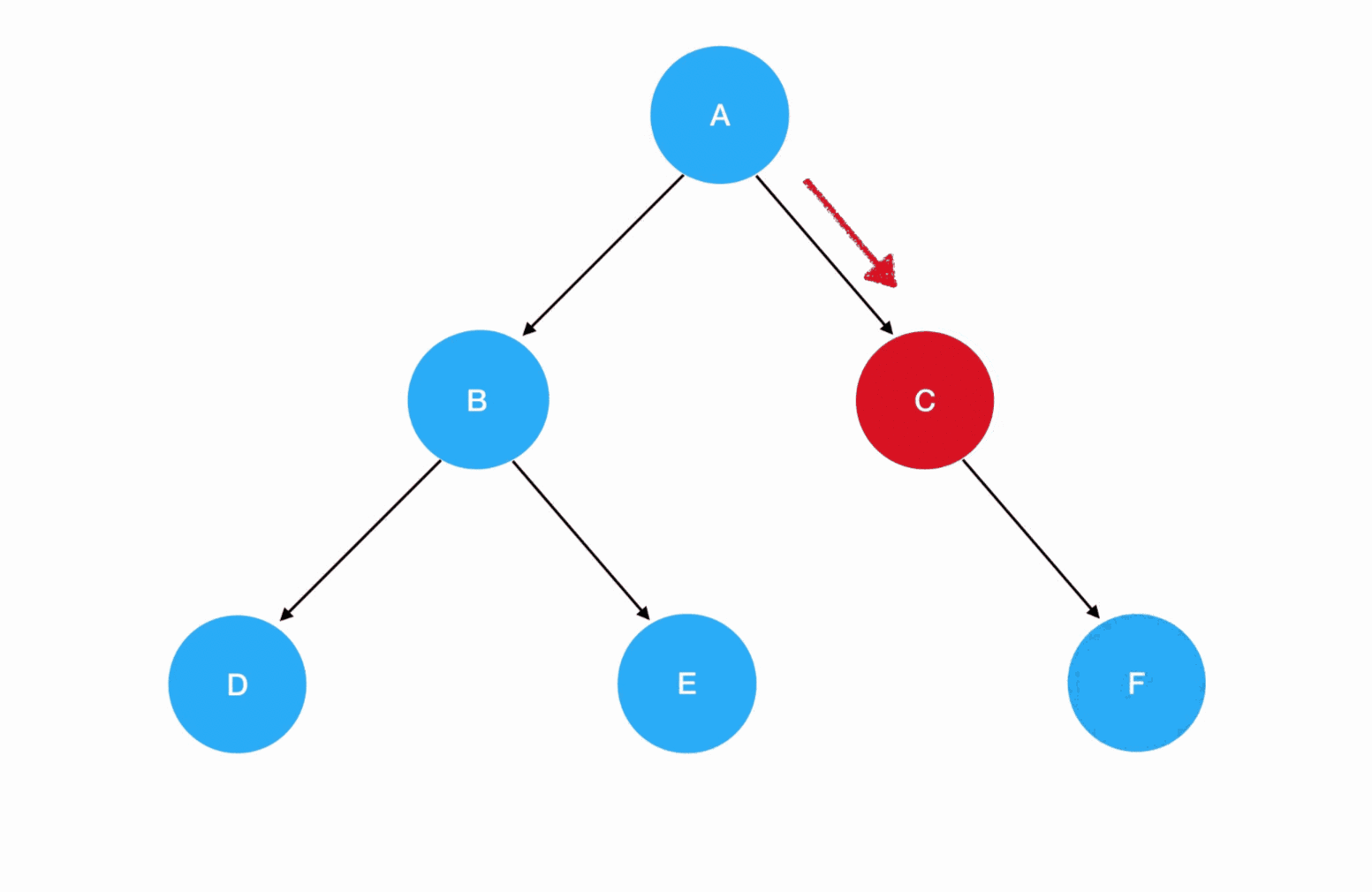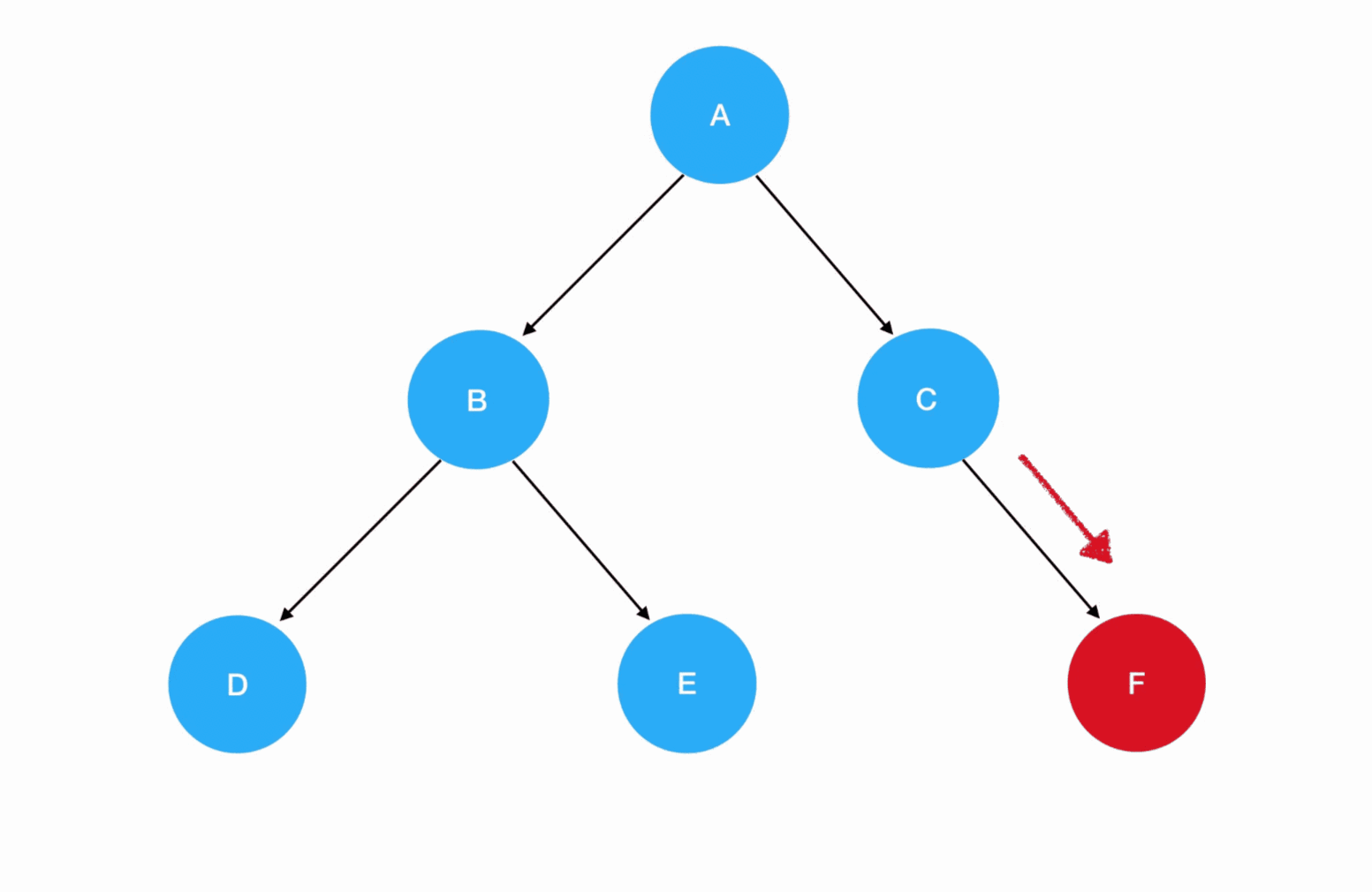
从 A 结点出发,访问左侧的子结点;如果左子树同样存在左侧子结点,就头也不回地继续访问下去。一直到左侧子结点为空时,才退回到距离最近的父结点、再尝试去访问父结点的右侧子结点——这个过程,和走迷宫是何其相似!事实上,在二叉树中,结点就好比是迷宫里的坐标,图中的每个结点在作为父结点时无疑是岔路口,而空结点就是死胡同。我们回顾一下二叉树先序遍历的编码实现:
// 所有遍历函数的入参都是树的根结点对象function preorder(root) {// 递归边界,root 为空if(!root) {return}// 输出当前遍历的结点值console.log('当前遍历的结点值是:', root.val)// 递归遍历左子树preorder(root.left)// 递归遍历右子树preorder(root.right)}
在这个递归函数中,递归式用来先后遍历左子树、右子树(分别探索不同的道路),递归边界在识别到结点为空时会直接返回(撞到了南墙)。因此,我们可以认为,递归式就是我们选择道路的过程,而递归边界就是死胡同。二叉树的先序遍历正是深度优先搜索思想的递归实现。可以说深度优先搜索过程就类似于树的先序遍历、是树的先序遍历的推广。
这时候,可能有同学会有疑问:在二叉树遍历的递归实现里,完全没有栈的影子——这东西似乎和栈没有什么直接联系啊,为啥咱们还说深度优先搜索的本质是栈呢?
我们从两个角度来理解这个事情:
- 首先,函数调用的底层,仍然是由栈来实现的。JS 会维护一个叫“函数调用栈”的东西,
preorder每调用一次自己,相关调用的上下文就会被push进函数调用栈中;待函数执行完毕后,对应的上下文又会从调用栈中被pop出来。因此,即便二叉树的递归调用过程中,并没有出现栈这种数据结构,也依然改变不了递归的本质是栈的事实。 - 其次,DFS 作为一种思想,它和树的递归遍历一脉相承、却并不能完全地画上等号——DFS 的解题场景其实有很多,其中有一类会要求我们记录每一层递归式里路径的状态,此时就会强依赖栈结构(这一点会在下一节的真题实战中体现得淋漓尽致)。
基于上述的两个例子,相信大家已经对深度优先搜索的思想和实现思路形成了自己的理解。本节我们着重理解概念,不急着做题——深度优先搜索的应用是非常广泛的,在后续的小节中,大家自然会见到许许多多使用递归来实现深度优先搜索的实战案例。
广度优先搜索思想——找到迷宫出口的另一种思路
我们回头再来看看这个迷宫结构: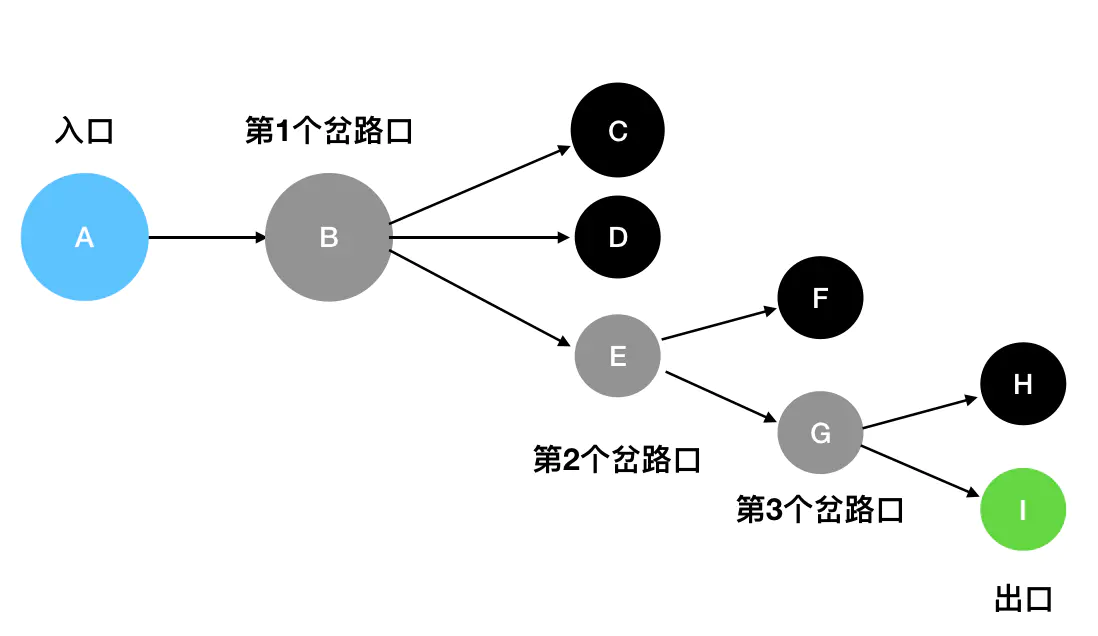
当我们使用深度优先搜索来寻找迷宫出口时,会走出图示这样一条一条的完整路径: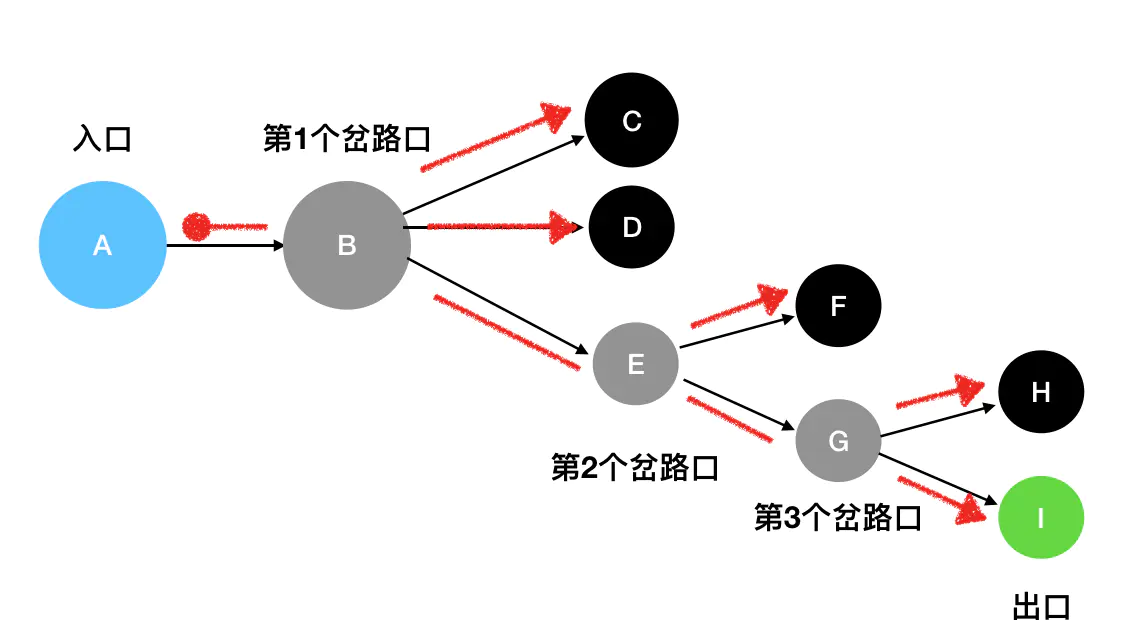
其中红色的圆点意味着路径的起点,红色箭头意味着路径的终点。我们看到从起点开始,一共探索出了 5 条完整的路径。
与深度优先搜索不同的是,广度优先搜索(BFS)并不执着于“一往无前”这件事情。它关心的是眼下自己能够直接到达的所有坐标,其动作有点类似于“扫描”——比如说站在 B 这个岔路口,它会只关注 C、D、E 三个坐标,至于 F、G、H、I这些遥远的坐标,现在不在它的关心范围内: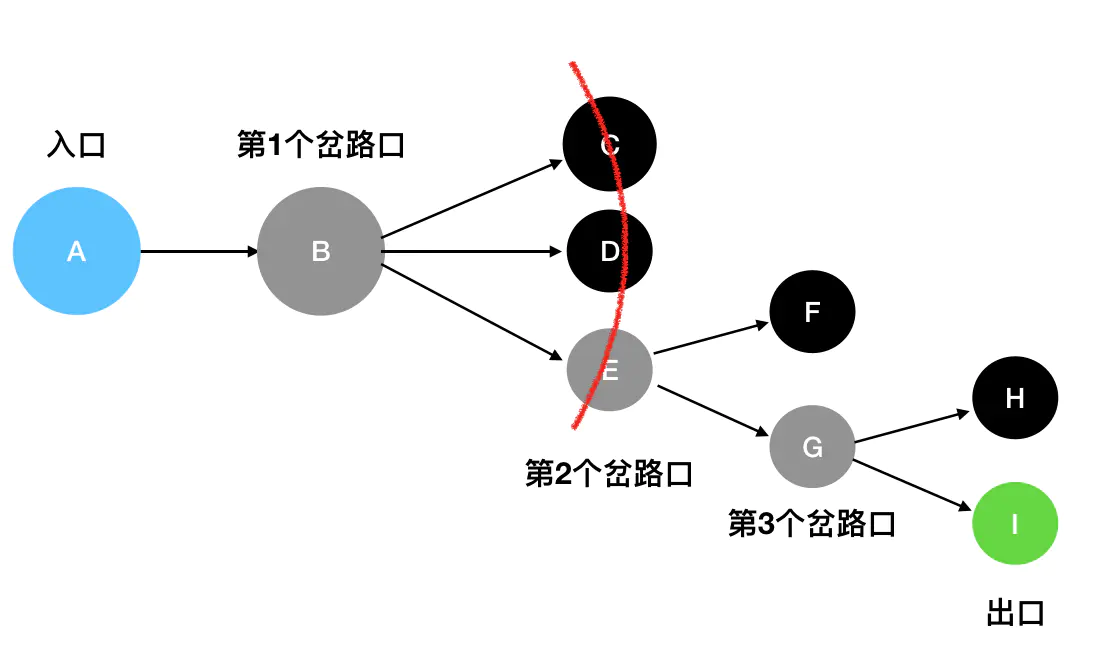
只有在走到了 E处时,它发现此时可以触达的坐标变成了 F、G,此时才会去扫描F、G: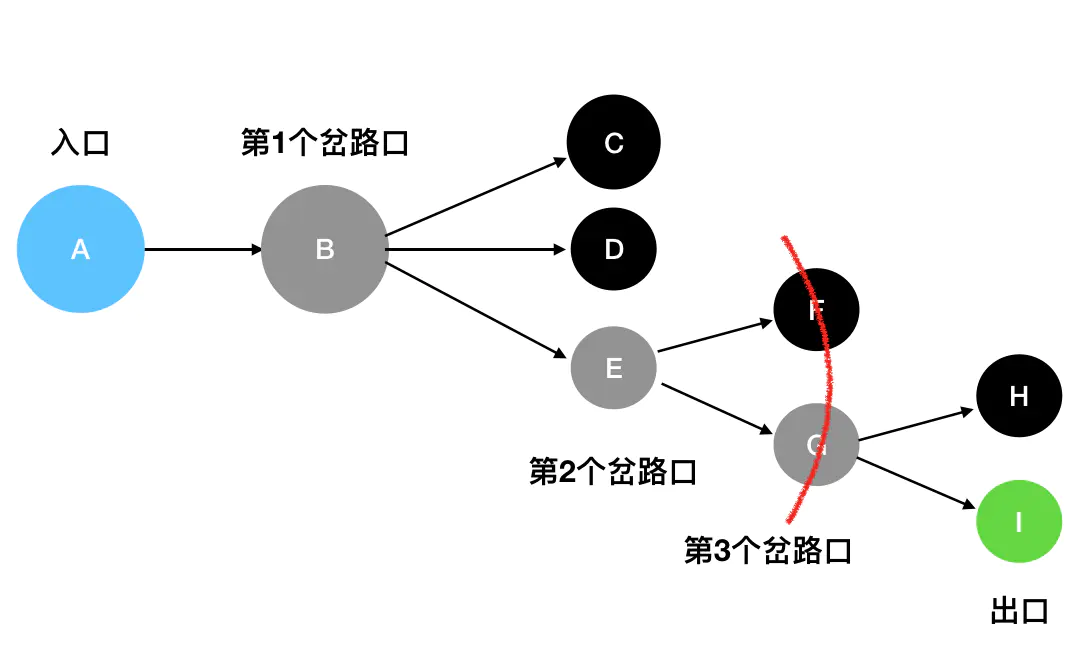
按照这个思路,广度优先搜索每次以“广度”为第一要务、雨露均沾,一层一层地扫描,最后也能够将所有的坐标扫描完全: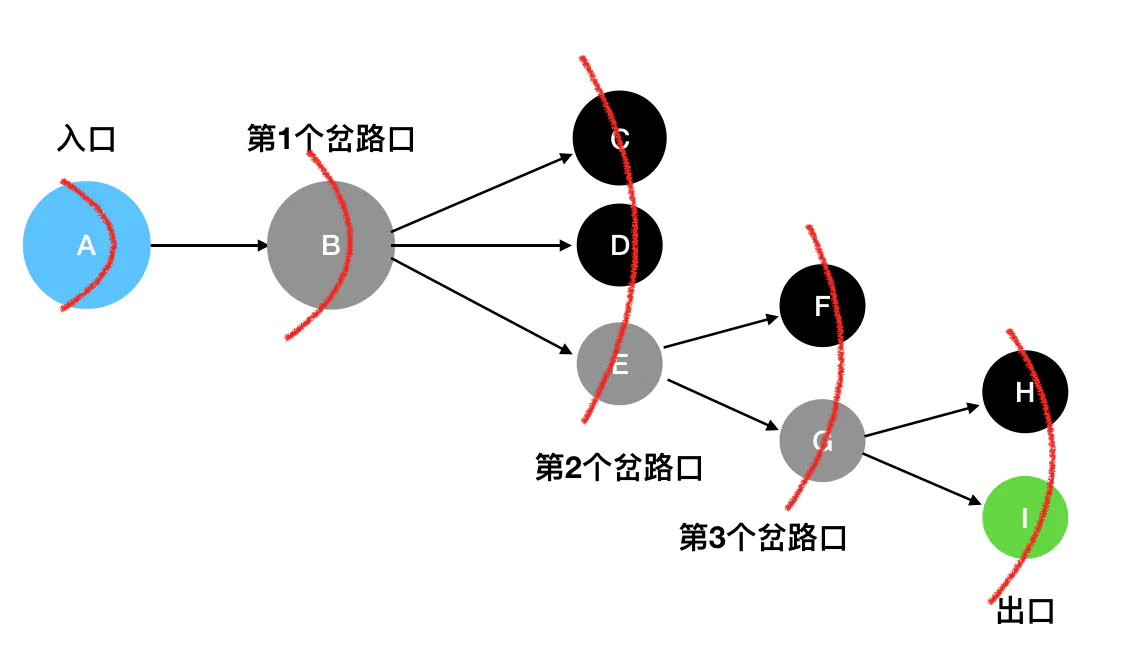
当扫描到 I 的时候,发现 I 是出口,照样能够找到答案。
按照 BFS 的遍历规则,具体的访问步骤会变成下面这样:
- 站在入口
A处(第一层),发现直接能抵达的坐标只有B,于是接下来需要访问的就是B。 - 入口
A访问完毕,走到B处(第二层),发现直接能抵达的坐标变成了C、D和E,于是把这三个坐标记为下一层的访问对象。 B访问完毕,访问第三层。这里我按照从上到下的顺序(你也可以按照其它顺序),先访问C和D,然后访问E。站在C处和D处都没有见到新的可以直接抵达的坐标,所以不做额外的动作。但是在E处见到了可以直接抵达的F和G,因此把F和G记为下一层(第四层)需要访问的对象。- 第三层访问完毕,访问第四层。第四层按照从上到下的顺序,先访问的是
F。从F出发没有可以直接触达的坐标,因此不做额外的操作。接着访问G,发现从G出发可以直接抵达H和I,因此把H和I记为下一层(第五层)需要访问的对象。 - 第四层访问完毕,访问第五层。第五层按照从上到下的顺序,先访问的是
H,发现从H出发没有可以直接抵达的坐标,因此不作额外的操作。接着访问I,发现I就是出口,问题得解。
当然啦,这个问题若采用 BFS 的思路来解,那么它其实已经不能说是一个严格的迷宫游戏了——在一个真正的迷宫游戏里,大概率并不会允许我们如此顺利地逐个访问身在同一层次的所有坐标(比如C和D之间可能就会隔了厚厚的一堵墙,导致你无法在访问C后直接去访问D)。这里我们基于迷宫游戏,抽象出来的其实是一个更为简单的模型。大家不必拘泥于游戏本身,而应该着重理解这个分层遍历的过程。
在分层遍历的过程中,大家会发现两个规律:
- 每访问完毕一个坐标,这个坐标在后续的遍历中都不会再被用到了,也就是说它可以被丢弃掉。
- 站在某个确定坐标的位置上,我们所观察到的可直接抵达的坐标,是需要被记录下来的,因为后续的遍历还要用到它们。
丢弃已访问的坐标、记录新观察到的坐标,这个顺序毫无疑问符合了“先进先出”的原则,因此整个 BFS 算法的实现过程,和队列有着密不可分的关系。
下面我用一个队列 queue 来模拟一下上面的过程:
- 初始化,先将入口
A入队(queue里现在只有A)。 - 访问入口
A(第一层),访问完毕后将A出队。发现直接能抵达的坐标只有B,于是将B入队(queue里现在只有B)。 - 访问
B(第二层),访问完毕后将B出队。发现直接能抵达的坐标变成了C、D和E,于是把这三个坐标记为下一层的访问对象,也就是把它们全部入队(queue里现在是C、D、E) - 访问第三层。这里我按照从上到下的顺序(你也可以按照其它顺序),先访问
C(访问完毕后C出队)和D(访问完毕后D出队),然后访问E(访问完毕后E出队)。访问C处和D处都没有见到新的可以直接抵达的坐标,所以不做额外的动作。但是在E处我们见到了可以直接抵达的F和G,因此把F和G记为下一层(第四层)需要访问的对象,F、G依次入队(queue里现在是F、G)。 - 访问第五层。第五层按照从上到下的顺序,先访问的是
H(访问完毕后H出队),发现从H出发没有可以直接抵达的坐标,因此不作额外的操作。接着访问I(访问完毕后I出队),发现I就是出口,问题得解(此时queue队列已经被清空)。
在这个过程里,我们其实循环往复地做了以下事情:
依次访问队列里已经有的坐标,将其出队;记录从当前坐标出发可直接抵达的所有坐标,将其入队。
以上逻辑用伪代码表述如下:
function BFS(入口坐标) {const queue = [] // 初始化队列queue// 入口坐标首先入队queue.push(入口坐标)// 队列不为空,说明没有遍历完全while(queue.length) {const top = queue[0] // 取出队头元素访问 top // 此处是一些和 top 相关的逻辑,比如记录它对应的信息、检查它的属性等等// 注意这里也可以不用 for 循环,视题意而定for(检查 top 元素出发能够遍历到的所有元素) {queue.push(top能够直接抵达的元素)}queue.shift() // 访问完毕。将队头元素出队}}
注意,理论上来说只要我们拿到了 top,那么就不再关心队头元素了。因此这个 shift 出队的过程,其实是比较灵活的。一般只要我们拿到了 top,就可以执行 shift了。一些同学习惯于把top元素的访问和出队放在一起来做:
const top = queue.shift()
这样做也是没问题的(除非题目中对出队的时机有强约束,但这种情况非常少见)。
BFS实战:二叉树的层序遍历
大家现在回顾一下我们在第 5 节展示过的这个二叉树实例: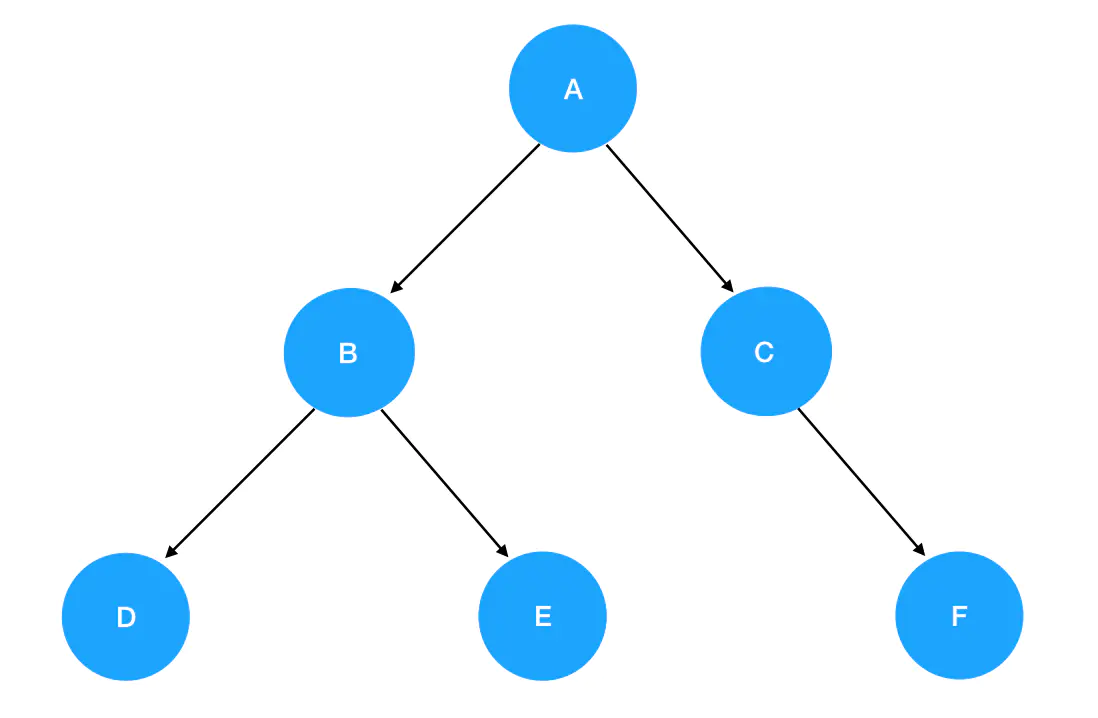
这棵二叉树的编码实现如下:
const root = {val: "A",left: {val: "B",left: {val: "D"},right: {val: "E"}},right: {val: "C",right: {val: "F"}}};
现在我们要做的是对这个二叉树进行层序遍历。层序遍历的概念很好理解:按照层次的顺序,从上到下,从左到右地遍历一个二叉树,如图所示(红色数字即为遍历的序号):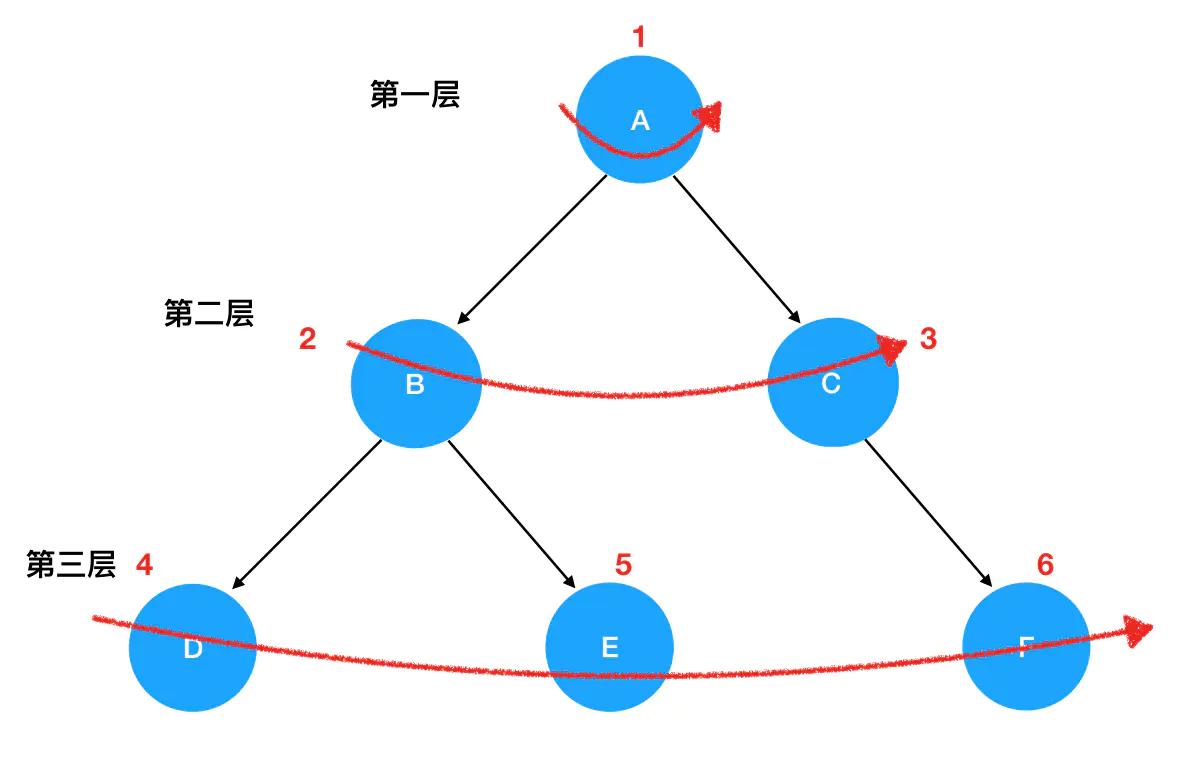
正确的遍历序列为:
ABCDEF
看到“层次”关键字,大家应该立刻想到“扫描”;想到“扫描”,就应该立刻想到 BFS。因此层序遍历,我们就用 BFS 的思路来实现。这里咱们可以直接套用上面的伪代码:
function BFS(root) {const queue = [] // 初始化队列queue// 根结点首先入队queue.push(root)// 队列不为空,说明没有遍历完全while(queue.length) {const top = queue[0] // 取出队头元素// 访问 topconsole.log(top.val)// 如果左子树存在,左子树入队if(top.left) {queue.push(top.left)}// 如果右子树存在,右子树入队if(top.right) {queue.push(top.right)}queue.shift() // 访问完毕,队头元素出队}}
执行 BFS:
BFS(root)
结语
经过本节的学习,相信大家对 DFS、BFS 的核心思想及实现方法都有了比较扎实的掌握。这两种算法在我们今后的做题过程中会反复出现,彼时大家会对它们的应用场景有更加深刻的认知。


