栈与队列相关的问题就比较微妙了，很多时候相关题目中压根不会出现“栈”、“队列”这样的关键字，但只要你深入到真题里去、对栈和队列的应用场景建立起正确的感知，那么很多线索都会在分析的过程中被你轻松地挖掘出来。
这里也和大家分享一位读者在试读过程中的学习感悟：

感觉算法题除了理解还要靠练习，就像高考数学题，要锻炼出解题常规思维。任重道远啊🙊

其实就是这么回事，这也正是我们开篇就跟大家指明“以题为纲”这条路的初衷。
好啦，开工了老哥们！

典型真题快速上手-“有效括号”问题

题目描述：给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串，判断字符串是否有效。 有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。

示例 1:

输入: “()”
输出: true

示例 2:

输入: “()[]{}”
输出: true

示例 3:

输入: “(]”
输出: false

示例 4:

输入: “([)]”
输出: false
示例 5:
输入: “{[]}”
输出: true

思路分析

括号问题在面试中出现频率非常高， 这类题目我们一般首选用栈来做。
为什么可以用栈做？大家想想，括号成立意味着什么？意味着对称性。
巧了，根据栈的后进先出原则，一组数据的入栈和出栈顺序刚好是对称的。比如说1、2、3、4、5、6按顺序入栈，其对应的出栈序列就是 6、5、4、3、2、1：

  1. 123456
  2. 654321

对称关系一目了然。
因此这里大家可以记下一个规律：题目中若涉及括号问题，则很有可能和栈相关。
回到题目中来，我们的思路就是在遍历字符串的过程中，往栈里 push 括号对应的配对字符。比如如果遍历到了 (，就往栈里 push )。
假如字符串中所有的括号都成立，那么前期我们 push 进去的一定全都是左括号、后期 push 进去的一定全都是右括号。而且左括号的入栈顺序，和其对应的右括号的入栈顺序应该是相反的，比如这个例子：

  1. ({[]})

最后一个入栈的左方括号[，与之匹配的右方括号]正是接下来第一个入栈的右括号。
因此，我们可以果断地认为在左括号全部入栈结束时，栈顶的那个左括号，就是第一个需要被配对的左括号。此时我们需要判断的是接下来入栈的第一个右括号是否和此时栈顶的左括号配对。如果配对成功，那么这一对括号就是有效的，否则直接 return false。
当判断出一对有效的括号之后，我们需要及时地丢掉它，去判断其它括号是否有效。这里这个“丢掉”的动作，就对应着两个括号一起出栈的过程。
每配对成功一对括号，我们都将这对括号出栈。这样一来，我们就可以确保栈顶的括号总是下一个需要被匹配的左括号。
如果说我们出栈到最后，栈不为空，那么意味着一部分没有被匹配上的括号被剩下来了，说明字符串中并非所有的括号都有效，判断 false；反之，则说明所有的括号都配对成功了，判断为 true。

编码实现

  1. // 用一个 map 来维护左括号和右括号的对应关系
  2. const leftToRight = {
  3.   "(": ")",
  4.   "[": "]",
  5.   "{": "}"
  6. };
  7. /**
  8.  * @param {string} s
  9.  * @return {boolean}
  10.  */
  11. const isValid = function(s) {
  12.   // 结合题意，空字符串无条件判断为 true
  13.   if (!s) {
  14.     return true;
  15.   }
  16.   // 初始化 stack 数组
  17.   const stack = [];
  18.   // 缓存字符串长度
  19.   const len = s.length;
  20.   // 遍历字符串
  21.   for (let i = 0; i < len; i++) {
  22.     // 缓存单个字符
  23.     const ch = s[i];
  24.     // 判断是否是左括号，这里我为了实现加速，没有用数组的 includes 方法，直接手写判断逻辑
  25.     if (ch === "(" || ch === "{" || ch === "[") stack.push(leftToRight[ch]);
  26.     // 若不是左括号，则必须是和栈顶的左括号相配对的右括号
  27.     else {
  28.       // 若栈不为空，且栈顶的左括号没有和当前字符匹配上，那么判为无效
  29.       if (!stack.length || stack.pop() !== ch) {
  30.         return false;
  31.       }
  32.     }
  33.   }
  34.   // 若所有的括号都能配对成功，那么最后栈应该是空的
  35.   return !stack.length;
  36. };

栈问题进阶-每日温度问题

题目描述: 根据每日气温列表，请重新生成一个列表，对应位置的输出是需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高，请在该位置用 0 来代替。 例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。 提示：气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度，都是在 [30, 100] 范围内的整数。

思路分析

看到这道题，大家不难想到暴力遍历法：直接两层遍历，第一层定位一个温度，第二层定位离这个温度最近的一次升温是哪天，然后求出两个温度对应索引的差值即可。
一个数组两层遍历，属于比较少见且高危的操作。事出反常必有妖，此时我们就需要反思：这道题是不是压根不该用暴力遍历来做？
答案是肯定的。因为在这个暴力遍历的过程中，我们其实做了很多“多余”的事情。
拿第三个索引位上这个 75 来说，我们在定位比 75 高的第一个温度的过程中，就路过了 71、69、72 这三个温度，其中，72 正是 71 对应的目标温度，可我们却像没看见它一样、啥也没干。只有等最外层遍历走到 71 时，我们才又重复了一遍刚刚走过的路、确认了 71 和 72 之间的关系——像这种不必要的重复，我们要想办法把它干掉。
栈结构可以帮我们避免重复操作。
避免重复操作的秘诀就是及时地将不必要的数据出栈，避免它对我们后续的遍历产生干扰。
拿这道题来说，我们的思路就是：尝试去维持一个递减栈。
当遍历过的温度，维持的是一个单调递减的态势时，我们就对这些温度的索引下标执行入栈操作；只要出现了一个数字，它打破了这种单调递减的趋势，也就是说它比前一个温度值高，这时我们就对前后两个温度的索引下标求差，得出前一个温度距离第一次升温的目标差值。这么说可能有点抽象，我们用一张动图来理解一下这个过程（这个过程实际有将近一分钟那么长，贴上来之后我发现完全加载不出来，这里呈现的是截止到第一个元素出栈的片段，完整的视频我这边上传到了小破站）：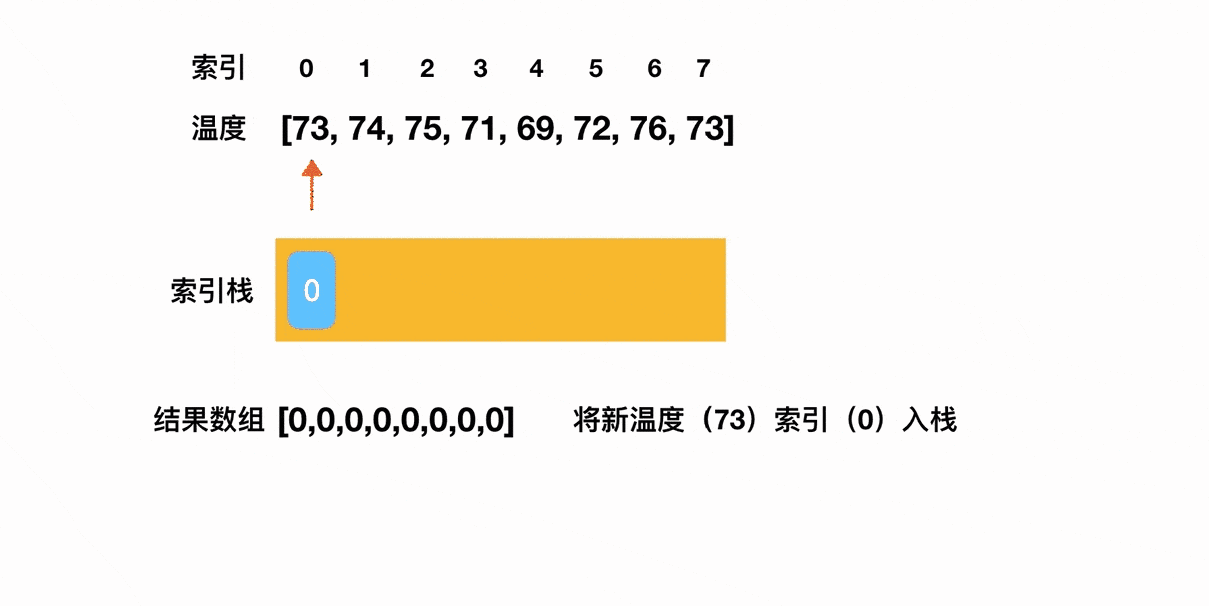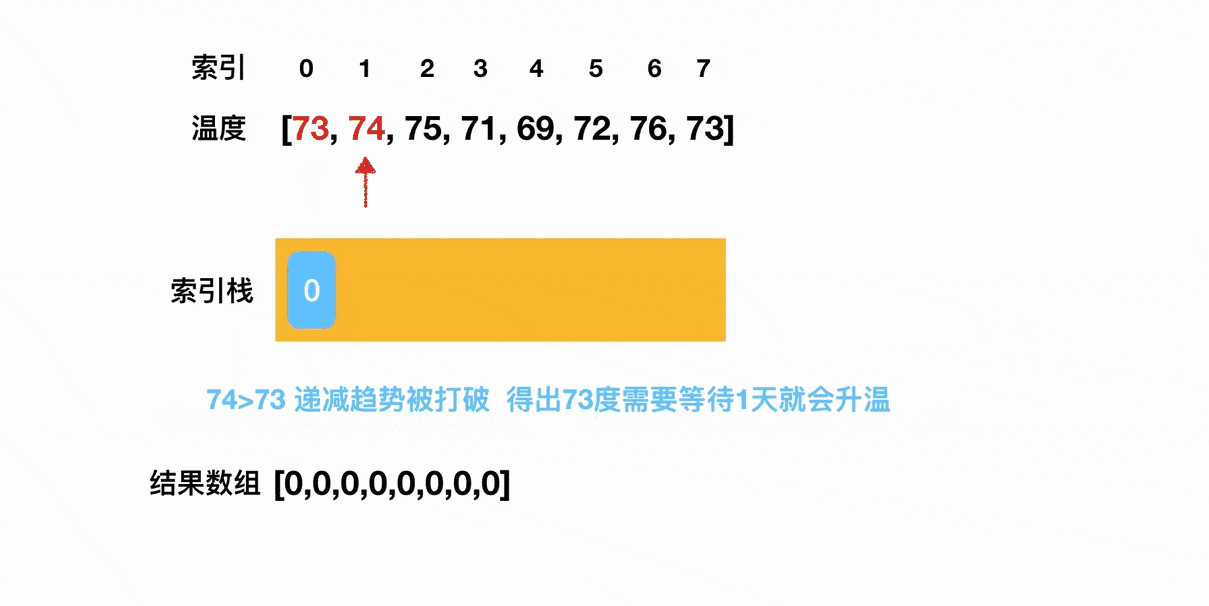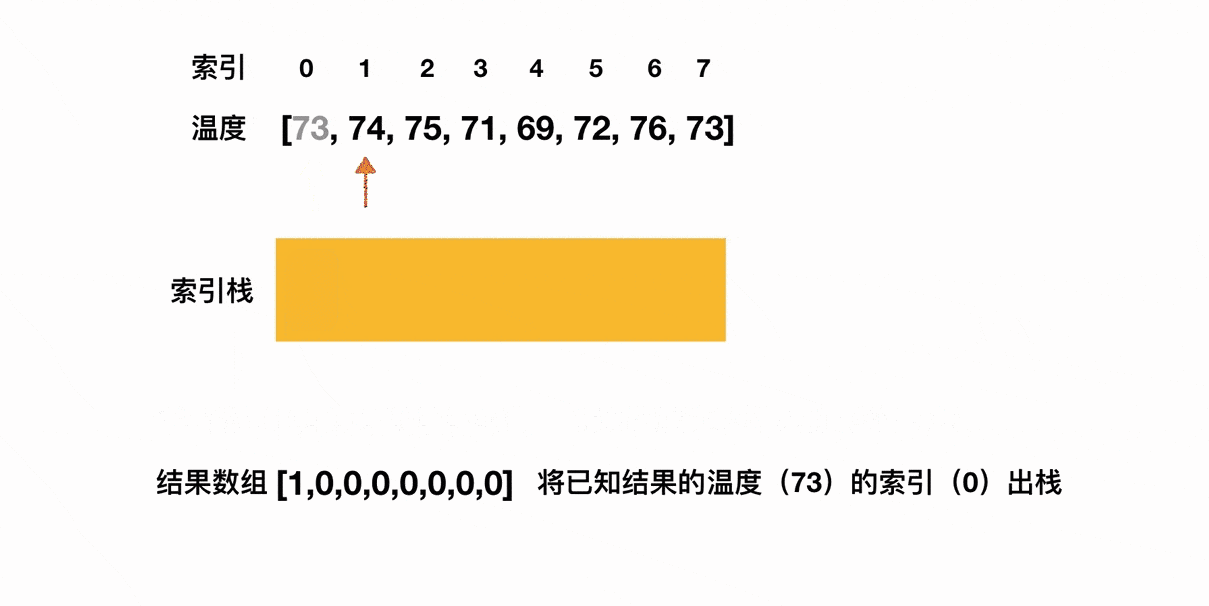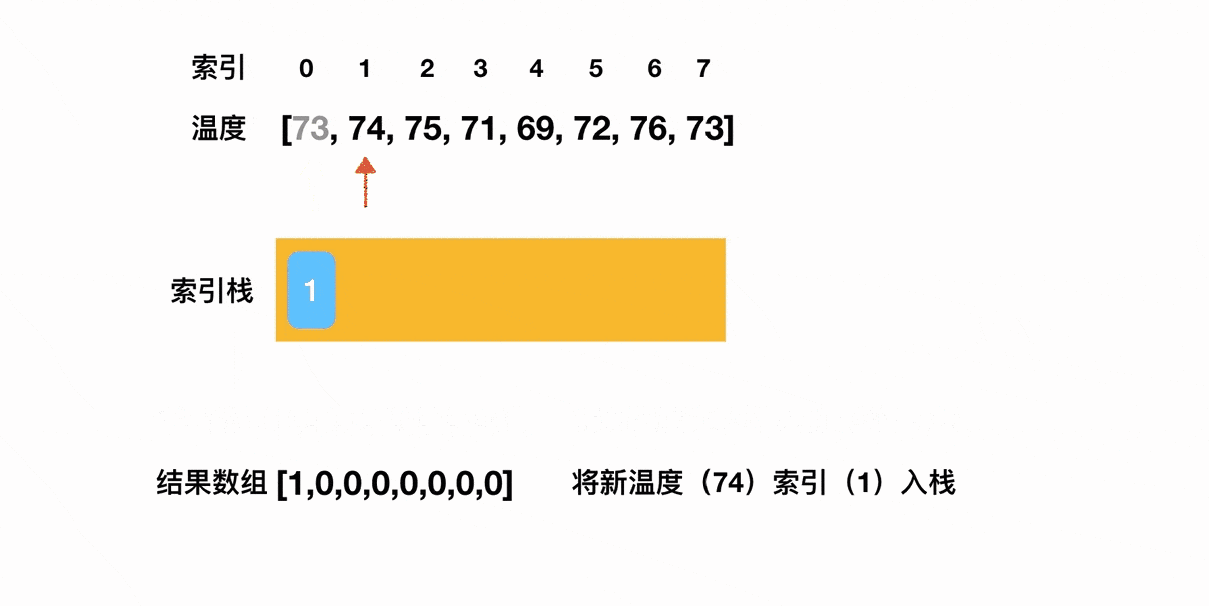
12 | 栈与队列怎么玩（上） - 图1

在这个过程中，我们仅对每一个温度执行最多一次入栈操作、一次出栈操作，整个数组只会被遍历一次，因此时间复杂度就是O(n)。相对于两次遍历带来的 O(n^2)的开销来看，栈结构真是帮了咱们大忙了。

编码实现

  1. /**
  2.  * @param {number[]} T
  3.  * @return {number[]}
  4.  */
  5. // 入参是温度数组
  6. const dailyTemperatures = function(T) {
  7.     const len = T.length // 缓存数组的长度 
  8.     const stack = [] // 初始化一个栈   
  9.     const res = (new Array(len)).fill(0) //  初始化结果数组，注意数组定长，占位为0
  10.     for(let i=0;i<len;i++) {
  11.       // 若栈不为0，且存在打破递减趋势的温度值
  12.       while(stack.length && T[i] > T[stack[stack.length-1]]) {
  13.         // 将栈顶温度值对应的索引出栈
  14.         const top = stack.pop()  
  15.         // 计算 当前栈顶温度值与第一个高于它的温度值 的索引差值
  16.         res[top] = i - top 
  17.       }
  18.       // 注意栈里存的不是温度值，而是索引值，这是为了后面方便计算
  19.       stack.push(i)
  20.     }
  21.     // 返回结果数组
  22.     return res 
  23. };

栈的设计——“最小栈”问题

题目描述：设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。 push(x) —— 将元素 x 推入栈中。

pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); —> 返回 -3.
minStack.pop();
minStack.top(); —> 返回 0.
minStack.getMin(); —> 返回 -2.

思路分析

这道题并不难，但是综合性很强，整个题做下来能够相对全面地考察到候选人对栈结构、栈操作的理解和掌握，是不少一面/少数二面面试官的心头好。
其中前三个操作：push、pop 和 top，我们在数据结构快速上手环节已经给大家讲过了，这里不多赘述。需要展开讲的是 getMin 这个接口，这个接口有时候会直接单独拎出来作为一道题来考察，需要大家对它的实现思路有一个真正扎实的掌握。
getMin 要做的事情，是从一个栈里找出其中最小的数字。我们仍然是抛砖引玉，先说一个大部分人都能想到的思路：
初始化一个最小值变量，它的初始值可以设一个非常大的数（比如 Infinity），然后开始遍历整个栈。在遍历的过程中，如果遇到了更小的值，就把最小值变量更新为这个更小的值。这样遍历结束后，我们就能拿到栈中的最小值了。
这个过程中，我们对栈进行了一次遍历，时间复杂度无疑是 O(n)。
按照这个思路，整个栈的设计我们可以这样写：

编码实现1

  1. /**
  2.  * 初始化你的栈结构
  3.  */
  4. const MinStack = function() {
  5.   this.stack = []
  6. };
  7. /** 
  8.  * @param {number} x
  9.  * @return {void}
  10.  */
  11. // 栈的入栈操作，其实就是数组的 push 方法
  12. MinStack.prototype.push = function(x) {
  13.   this.stack.push(x)
  14. };
  15. /**
  16.  * @return {void}
  17.  */
  18. // 栈的入栈操作，其实就是数组的 pop 方法
  19. MinStack.prototype.pop = function() {
  20.   this.stack.pop()
  21. };
  22. /**
  23.  * @return {number}
  24.  */
  25. // 取栈顶元素，咱们教过的哈，这里我本能地给它一个边界条件判断（其实不给也能通过，但是多做不错哈）
  26. MinStack.prototype.top = function() {
  27.   if(!this.stack || !this.stack.length) {
  28.       return 
  29.   }
  30.   return this.stack[this.stack.length - 1]
  31. };
  32. /**
  33.  * @return {number}
  34.  */
  35. // 按照一次遍历的思路取最小值
  36. MinStack.prototype.getMin = function() {
  37.     let minValue = Infinity  
  38.     const  { stack } = this
  39.     for(let i=0; i<stack.length;i++) {
  40.         if(stack[i] < minValue) {
  41.             minValue = stack[i]
  42.         }
  43.     }
  44.     return minValue
  45. };

这样写，用例也能跑通，但是不够酷。如果你在面试时这样做了，面试官有99%的可能性会追问你这句：
“这道题有没有时间效率更高的做法？”
人家都这样问了，咱当然要说“有”。然后，面试官就会搬个小板凳，坐你旁边看你如何妙手回春，变 O(n) 为 O(1)。
时间效率的提升，从来都不是白嫖，它意味着我们要付出更多的空间占用作为代价。在这道题里，如果继续沿着栈的思路往下走，我们可以考虑再搞个栈（stack2）出来作为辅助，让这个栈去容纳当前的最小值。
如何确保 stack2 能够确切地给我们提供最小值？ 这里我们需要实现的是一个从栈底到栈顶呈递减趋势的栈（敲黑板！递减栈出现第二次了哈）：

  • 取最小值：由于整个栈从栈底到栈顶递减，因此栈顶元素就是最小元素。
  • 若有新元素入栈：判断是不是比栈顶元素还要小，否则不准进入 stack2。
  • 若有元素出栈：判断是不是和栈顶元素相等，如果是的话，stack2 也要出栈。

按照这个思路，我们可以有以下编码：

编码实现2

  1. const MinStack = function() {
  2.     this.stack = [];
  3.     // 定义辅助栈
  4.     this.stack2 = [];
  5. };
  6. /** 
  7.  * @param {number} x
  8.  * @return {void}
  9.  */
  10. MinStack.prototype.push = function(x) {
  11.     this.stack.push(x);
  12.     // 若入栈的值小于当前最小值，则推入辅助栈栈顶
  13.     if(this.stack2.length == 0 || this.stack2[this.stack2.length-1] >= x){
  14.         this.stack2.push(x);
  15.     }
  16. };
  17. /**
  18.  * @return {void}
  19.  */
  20. MinStack.prototype.pop = function() {
  21.     // 若出栈的值和当前最小值相等，那么辅助栈也要对栈顶元素进行出栈，确保最小值的有效性
  22.     if(this.stack.pop() == this.stack2[this.stack2.length-1]){
  23.         this.stack2.pop();
  24.     }
  25. };
  26. /**
  27.  * @return {number}
  28.  */
  29. MinStack.prototype.top = function() {
  30.     return this.stack[this.stack.length-1];
  31. };
  32. /**
  33.  * @return {number}
  34.  */
  35. MinStack.prototype.getMin = function() {
  36.     // 辅助栈的栈顶，存的就是目标中的最小值
  37.     return this.stack2[this.stack2.length-1];
  38. };