二叉搜索树是二叉树的特例，平衡二叉树则是二叉搜索树的特例。

什么是平衡二叉树

在上一节的末尾，我们已经通过一道真题和平衡二叉树打过交道。正如题目中所说，平衡二叉树（又称 AVL Tree）指的是任意结点的左右子树高度差绝对值都不大于1的二叉搜索树。

为什么要有平衡二叉树

平衡二叉树的出现，是为了降低二叉搜索树的查找时间复杂度。
大家知道，对于同样一个遍历序列，二叉搜索树的造型可以有很多种。拿 [1,2,3,4,5]这个中序遍历序列来说，基于它可以构造出的二叉搜索树就包括以下两种造型：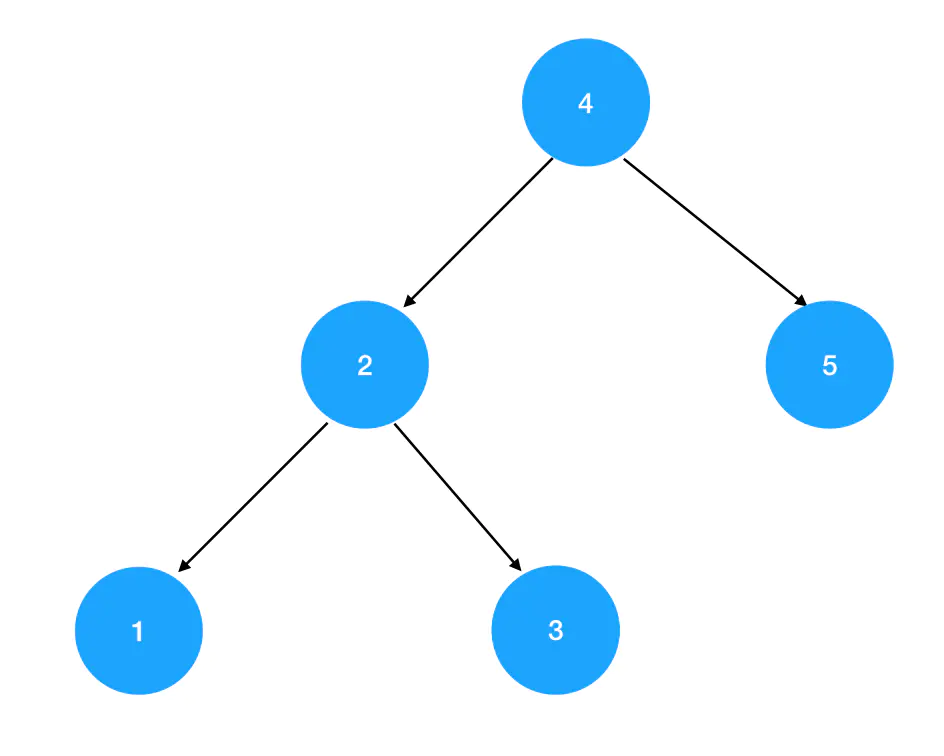
18 | 特殊的二叉树——平衡二叉树专题 - 图1
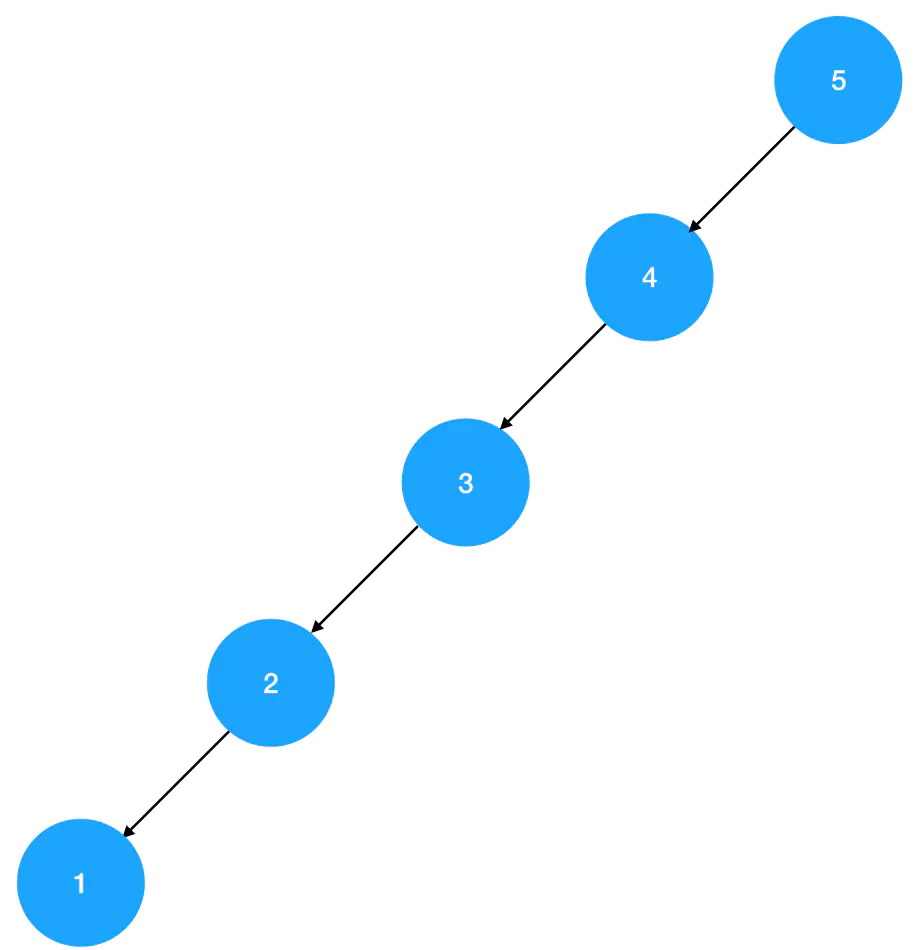18 | 特殊的二叉树——平衡二叉树专题 - 图2 结合平衡二叉树的定义，我们可以看出，第一棵二叉树是平衡二叉树，第二棵二叉树是普通的二叉搜索树。
现在，如果要你基于上一节学过的二叉搜索树查找算法，在图上两棵树上分别找出值为1的结点，问你各需要查找几次？在1号二叉树中，包括根结点在内，只需要查找3次；而在2号二叉树中，包括根结点在内，一共需要查找5次。
我们发现，在这个例子里，对于同一个遍历序列来说，平衡二叉树比非平衡二叉树（图上的结构可以称为链式二叉树）的查找效率更高。这是为什么呢？
大家可以仔细想想，为什么科学家们会无中生有，给二叉树的左右子树和根结点之间强加上排序关系作为约束，进而创造出二叉搜索树这种东西呢？难道只是为了装x吗？当然不是啦。二叉搜索树的妙处就在于它把“二分”这种思想以数据结构的形式表达了出来。在一个构造合理的二叉搜索树里，我们可以通过对比当前结点和目标值之间的大小关系，缩小下一步的搜索范围（比如只搜索左子树或者只搜索右子树），进而规避掉不必要的查找步骤，降低搜索过程的时间复杂度。但是如果一个二叉搜索树严重不平衡，比如说上面这棵链式搜索树：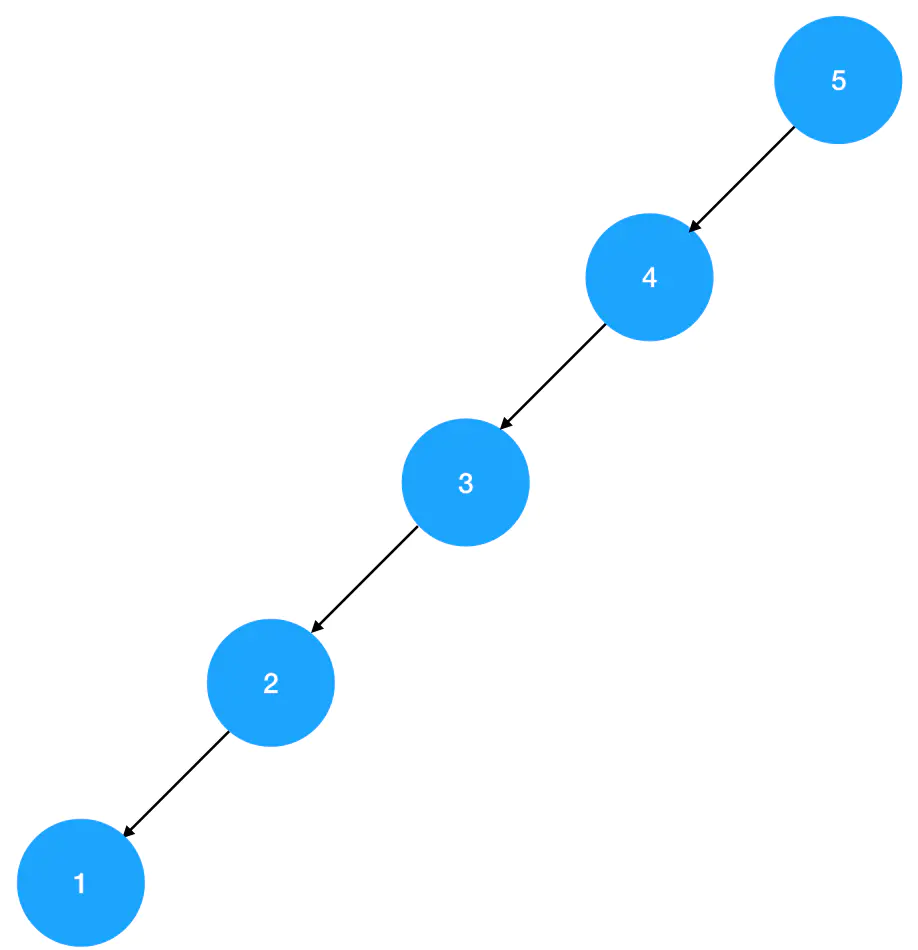
18 | 特殊的二叉树——平衡二叉树专题 - 图3
每一个结点的右子树都是空的，这样的结构非常不合理，它会带来高达O(N)的时间复杂度。而平衡二叉树由于利用了二分思想，查找操作的时间复杂度仅为 O(logN)。因此，为了保证二叉搜索树能够确实为查找操作带来效率上的提升，我们有必要在构造二叉搜索树的过程中维持其平衡度，这就是平衡二叉树的来由。

命题思路解读

平衡二叉树和二叉搜索树一样，都被归类为“特殊”的二叉树。对于这样的数据结构来说，其“特殊”之处也正是其考点所在，因此真题往往稳定地分布在以下两个方向：

  • 对特性的考察（本节以平衡二叉树的判定为例）
  • 对操作的考察（本节以平衡二叉树的构造为例）

    平衡二叉树的判定

    题目描述：给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为： 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

  1. 3
  2.    / \
  3.   9  20
  4.     /  \
  5.    15   7

返回 true 。 示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

  1. 1
  2.       / \
  3.      2   2
  4.     / \
  5.    3   3
  6.   / \
  7.  4   4

返回 false 。

思路分析

来，我们复习一遍平衡二叉树的定义：

平衡二叉树是任意结点的左右子树高度差绝对值都不大于1的二叉搜索树。

抓住其中的三个关键字：

  1. 任意结点
  2. 左右子树高度差绝对值都不大于1
  3. 二叉搜索树

注意，结合题意，上面3个关键字中的3对这道题来说是不适用的，因此我们不必对二叉搜索树的性质进行校验。现在只看 1 和 2，先给自己一分钟思考一下——你可以提取出什么线索？
“任意结点”什么意思？每一个结点都需要符合某个条件，也就是说每一个结点在被遍历到的时候都需要重复某个校验流程，对不对？
哎，我刚刚是不是说了什么不得了的动词了？啊，是重复！是tmd的重复啊！！！来，学到了第18节，为了向我证明你没有跳读，请大声喊出下面这两个字：
递归！
没错，“任意结点”这四个字，就是在暗示你用递归。而“左右子树高度差绝对值都不大于1”这个校验规则，就是递归式。
啊，真让人激动呢，解决这道题的思路竟然已经慢慢浮现出来了，那就是：从下往上递归遍历树中的每一个结点，计算其左右子树的高度并进行对比，只要有一个高度差的绝对值大于1，那么整棵树都会被判为不平衡。

编码实现

  1. const isBalanced = function(root) {
  2.   // 立一个flag，只要有一个高度差绝对值大于1，这个flag就会被置为false
  3.   let flag = true
  4.   // 定义递归逻辑
  5.   function dfs(root) {
  6.       // 如果是空树，高度记为0；如果flag已经false了，那么就没必要往下走了，直接return
  7.       if(!root || !flag) {
  8.           return 0 
  9.       }
  10.       // 计算左子树的高度
  11.       const left = dfs(root.left)  
  12.       // 计算右子树的高度
  13.       const right = dfs(root.right)  
  14.       // 如果左右子树的高度差绝对值大于1，flag就破功了
  15.       if(Math.abs(left-right) > 1) {
  16.           flag = false
  17.           // 后面再发生什么已经不重要了，返回一个不影响回溯计算的值
  18.           return 0
  19.       }
  20.       // 返回当前子树的高度
  21.       return Math.max(left, right) + 1
  22.   }
  24.   // 递归入口
  25.   dfs(root) 
  26.   // 返回flag的值
  27.   return flag
  28. };

平衡二叉树的构造

题目描述：给你一棵二叉搜索树，请你返回一棵平衡后的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。

如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是平衡的。
如果有多种构造方法，请你返回任意一种。

示例：

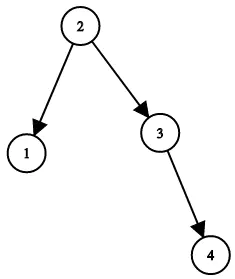
18 | 特殊的二叉树——平衡二叉树专题 - 图4 18 | 特殊的二叉树——平衡二叉树专题 - 图5

输入：root = [1,null,2,null,3,null,4,null,null]

输出：[2,1,3,null,null,null,4]
解释：这不是唯一的正确答案，[3,1,4,null,2,null,null] 也是一个可行的构造方案。

提示：

树节点的数目在 1 到 10^4 之间。 树节点的值互不相同，且在 1 到 10^5 之间。

思路分析

这道题乍一看有点唬人，可能会直接干懵一部分同学。不过不用慌——题目再新，套路依旧。只要你对核心考点把握得足够扎实，它就难不倒你。
我们来分析一下这道题的核心诉求：要求我们构造一棵平衡的二叉搜索树。先抛开题干中各种前置条件不谈，单看这个输出结果，你会不会有一种似曾相识的感觉呢？没错，在上一节的最后一道真题中，我们也构造过这样的一棵二叉树。
那么这两道题之间会不会有什么微妙的联系呢？答案是会，不然，笔者也不会把它们放得这么近（疯狂暗示）。两道题之间唯一的差别在于输入：在我们已经做过的那道题中，输入参数是一个有序数组；而这道题中，输入参数是一个二叉搜索树。
唔，再想想！上一节那道题里的“有序数组”，和眼前这道题里的“二叉搜索树”之间，会不会有什么妙不可言的关系呢？
别忘了，二叉搜索树的中序遍历序列是有序的！所谓有序数组，完全可以理解为二叉搜索树的中序遍历序列啊，对不对？现在树都给到咱们手里了，求它的中序遍历序列是不是非常 easy？如果能把中序遍历序列求出来，这道题是不是就跟之前做过那道是一模一样的解法了？
没错，这道题的解题思路正是：

  1. 中序遍历求出有序数组

  2. 逐个将二分出来的数组子序列“提”起来变成二叉搜索树

    编码实现

    1. /**
    2. * @param {TreeNode} root
    3. * @return {TreeNode}
    4. */
    5. const balanceBST = function(root) {
    6.  // 初始化中序遍历序列数组
    7.  const nums = []
    8.  // 定义中序遍历二叉树，得到有序数组
    9.  function inorder(root) {
    10.      if(!root) {
    11.          return 
    12.      }
    13.      inorder(root.left)  
    14.      nums.push(root.val)  
    15.      inorder(root.right)
    16.  }
    18.  // 这坨代码的逻辑和上一节最后一题的代码一模一样
    19.  function buildAVL(low, high) {
    20.      // 若 low > high，则越界，说明当前索引范围对应的子树已经构建完毕
    21.      if(low>high) {
    22.          return null
    23.      }
    24.      // 取数组的中间值作为根结点值
    25.      const mid = Math.floor(low + (high -low)/2)
    26.      // 创造当前树的根结点
    27.      const cur = new TreeNode(nums[mid])  
    28.      // 构建左子树
    29.      cur.left = buildAVL(low, mid-1) 
    30.      // 构建右子树
    31.      cur.right = buildAVL(mid+1, high)  
    32.      // 返回当前树的根结点 
    33.      return cur
    34.  }
    35.  // 调用中序遍历方法，求出 nums
    36.  inorder(root)
    37.  // 基于 nums，构造平衡二叉树
    38.  return buildAVL(0, nums.length-1)
    39. };