单细胞中的流形（二）：UMAP与tSNE的区别

UMAP(Uniform Manifold Approximation and Projection) 是一种类似tSNE的高维数据降维算法，由加拿大Tutte数学和计算研究所的Leland McInnes开发[1]。UMAP相对于tSNE有以下两个主要优势：
1. 能反映全局结构；
2. 计算大样本数据时，运行速度较快，占用内存较少。

两个例子的比较
先举两个例子直观感受UMAP和tSNE的区别。下图1展示小鼠胚胎E10.5-E17.5 双潜能成肝细胞分化为肝实质细胞和肝内胆管细胞的过程，数据来源于 2017 年北大徐成冉课题组发表在《Hepatology》杂志上的文章数据GSE90047[2]。UMAP更能反映发育时序上的连续性。而tSNE细胞类型的区分度更好。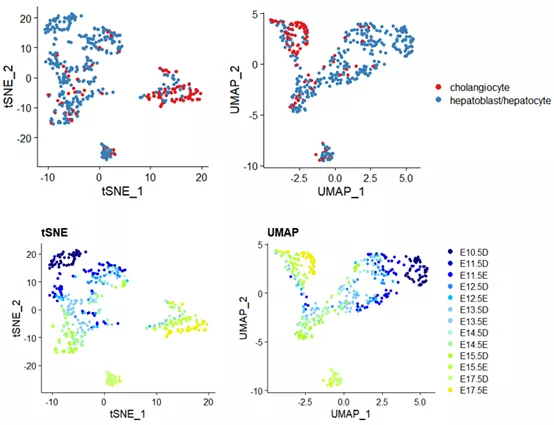

图1. 小鼠胚胎肝脏发育

图2是UMAP作者和合作方2019年发表在《Nature Biotechnology》上关于UMAP在单细胞数据上应用的文章截图，细胞数超过30万个[3]。可以直观看出，CD8+T细胞（绿色点）在UMAP中很好的聚在一个区域，而在tSNE中分散为两大块。说明在大数据的例子中，UMAP相对于tSNE能更好的反映数据的全局结构。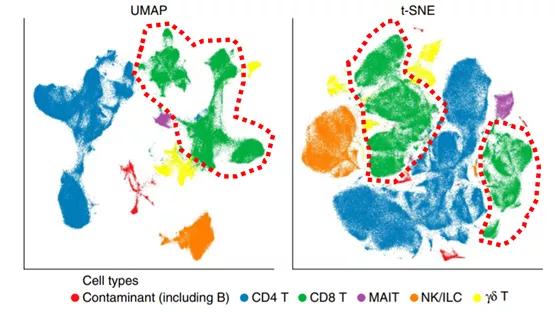

图2. 免疫细胞

UMAP为何能有如此优势？

UMAP的算法框架和tSNE的框架相似。关于tSNE的算法原理，可以回顾一下本公众号的上一期文章：单细胞中的流形（一）：tSNE中的perplexity。

先总结UMAP和tSNE在算法上的主要区别：
1. 高维数据和低维数据转换距离分布时，UMAP没有进行标准化；（省时）
2. 计算σ时，UMAP用邻近个数代替tSNE的perplexity；（省时）
3. UMAP不直接用t分布拟合低维数据，添加参数动态调整，但是接近t分布；
4. UMAP的损失函数用Cross-Entropy(CE)代替tSNE的KL散度；（全局）
5. UMAP用随机梯度下降（SGD）代替tSNE的梯度下降法（GD）。（省时省内存）

UMAP的重要参数：

1. number of nerghbor. 邻近个数，大小会影响σ值。作用与tSNE中的perplexity相似。邻近个数设置越大，流形特征范围越大，细胞分群更加集中。
   

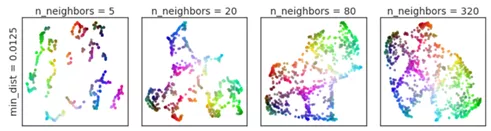
2. Minimum distance. 最小距离，拟合低维距离分布的公式时需要用到的参数。最小距离越小，点的分布越松散。
   

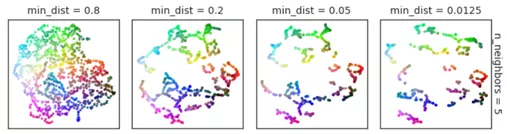
下面介绍UMAP的算法原理。有些部分参考了瑞典隆德大学Nikolay Oskolkov的文章。他写的单细胞相关的算法都很好，值得一看[4]。

UMAP算法原理

高维数据处理。UMAP高维数据距离转化公式跟tSNE很像，但是有两个主要区别：

• 距离不一定是欧式距离
• 所有点与i点的距离加上与i点最近的点的距离ρ。ρ参数的添加能更好的反映高维数据的局部流形。

UMAP不对标转化后的距离标准化。同时，后面的低维数据也没有标准化。

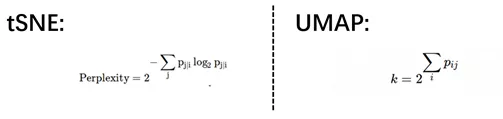
σ计算方式。UMAP用i点与其他点距离的总和代替tSNE的perplexity中的香农熵。k也是UMAP输入参数numberof neighbor.

距离矩阵的对称化。暂时没看出这两种对称化方法的效果差异。

低维数据距离分布拟合。UMAP的分布模型比tSNE的t分布多了a，b两个参数。当a和b都等于1时，才是t分布。a和b由输入参数minimum distance确定。

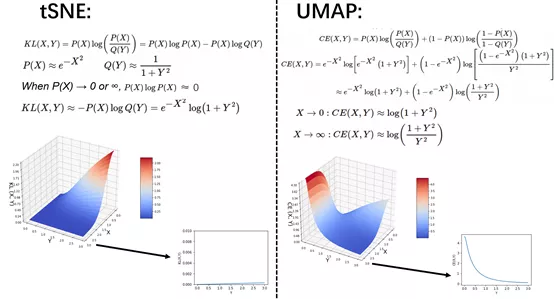
损失函数。低维距离分布向高维距离分布拟合，需要损失函数来衡量。通过梯度优化，得到损失函数值最小的低维距离分布，也就是2维或3维的可视化图。当高维数据细胞间的距离X较大时，随着低维距离Y变小，tSNE的损失函数值变化不大。换句话说，X较大时，Y可能取较小的值，失真。所以tSNE只保留局部结构，全局不太准。而UMAP在高维距离X较大时，还保持着损失函数的有效性，低维距离Y取值越小，损失函数值越大，惩罚越大。所以UMAP可以保留全局结构。

梯度优化用随机梯度下降法（Stochastic Gradient Descent）代替梯度下降法（Gradient Descent）。

tSNE梯度优化过程：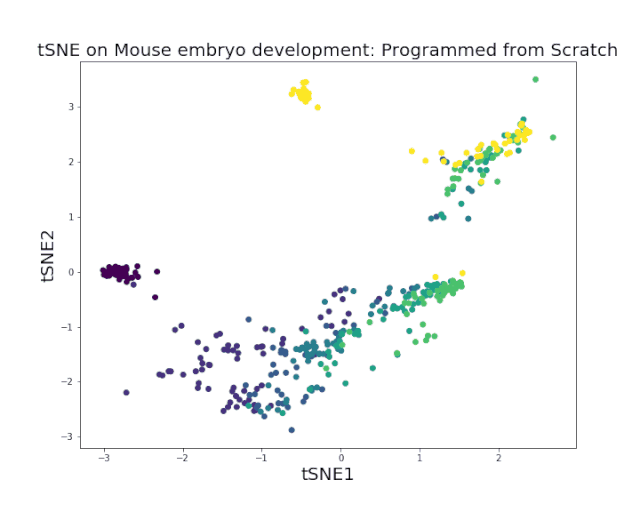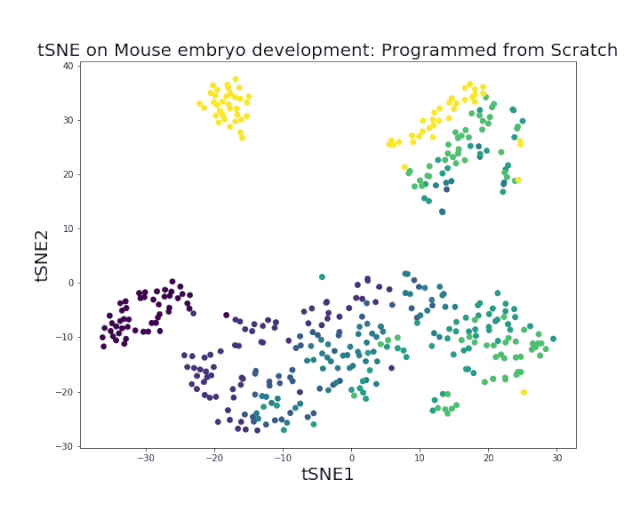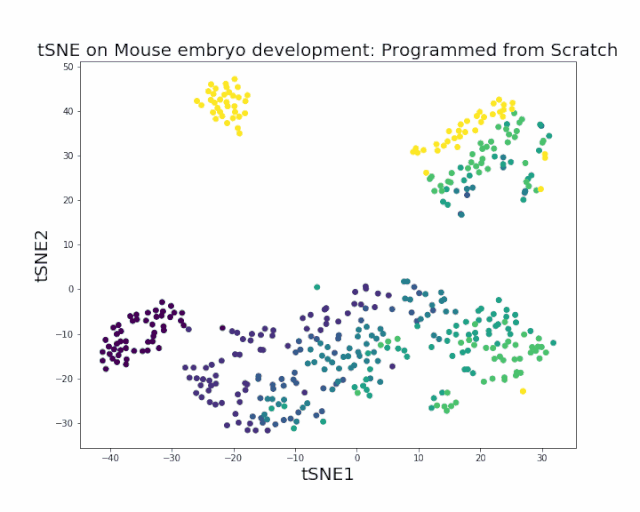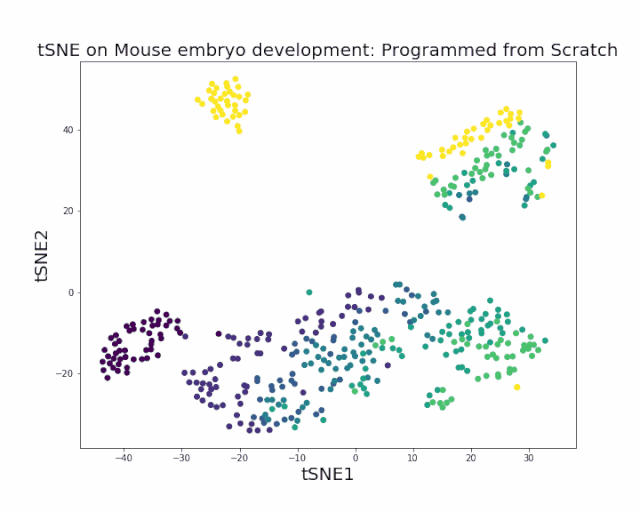

UMAP梯度优化过程:

数据与代码实现：
https://github.com/Zhihao-Huang/SingleCellOmics/tree/master/UMAP_tSNE

UMAP的不足与改进思路

1. 维度不像PCA的主成分或者非负矩阵分解的因子可解释。只能用于可视化。
   2. 样本较小时（n < 500），可能效果不好，需要慎重选择参数。
   3. 局部的聚类效果有时没有tSNE的效果好（图1），相似的细胞分群靠得太近，区分度不高，如果数据质量较差，会影响可视化效果。这也是目前仍然有不少文章用tSNE的原因之一。UMAP的低维数据转换模型y= 1 / (1 + ax^(2b))仍然有改进的地方。
   4. 比tSNE更能反映全局结构，但不代表UMAP是最好的全局结构展示方法。

下期预告：单细胞中的流形（三）：diffusion maps

参考链接：
[1] McInnes L, Healy J, Melville J.Umap: Uniform manifold approximation and projection for dimension reduction[J].arXiv preprint arXiv:1802.03426, 2018.
[2] Yang L, Wang W H, Qiu W L, et al. Asingle‐celltranscriptomic analysis reveals precise pathways and regulatory mechanismsunderlying hepatoblast differentiation[J]. Hepatology, 2017, 66(5): 1387-1401.
[3] Becht E, McInnes L, Healy J, et al.Dimensionality reduction for visualizing single-cell data using UMAP[J]. Naturebiotechnology, 2019, 37(1): 38.
[4] https://towardsdatascience.com/tagged/stats-ml-life-sciences