由于单细胞转录组独特的数据结构，各式各样的算法与软件前仆后继，只为一层层地揭开单细胞的神秘面纱。从单细胞水平探索生命活动的过程，可以更好解析疾病的发生机制，推动基础医学转化。

之前介绍了tSNE和UMAP如何展示单细胞中的流形，这次介绍马尔科夫矩阵（Markov matrix）在各种单细胞分析算法中的应用，然后做一下总结。主要分以下四个部分：

  1. 马尔科夫链和马尔科夫矩阵；
  2. diffusion maps降维原理[1]，R基础代码简单实现，以及在时序分析中的应用；
  3. MAGIC对单细胞数据的插补原理；
  4. PHATE在单细细胞时序分析中的应用。

以上三个工具Diffusion maps/MAGIC/PHATE的基本算法原理都用到了马尔科夫矩阵。我们先从马尔科夫矩阵开始，然后看看大佬们是怎么利用这个算法，东拼西凑发Nature/NBT/Cell。

马尔科夫链和马尔科夫矩阵

马尔科夫链可以应用于城市人口流动和基因遗传分析。我们以人口流动为例解释。假设三个城市a/b/c的人口初始分布w是0.2，0.7，0.1，一个月后迁徙到其他城市的概率是矩阵P，那么一个月后的人口分布是wP，其中转移概率矩阵P即是马尔科夫矩阵，主要特征是所有元素大于等于0，每一行之和等于1。
单细胞中的流形（三）：时序分析中的马尔科夫链 - 图1

Diffusion maps降维原理以及在时序分析中的应用

相对于tSNE和UMAP，diffusion maps可视化效果更能直接反映细胞状态持续变化的位置关系。下图的diffusion maps用R包destiny分析。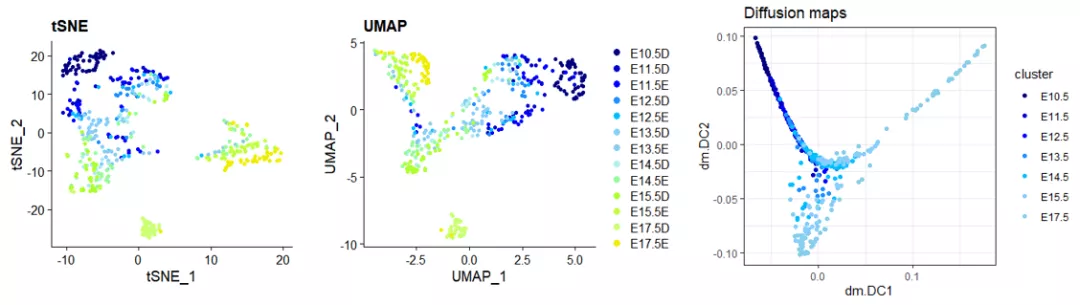
单细胞中的流形（三）：时序分析中的马尔科夫链 - 图2
Diffusion maps降维单细胞数据，首先需要用表达矩阵通过高斯核函数计算得到细胞与细胞之间的距离方阵A，这一步和tSNE的高维处理一样。然后方阵除以每一行之和，得到马尔科夫矩阵。接下来是diffusion maps的关键一步，马尔科夫矩阵相乘，在几何空间上表现为细胞的随机游走。走的步数越多，度量的路径越多，最后趋于稳定。因为diffusion maps以diffuse distance作为距离的衡量，很少受到特殊噪杂信息的影响。游走扩散t步之后，P^t的特征值和特征向量的相乘得到diffusion maps可视化的2/3维。
单细胞中的流形（三）：时序分析中的马尔科夫链 - 图3
单细胞中的流形（三）：时序分析中的马尔科夫链 - 图4

在实际计算中P^t的特征值分解可以用D^-0.5A D^-0.5的特征值分解代替，其中A为高斯核距离方阵，D为A的行和的对角矩阵。
Diffusion maps代码实现：

  2. ##Transfer high dimensional distance toprobability
  3. ##load data
  4. mouse.data <-read.table("./mousedata/scRNA-seq_TPM_GSE90047.xls",header=T,row.names=1)
  5. mouse.celltypes <-read.table("./mousedata/XCR_paper_cell_anno_sub.txt",header =T,row.names = 1,stringsAsFactors = F,sep="\t")
  6. mouse.anno <-read.csv("./mousedata/mus_gene_anno.txt",sep='\t',row.names=1)
  7. mouse.anno <-mouse.anno[!duplicated(mouse.anno$Symbol),]
  8. commonID <-intersect(rownames(mouse.data),mouse.anno$ID)
  9. mouse.anno <- mouse.anno[commonID,]
  10. mouse.data <- mouse.data[commonID,]
  11. rownames(mouse.data) <-mouse.anno$Symbol
  13. ##min cell 5 and min features 1000
  14. mouse.data <-mouse.data[apply(mouse.data,1,function(x) sum(x>0)>=5),apply(mouse.data,2,function(x)sum(x>0)>=1000)]
  16. ##log normalization
  17. data_nor <-apply(mouse.data,2,function(x) log(x/sum(x)*10000+1))
  18. ##using the top 50 PCs as features
  19. data_pca50 <- prcomp(data_nor,rank. =50)
  20. data_pca50$rotation[1:5,1:5]
  21. distmat <- dist(data_pca50$rotation)
  23. #from seurat
  24. distmat <-dist(mouse@reductions$pca@cell.embeddings)
  25. ##calculate euclidean distance
  26. distmat <- dist(t(data_nor))
  27. distmat <- as.matrix(distmat)
  29. ##Transfer high dimensional distance toprobability using Gaussian kernel
  30. #In order to simplify this example, we usea stable sigma 'SD' here.
  31. SD <- 10
  32. probmat <- exp(-(distmat^2)/(2*(SD^2)))
  34. ##Create symmetric markovian  Matrix
  35. d_rot <- Diagonal(x =rowSums(probmat)^-.5)
  36. mrk <- d_rot %*% probmat %*% d_rot
  37. ei <- eigen(mrk)
  38. #ei$vectors <- ei$vectors %*% d_rot
  39. DC1 <- ei$values[2] * ei$vectors[,2]
  40. DC2 <- ei$values[3] * ei$vectors[,3]
  41. color_palette <-c('#000080','#0000CD','#0000FF','#1E90FF','#00BFFF','#87CEFA','#87CEEB',
  42.                   '#AFEEEE','#98FB98','#ADFF2F','#C0FF3E','#CAFF70','#EEEE00')
  43. data <-data.frame(DC1,DC2,stringsAsFactors = F)
  44. stage <- cluster[names(cluster) %in%colnames(mouse.data)]
  45. ggplot(data,aes(DC1,DC2,color= stage)) +geom_point() + theme_bw()+
  46.  scale_color_manual(values = color_palette)

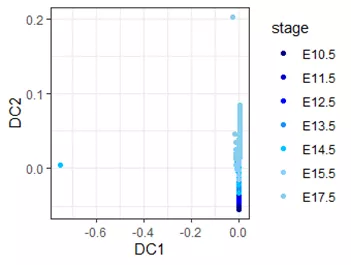
单细胞中的流形（三）：时序分析中的马尔科夫链 - 图5
由于sigma不做计算，固定为10，图有点难看，但趋势是有的。

MAGIC对单细胞数据的插补原理

MAGIC是一个处理dropout的单细胞数据插补工具，2018年发表在Cell杂志上[2]。这个工具的主要魔力是用马尔科夫矩阵乘以原始表达矩阵，得到的新矩阵考虑了其他细胞的表达量，以距离作为加权插补数据。
单细胞中的流形（三）：时序分析中的马尔科夫链 - 图6

PHATE在单细细胞时序分析中的应用

PHATE是类似于Diffusion maps的降维工具，2019年12月发表在Nature Biotechnology杂志上[3]，作者和MAGIC相同。
PHATE的高维数据转换和diffusion maps类似，高斯核函数中的sigma计算用量子力学中的冯诺依曼熵（von Neumann Entropy），其实和tSNE用的香农熵一样的公式，当量子态处于完全混合时，冯诺依曼熵退化为香农熵[4]。
PHATE主要创新点在于后面对马尔可夫矩阵做log标准化，然后计算欧式距离，最后用MDS降维展示。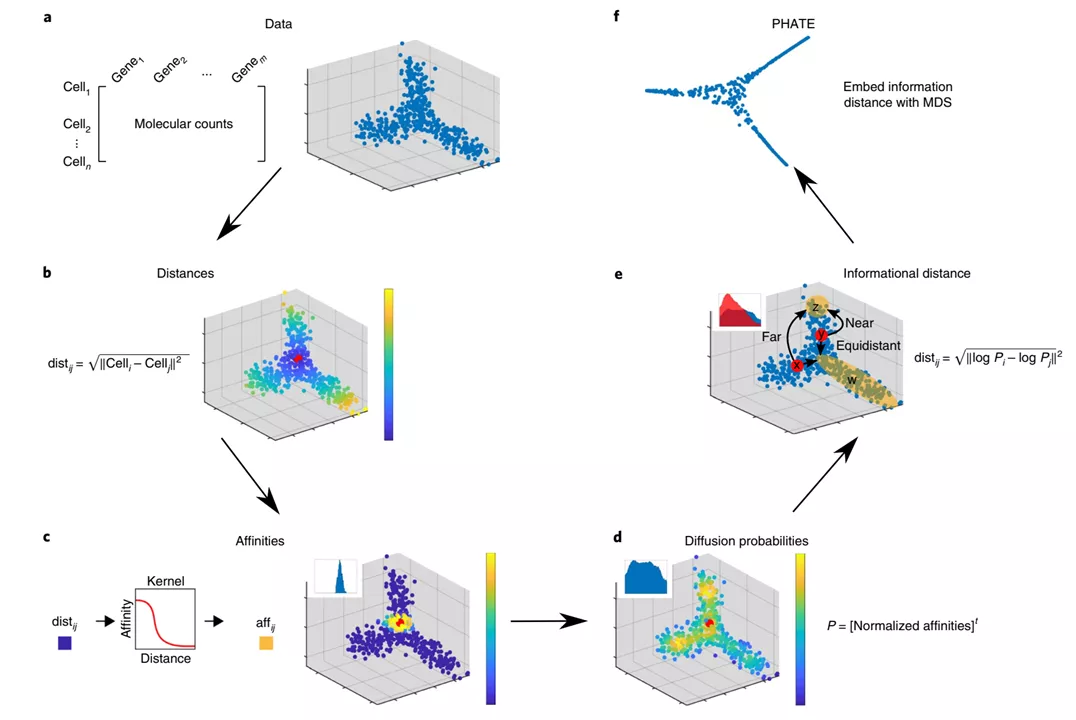
单细胞中的流形（三）：时序分析中的马尔科夫链 - 图7
最后总结一下单细胞流形专题中五个工具tSNE/UMAP/diffusion maps/MAGIC/PHATE的算法异同。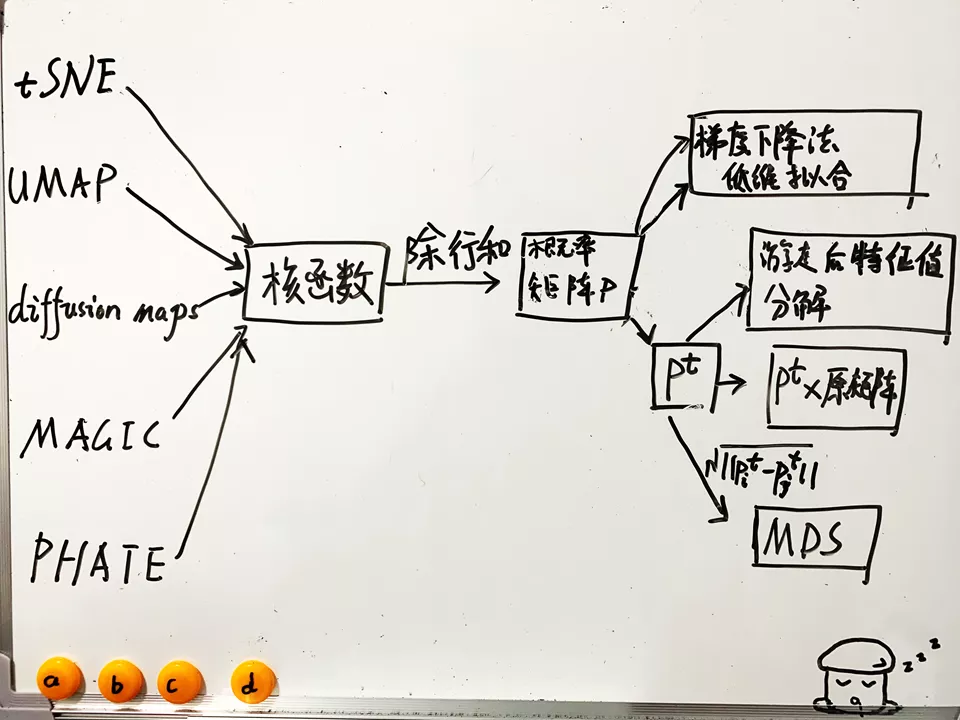
单细胞中的流形（三）：时序分析中的马尔科夫链 - 图8

单细胞组学下期预告：单细胞中的神经网络（一）：deconvolution

参考文献：
[1] De la Porte, J., et al. “Anintroduction to diffusion maps.” Proceedings of the 19th Symposium of thePattern Recognition Association of South Africa (PRASA 2008), Cape Town, SouthAfrica. 2008.
[2] Van Dijk, David, et al.”Recovering gene interactions from single-cell data using datadiffusion.” Cell 174.3 (2018): 716-729.
[3] Moon, van Dijk, Wang, Gigante et al.Visualizing Transitions and Structure for Biological Data Exploration. 2019.Nature Biotechnology.
[4] https://www.xzbu.com/9/view-7727366.htm