本文来自“单细胞组学”公众号 原文链接:https://mp.weixin.qq.com/s/uk5mKBYJm6LTc96WWPfWUg
最小二乘法(Least Squares, LS)不仅存在于数学课本中,也常见于科学研究的分析,比如梯度实验数据常用的拟合回归,机器学习算法之一支持向量机(SVM)也有所涉及。本期单细胞组学由孙炎同学介绍最小二乘法的基础解释,以及它的矩阵化运算。
向量相互正交
向量正交即向量相互垂直,满足x·y=0,或xTy=0,两个等式等价。
零向量0与任意向量正交。
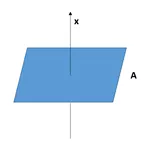
向量与向量空间正交
若向量x与向量空间A正交,则x与A中的任意一个向量y都正交(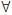 y ϵA,x·y=0)。
y ϵA,x·y=0)。
向量在向量上的正交投影
向量y在向量x上的正交投影为cx,满足x ·(y-cx)=0。
y的正交投影一般记为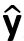 。
。
标量c的计算:由x ·(y-cx)=0,x·y-cx·x=0,c =x·y/x·x
,因此 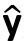 =(x·y/x·x) X。
=(x·y/x·x) X。
向量在向量空间上的正交投影
向量y在向量空间A上的正交投影为,满足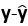 与向量空间A中的任意向量都正交。同时,对于空间A中的任意向量x,有||y-x||≥||
与向量空间A中的任意向量都正交。同时,对于空间A中的任意向量x,有||y-x||≥||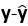 ||( || y-x ||表示向量y-x的长度 )。
||( || y-x ||表示向量y-x的长度 )。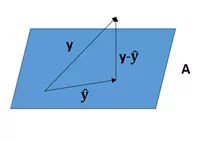
向量y在矩阵A的列空间(col A)上的正交投影的计算
1.已知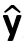 ϵ col A,故存在向量
ϵ col A,故存在向量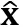 满足:
满足: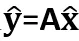
2. 向量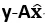 与向量空间col A正交,即向量
与向量空间col A正交,即向量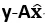 与矩阵A的每一列都正交,因此有a1T (
与矩阵A的每一列都正交,因此有a1T (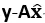 )=0,a2T (
)=0,a2T (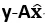 )=0,……,anT (
)=0,……,anT (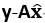 )=0(其中a1,a2,……,an为矩阵A的第1列,第2列,……,第n列),因此有
)=0(其中a1,a2,……,an为矩阵A的第1列,第2列,……,第n列),因此有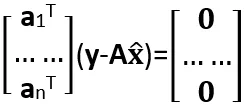 ,
,
即AT(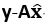 )=0,
)=0,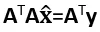
3. 根据方程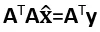 可解得
可解得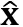 ,故y在矩阵A的列空间(col A)上的正交投影
,故y在矩阵A的列空间(col A)上的正交投影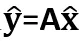 。
。
最小二乘问题
假设有一组成对的观测值x1,x2,……,xn; y1,y2,……,yn。现在需要用一条直线y=β0+β1x对x和y的关系进行拟合。
我们可以将这个方程写成Xβ=y,其中X=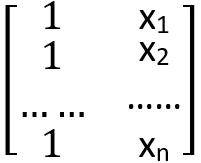 ,β=
,β=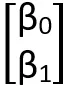 ,y=
,y=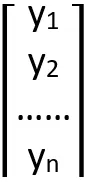 。
。
如果观测值x1,x2,……,xn; y1,y2,……,yn不在同一条直线上,那么满足方程Xβ=y的向量β是不存在的,但是我们可以求出一个 使得
使得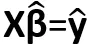 ,
, 是向量y在矩阵X的列空间(col X)的正交投影,这个就是方程的最小二乘解。向量的两个元素β0和β1满足y=β0+β1x是最小二乘直线。
是向量y在矩阵X的列空间(col X)的正交投影,这个就是方程的最小二乘解。向量的两个元素β0和β1满足y=β0+β1x是最小二乘直线。
证明:令y1’=β0+β1x1, y2’=β0+β1x2, ……, yn’=β0+β1xn,则向量
属于矩阵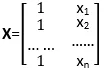
的列空间(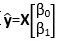 )。现在要调整参数β0和β1使得(y1-y1’)2 + (y2-y2’)2+ …… + (yn-yn’)2 最小,即
)。现在要调整参数β0和β1使得(y1-y1’)2 + (y2-y2’)2+ …… + (yn-yn’)2 最小,即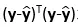 最小,即向量
最小,即向量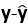 的长度最小。因为向量
的长度最小。因为向量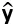 属于X的列空间(col X),则向量y-与col X正交时(
属于X的列空间(col X),则向量y-与col X正交时(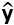 是y在col X上的正交投影),向量
是y在col X上的正交投影),向量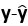 长度达到最短(由向量在向量空间上的正交投影的性质),因此
长度达到最短(由向量在向量空间上的正交投影的性质),因此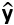 是向量y在X的列空间(col X)上的正交投影(反证法:假设
是向量y在X的列空间(col X)上的正交投影(反证法:假设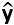 不是正交投影,则存在一个正交投影
不是正交投影,则存在一个正交投影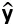 ‘使得
‘使得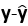 >
>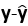 ‘,则
‘,则 长度不是最短的,故假设不成立)。
长度不是最短的,故假设不成立)。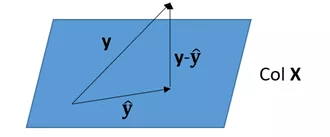
由之前的讨论,y在X的列空间上的正交投影满足方程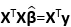 ,
,
求解该方程中的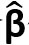 即可得到最小二乘直线的两个参数β0和β1 。
即可得到最小二乘直线的两个参数β0和β1 。
此外对于其他类型的曲线也可以进行类似的最小二乘拟合,例如拟合曲线y=β0+β1x+β2x2,只要使矩阵X=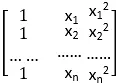 ,β=
,β=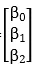 ,y=
,y=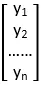 ,对方程
,对方程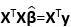 进行相同的求解即可。
进行相同的求解即可。
最小二乘法的应用
最小二乘法在数学建模及参数拟合的过程中有十分基础的应用。最小二乘法也常见于单细胞分析软件的底层算法,例如,2018年发表在Nature上的软件RNA velocity利用最小二乘法对模型中的参数γ进行了拟合[2]。
参考资料:
[1] 戴维 C.雷. 线性代数及其应用第四版.
[2] Gioele La Manno, S. L. RNA velocity of single cells[J]. Nature, 2018.