原文链接：https://blog.sciencenet.cn/blog-2970729-1112311.html
作者：luria的个人博客

这篇博文以简化的Needleman-Wunsch比对算法为例，详解比对算法的原理及代码实现。Needleman-Wunsch算法是最著名的全局比对算法，在此基础上形成的Smith-Waterman算法是最著名的局部比对算法，虽然两者都非常巧妙，但基本原理和代码相差不大，这里仅讲解Needleman-Wunsch算法。

1. Needleman-Wunsch算法的原理

1970年Saul B. Needleman and Christian D. Wunsch首次将动态规化的思路应用到生物信息学领域，形成了大名鼎鼎的Needleman-Wunsch算法，该算法在当前生物信息学领域得到广泛应用，是全局比对算法中最重要的算法。
闲言少述，直接进入正题。以下两条序列进行全局比对为例，Needleman-Wunsch算法的具体步骤如下：

sequence1 GCATGCU sequence2 GATTACA

1.1 初始化矩阵

首先建立一个空的矩阵，矩阵上的行名为sequence1的碱基，矩阵的列名为sequence2的碱基。因为需要初始值，所有数据区第一行和第一列依次为-1, -2, -3, -4…这组递减数列，相连两项之间的差值为gap罚分。
这里为了方便起见，采用最一般的罚分，即match得1分，mismatch和gap罚1分（即得-1分，以下叙述均用得分表示，若为罚分则得分为负）。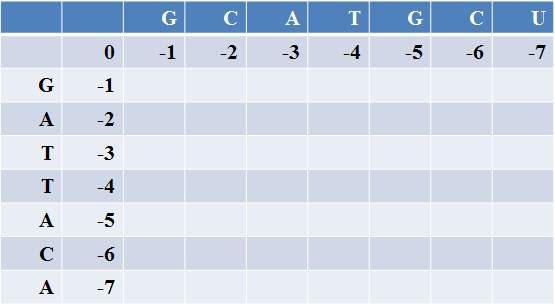
比对算法的原理及代码实现 - 图1
图1. 初始空矩阵
注：match=1, mismatch=-1, gap=-1

1.2 三个方向移动到当前位点时的综合得分

依次从左上往右下计算出每个位点的得分，计算时先算出从左，从上及从左上角移动到当前位点时的得分，这个得分值为：
不同方向移动综合得分 = 移动前位点的得分 + 移动过程的得分
移动前位点的得分为移动前位点方框中的值，移动过程的得分按1.1中的得分约定计算如下：
Ø 从上往下和从左往右移动时都会引入gap，前者是在横向这条序列上引入gap，后者是在纵向这条序列上引入gap，因此都会得-1分；
Ø 从左上往右下方向移动时，如果当前位点横向和纵向对应碱基一致，表明为match，得1分；如果当前位点横向和纵向对应碱基不一致，表明为mismatch，得-1分。

具体示意图如下：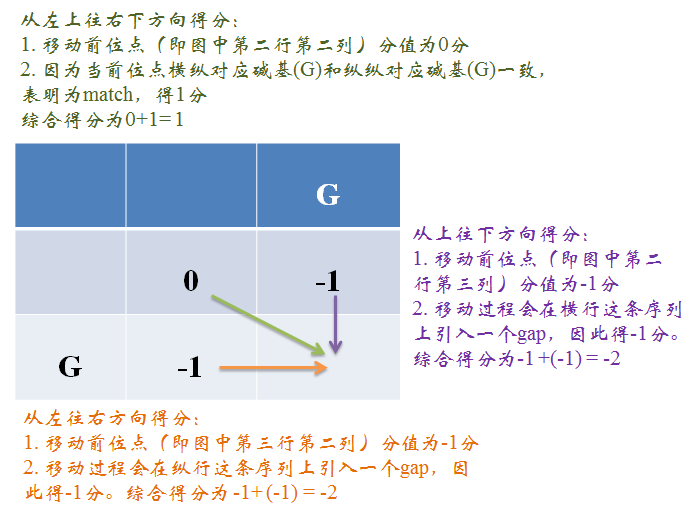
比对算法的原理及代码实现 - 图2
图2. 三个方向移动时综合得分
值得一提的是，Smith-Waterman算法[1]仅在此基础上加入一个0值，让上述三个方向上的值与0，共四个值比较大小。而且在最开始初始化矩阵时将初始行初始列的值都设为0。这样整个矩阵中的值没有负值。因此可以从任何位置开始，后面回溯时从矩阵中最大的值开始回溯，这样就可以达到局部比对的效果，真的是太精妙了！

1.3当前位点得分

从三个方向（从上到下，从左到右，从左上到右下）移动到当前位点的综合得分的最大值，即为当前位点得分。
那么由上图2中可得三个方向移动到当前位点时的最大得分为 max(1, -2, -2) = 1
即当前位点得分为1（图中表格第三行第三列值为1）

按照以上原则，将矩阵上每个位点都计算出来，填满整个表格。强列建议大家手动算一次，实际计算会让思路更加清晰，这对后面写代码实现非常有帮助！
我手动计算结果如下，与wiki百科[2]上的一致。
比对算法的原理及代码实现 - 图3
图3. 整个矩阵的结果图

1.4 回溯获取最佳比对结果

沿右下角向左上角回溯，每个位点依然有三个位置，左上，左边和上边，如果最大值出现在上面，则横向这条序列引入一个gap (“-“)，纵向这条序列取该处碱基；如果最大值出现在左边，则纵向这条序列引入一个gap (“-“)，横向这条序列取该处碱基; 如果最大值出现在左上角，则不引入gap，纵向和横向均取该处碱基。这样获取到两段序列，再反转过来（因为序列是从后往前回溯的）即为最终结果。
比对算法的原理及代码实现 - 图4
图4. 回溯找最佳路径

2. 用Python实现全局比对

方便起见，这里仅用了原生python实现算法，具体代码如下，有兴趣的朋友也可以使用cython或python数据分析包，或者其它语言实现，并欢迎贴到讨论区，谢谢。
——————————-
可下载代码源文件
global_alignment.py
——————————-

  1. #!/usr/bin/env python
  2. import sys 
  3. __author__  = 'luria@sohu.com'
  4. __date__    = '2018.05.04'
  5. __version__ = 'v1.0'
  7. def main(self, subject, query):
  8.     match, mismatch, gap = 1, -1, -1
  9.     # if you wanna to use other score matrix, 
  10.     # you could do code reactoring as a practice
  11.     pos_dict = {(i, j): 0 for i in xrange(len(subject)+1) for j in xrange(len(query)+1)}
  13.     for k in pos_dict:
  14.         if not k[0] and not k[1]: pos_dict[k] = 0
  15.         elif not k[0] and k[1]: pos_dict[k] = k[1] * gap
  16.         elif not k[1] and k[0]: pos_dict[k] = k[0] * gap
  17.     # print pos_dict
  19.     # this step must be follow first loop
  20.     for i in xrange(1, len(subject)+1):
  21.         for j in xrange(1, len(query)+1):   
  22.             up2down = pos_dict[(i-1, j)] + gap
  23.             left2right = pos_dict[(i, j-1)] + gap
  24.             if subject[i-1] == query[j-1]:
  25.                 topleft2bottomright = pos_dict[(i-1, j-1)] + match 
  26.             else:
  27.                 topleft2bottomright = pos_dict[(i-1, j-1)] + mismatch
  28.             pos_dict[(i, j)] = max(up2down, left2right, topleft2bottomright)
  30.     # print matrix
  31.     '''
  32.     for i in xrange(len(subject)+1):
  33.         temp = []
  34.         for j in xrange(len(query)+1):
  35.             temp.append(str(pos_dict[(i, j)]))
  36.         print "\t".join(temp)
  37.     '''
  39.     out_subject, out_query = '', ""
  40.     x, y = len(subject), len(query)
  41.     while 1:
  42.         if not x and not y: break
  43.         direct_dict = {      "up" : pos_dict[(x-1, y)],
  44.                            "left" : pos_dict[(x, y-1)],
  45.                        "top_left" : pos_dict[(x-1, y-1)]}
  46.       #print direct_dict
  47.         order = sorted(direct_dict.iteritems(), key=lambda o:o[1], reverse=True)
  48.         # only get one best path at this program, 
  49.         # you can get all best path if you like
  50.         if order[0][0] == "up":   
  51.             out_subject += "-"      
  52.             out_query += query[y-1]
  53.             x -= 1
  54.         elif order[0][0] == 'left': 
  55.             out_query += "-"
  56.             out_subject += subject[x-1]
  57.             y -= 1
  58.         else:
  59.             out_subject += subject[x-1]
  60.             out_query += query[y-1]
  61.             x -= 1
  62.             y -= 1      
  63.     print out_subject[::-1]
  64.     print "".join(["|" if out_subject[i]== out_query[i] else " " 
  65.                 for i in xrange(len(out_subject))][::-1])
  66.     print out_query[::-1]
  67.     print 
  68. if __name__ == '__main__':
  69.     if len(sys.argv) == 1:
  70.         sys.exit("[usage] global_align.py <subject> <query>")
  71.     main(*sys.argv)

参考材料：
[1] https://en.wikipedia.org/wiki/Smith-Waterman_algorithm
[2] https://en.wikipedia.org/wiki/Needleman-Wunsch_algorithm